Test environment

　　Ubuntu 18.04, gcc 8.4

 

Review the fast scheduling algorithm, only to get unexpected results. The example code is as follows

 1 #include <stdio.h>
 2 
 3 void mySwap(int *p, int *q)
 4 {
 5     *p ^= *q;
 6     *q ^= *p;
 7     *p ^= *q;
 8 }
 9 
10 void getPivot(int *srcArr, int left, int right)
11 {
12     int mid = left + (right-left)/2;
13 
14     if(srcArr[left] > srcArr[mid])
15     {
16         mySwap(&srcArr[left], &srcArr[mid]);
17     }
18 
19     if(srcArr[mid] > srcArr[right])
20     {
21         mySwap(&srcArr[mid], &srcArr[right]);
22     }
23 
24     if(srcArr[left] > srcArr[right])
25     {
26         mySwap(&srcArr[mid], &srcArr[right]);
27     }
28 }
29 
30 void quickSort(int *srcArr, int left, int right)
31 {
32     if (left >= right)
33     {
34         return;
35     }
36 
37     int low = left;
38     int high = right;
39 
40     int pivot;
41     //getPivot(srcArr, low, high);
42 
43     int mid = low + (high-low)/2;
44 
45     mySwap(&srcArr[low], &srcArr[mid]);
46 
47     pivot = srcArr[low];
48 
49     while (low < high)
50     {
51         while (srcArr[high] >= pivot && low < high)
52         {
53             --high;
54         }
55 
56         srcArr[low] = srcArr[high];
57 
58         while (srcArr[low] <= pivot && low < high)
59         {
60             ++low;
61         }
62 
63         srcArr[high] = srcArr[low];
64 
65     }
66 
67     srcArr[low] = pivot;
68     quickSort(srcArr, left, low-1);
69     quickSort(srcArr, low+1, right);
70 }
71 
72 int main()
73 {
74     int srcArr[10] = {1, 3, 5, 7, 9, 2, 4, 6, 8, 10};
75 
76     quickSort(srcArr, 0, 9);
77 
78     for(int i = 0;  i < 10; ++i)
79     {
80         printf("%d ", srcArr[i]);
81     }
82 
83     putchar(10);
84 
85     return 0;
86 }

The operation results are as follows

 

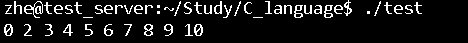
The first element is 0, which should be 1. In this process, I didn't modify the elements in the array. Why did 0 appear? Why is only the first element problematic? Why are the other elements OK?

 

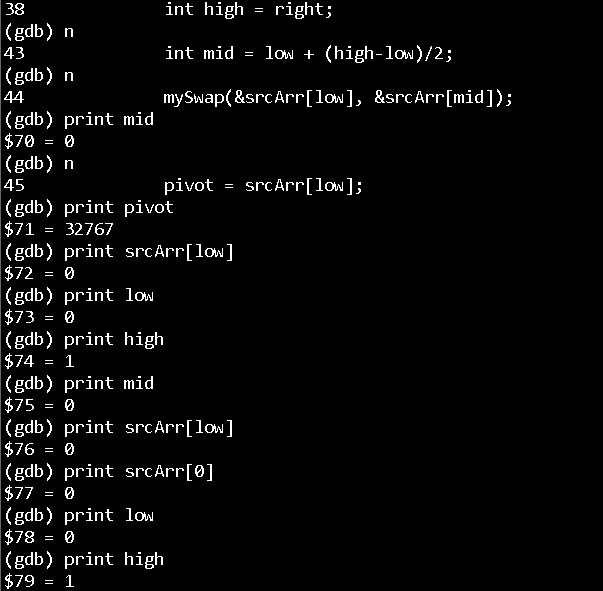
Using gdb debugging, when the sorted sequence is as close to the left as possible, the subscript and element values are printed, and an unexpected phenomenon is found. When sorting the sequence of elements 0 and 1, execute the code in line 44 (exchanging the values of the two elements) in the screenshot, and there is no problem with the subscript, low = 0, mid = 0, high = 1.

The problem is that the value of the 0th element becomes 0. It's just an exchange. How does the 0th element become 0? Let's see that the exchange of the values of two elements is carried out through XOR. It suddenly reacts. It is estimated that it is XOR with itself. Any integer is XOR with itself and the result is 0.

(please know that the line number in the screenshot is a little different from that in the previous example code)

 

Adjustment: judge whether it is the same element before exchange, and exchange for different elements.

1 if (low != mid)
2 {
3     mySwap(&srcArr[low], &srcArr[mid]);
4 }

Run again

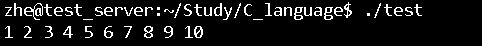
The results are in line with expectations.

 

Back to this question, why is only the first element problematic? Why are the other elements OK?

According to the data in the array provided above, the next sorting process is repeated. In the sorting process, there is only one element on the right side of the sequence on both sides of the central axis (the element on the left is smaller than the central axis, and the element on the right is larger than the central axis). In the last few rounds, there is just one round of four elements, that is, the 0th to 3rd elements. After sorting, there are two elements left on the left of the central axis, that is, after 0 and the first element, there is only the third element left on the right of the central axis.

The sequences of these two elements are exchanged before sorting. I want to take the middle element as the central axis as far as possible (assuming that the middle element is the mean value), so I exchange the leftmost element with the element in the middle of the sequence. Note that at this time, the middle element is consistent with the subscript of the 0th element, that is, the middle element is the 0th element. The same element XOR, the result is 0, and the result makes the value of the 0th element 0.

This also led to problems.

 

The disadvantage of quick sorting is also obvious in the process of redoing. If the value of the central axis is not obtained well, as in the example code, there is always only one element on one side of the central axis, resulting in the worst case and the worst time complexity. It is worth thinking about taking the appropriate value of the central axis. Obtaining a good intermediate value can make the sequence distribution of the central axis more uniform and highlight the advantages of fast scheduling. First, a random algorithm can be used to obtain a random subscript, but it can not guarantee that it must be optimal. In addition, the random algorithm also needs some overhead. Second, take the middle of the first element, the middle element and the tail element as the middle element (that is, compare the size of the three to take the middle element), which also requires at least three elements in the sequence. Of course, this is also spelling out personality. There is no guarantee that the central axis value is the most reasonable.

The following example code implements the second method by adding judgment conditions to ensure that there are at least three elements in the sequence.

 1         int low = left;
 2         int high = right;
 3         int center = (left+right)/2;
 4         int pivot;
 5 
 6         if(right - left >= 2)
 7         {
 8             if(arr[left] > arr[right])
 9             {
10                 mySwap(&arr[left], &arr[right]);
11             }
12 
13             if(arr[center] > arr[right])
14             {
15                 mySwap(&arr[center], &arr[right]);
16             }
17 
18             if(arr[left] > arr[center])
19             {
20                 mySwap(&arr[left], &arr[center]);
21             }
22 
23             mySwap(&arr[left], &arr[center]);
24         }
25 
26         pivot = arr[left];            

 

Add an aside. If the number of elements is small (e.g. less than 20), you can choose other sorting algorithms, such as insertion sorting. The above example code is only for reviewing the quick sort algorithm.

Note: because the bug reappears later, there is an error within 3 lines between the code line number in the debugging of the screenshot and the line number in the sample code. Please know.

 

Reference materials:

Data structure and algorithm analysis, C language implementation, mark Alan Weiss