Day5

T1 matrix (※ difference)

Application of difference technique in interval operation.
For a sequence { a i } \{a_i\} {ai}, if we are in [ l , r ] [l,r] All elements of the [l,r] interval are increased s s s. We can consider O ( 1 ) O(1) O(1) record the operation. New sequence { b i } \{b_i\} {bi} initially all elements are 0 0 0, record after an interval operation b l ← b l + s , b r + 1 ← b r + 1 − s b_l\leftarrow b_l + s,b_{r+1}\leftarrow b_{r+1}-s bl ← bl + s,br+1 ← br+1 − S. if there are several operations, do the same as above. Finally, ask the sequence after the operation { a i ′ } \{a'_i\} {ai ′}, then yes { b i } \{b_i\} {bi} do a prefix and get { b i ′ } \{b'_i\} {bi ′}, there is a i ′ = a i + b i ′ a'_i=a_i+b'_i ai′​=ai​+bi′​.
Differential can efficiently solve the problem of "multiple interval operations, and finally single query". The steps are summarized as follows:

1. Open a differential array b [] for each receive operation [ l , r ] + s [l,r]+s [l,r]+s, then B [l] + = s, B [R + 1] - = s
2. In the final query, prefix and operate the differential array first. bs[i] = bs[i-1] + b[i]
3. Finally, the answer is ans[i] = a[i] + bs[i]

Back to this question, of course, we can consider the number of pieces per operation r ′ r' r ', and then mark each line, but the complexity increases with the number of queries q q q is too large when it is relatively large, so we should consider improving this O ( n q ) O(nq) O(nq).
Consider the process of the above algorithm, as shown in the following figure:

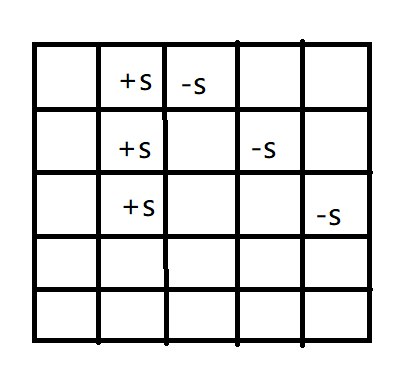
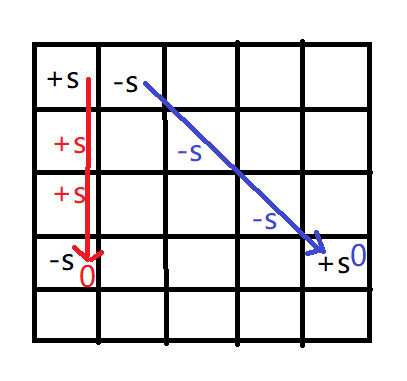
We find that interval operations also occur in the longitudinal direction, so it is obvious that we can consider differentiating the existing difference markers in the longitudinal direction. The operation of longitudinal difference for the existing difference group b1 [] [] is relatively simple, but the operation of oblique difference is not obvious. However, we can still consider setting a new oblique difference array b2 [] []. When calculating the final table, we first sum up the b1 [] [] longitudinal difference prefix, and then sum up the b1 [] [] transverse difference prefix, Finally, the oblique prefix sum of the oblique difference group b2 [] [] is processed, and all the difference arrays are added to obtain the element at a certain position.

#include<iostream>
#include<cstdio>

using namespace std;
typedef long long ll;
int n,q,row,col,len,sum;
ll map[2005][2005],tmp,ans;
ll tag[2005][2005],ttag[2005][2005];


int main()
{
	scanf("%d%d",&n,&q);
	for(int t = 1;t <= q;t ++)
	{
		scanf("%d%d%d%d",&row,&col,&len,&sum);
		tag[row][col] += sum;
		ttag[row][col+1] -= sum;
		tag[min(row+len,n+1)][col] -= sum;
		ttag[min(n+1,row+len)][min(col+len+1,n+1)] += sum;
	}
	
	for(int i = 1;i <= n;i ++)
	{
		tmp = 0;
		for(int j = 1;j <= n;j ++)
		{
			tmp += tag[i][j] + ttag[i][j];
			map[i][j] = tmp;
			tag[i + 1][j] += tag[i][j];
			ttag[i + 1][j + 1] += ttag[i][j];
		}
	}
	for(int i = 1;i <= n;i ++)
		for(int j = 1;j <= n;j ++)
			ans = ans^map[i][j];
	printf("%lld",ans);
	return 0;
}

Day6

T1 travel (※ difference, tree dichotomy and multiplication)

This topic can be summarized as "node coverage problem on tree". It has the characteristics of multiple operations and single final query. Differential can be considered. The specific operations are as follows:

1. For each point i i i find the farthest ancestor it can jump up j j j
2. set up i i i's father is fa ⁡ ( i ) \operatorname {fa}(i) fa(i), differential marker b[fa(i)] ++,b[fa(j)]++
3. Finally, the answer is traced back from the leaf node to the root node, and in the process bs ⁡ ( u ) = ∑ i ∈ { son ⁡ ( u ) } bs ⁡ ( i ) \operatorname{bs}(u) = \sum_{i\in \{\operatorname{son}(u)\}}\operatorname{bs}(i) bs(u) = Σ I ∈ {son(u)} bs(i), that is, bs[u] += bs[son[u][i]]

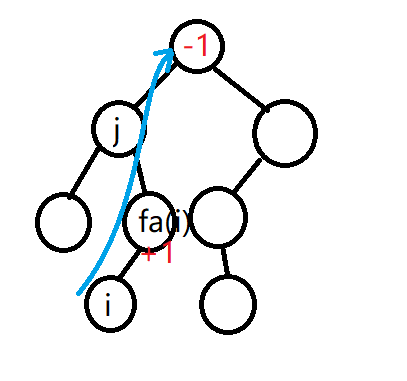
As for the up jump process, the preprocessing ancestor and the distance between ancestors can be doubled.

#include<iostream>
#include<cstdio>

using namespace std;
typedef long long ll;
int n;
ll d[200005],y;
int x,head[200005],cnt;
int f[200005][25];
ll di[200005][25];
int ans[200005];
struct edge{
	int nxt;
	int to;
	ll dis;
}e[500005];

void prework(int u,int fa)
{
	for(int i = 1;i <= 20;i ++)
	{
		f[u][i] = f[f[u][i-1]][i-1];
		di[u][i] = di[u][i-1]+di[f[u][i-1]][i-1];
	}
	int v = 0;
	for(int i = head[u];i;i = e[i].nxt)
	{
		v = e[i].to;
		if(v == fa) continue;
		f[v][0] = u;di[v][0] = e[i].dis;
		prework(v,u);
	}
	return ;
}

void addedge(int from,int to,ll dis)
{
	cnt ++;
	e[cnt].nxt = head[from];
	e[cnt].to = to;
	e[cnt].dis = dis;
	head[from] = cnt;
	cnt ++;
	e[cnt].nxt = head[to];
	e[cnt].to = from;
	e[cnt].dis = dis;
	head[to] = cnt;
	return ;
}

void dfs(int u)
{
	if(u > 1 && d[u] >= di[u][0])
	{
		int x = u;int tmp = 0;
		for(int i = 20;i >= 0;i --)
		{
			if(tmp + di[x][i] <= d[u])
			{
				tmp += di[x][i];
				x = f[x][i];
			}
		}
		ans[f[u][0]] ++;ans[f[x][0]] --;
	}
	
	for(int i = head[u];i;i = e[i].nxt)
	{
		if(f[u][0] != e[i].to)
		{
			dfs(e[i].to);
			ans[u] += ans[e[i].to];
		}
	}
	return ;
}

int main()
{
	scanf("%d",&n);
	for(int i = 1;i <= n;i ++)
		scanf("%lld",&d[i]);
	for(int i = 2;i <= n;i ++)
	{
		scanf("%d%lld",&x,&y);
		addedge(i,x,y);
	}
	prework(1,0);
	dfs(1);
	for(int i = 1;i <= n;i ++)
		printf("%d\n",ans[i]);
	return 0;
}