Title portal
Title Description
One N × M N\times M N × Matrix of M A A A completely by 0 0 0 and 1 1 1 consists of two numbers( 0 < N , M ≤ 8 0<N,M\le8 0 < n, m ≤ 8), matrix No i i Line i j j The item on column j is A i , j A_{i,j} Ai,j​， i i i and j j j from 0 0 0, i.e 0 ≤ i < N 0\le i<N 0≤i<N， 0 < = j < M 0<=j<M 0<=j<M. There are now two operations:
(1) Any item in the matrix A i , j A_{i,j} Ai,j ， changed to number 1 1 1；
(2) Any item in the matrix A i , j A_{i,j} Ai,j ， changed to number 0 0 0；
Now give the initial matrix A A A. A minimum of operations are required to make the matrix A A At least in A R o w C o u n t RowCount RowCount line is palindrome, and at least C o l u m C o u n t ColumCount The ColumCount column is the of palindromes. Output the minimum number of operations.
The r-th line in the matrix is palindrome, which refers to the sequence A r , 0 , A r , 1 , ⋅ ⋅ ⋅ , A r , M − 1 {A_{r,0},A_{r,1},···,A_{r,M-1}} Ar,0, Ar,1, ⋅⋅⋅, Ar,M − 1 palindromes, that is, all palindromes i i i yes A r , i = A r , M − 1 − i A_{r,i}=A_{r,M-1-i} Ar,i​=Ar,M−1−i​；
Column c in the matrix is palindrome, which refers to the sequence A 0 , c , A 1 , c , . . . A N − 1 , c {A_{0,c},A_{1,c},...A_{N-1,c}} A0,c​,A1,c​,... AN − 1,c palindromes, i.e. all i i i yes A i , c = A N − 1 − i , c A_{i,c}=A_{N-1-i,c} Ai,c​=AN−1−i,c​.

for example 4 × 4 4\times4 four × The matrix of 4 is as follows:

0000
1000
1100
1110

requirement R o w C o u n t = 2 RowCount=2 RowCount=2, and C o l u m C o u n t = 2 ColumCount=2 ColumCount=2.
Can A 3 , 0 A_{3,0} A3,0 changed to 0 0 0, make the second 0 0 Line 0 and 3 3 3 lines of palindromes, at the same time 0 0 Columns 0 and 3 3 3 palindromes. The changes are as follows:

0000
1000
1100
0110

Input format
The first line is two positive integers, representing R o w C o u n t RowCount RowCount， C o l u m C o u n t ColumCount Columbcount, and 0 ≤ R o w C o u n t ≤ N 0\le RowCount\le N 0≤RowCount≤N， 0 ≤ C o l u m C o u n t ≤ M 0\le ColumCount\le M 0≤ColumCount≤M.
The second line is an integer N N N. That is, the number of rows of the matrix, 1 ≤ N ≤ 8 1\le N\le 8 1≤N≤8.
After that N N N rows, one for each row M M M 0 \texttt{0} 0, 1 \texttt{1} A string of 1 characters, representing N × M N\times M N × Information of M matrix.

Output format
An integer representing the minimum number of operations.

sample input

2 2
4
0000
1000
1100
1110

sample output

1

For this problem, after all N , M N,M N. M only 8 8 8, so we can take

Violence!

First from N N Enumeration in N rows R o w C o u n t RowCount RowCount line, from M M Enumeration in row M C o l o m C o u n t ColomCount Colorcount line. This can be solved by deep search. Then calculate the minimum number of steps to turn these columns into palindromes.
When calculating rows, consider the aftereffect and enumerate a point. If the column where this point is located is also selected, the corresponding point of this point in this column should also be taken into account. If this point is also selected in the column where the corresponding point of the row is located, its corresponding point in that column should also be taken into account.
Don't you talk?
Combined with the diagram, it can be better understood.

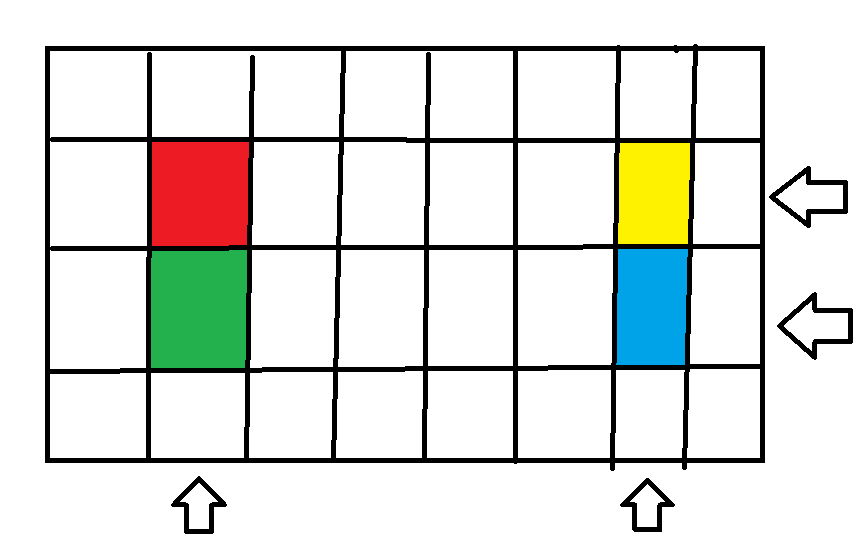
One 4 × 8 4\times8 four × 8, where
Red point: the point selected during enumeration;
Green Point: this point is in the corresponding point of this column;
Yellow point: this point is at the corresponding point of this line;
Blue point: the corresponding point of this point in this row is the corresponding point of its column;
The arrows refer to the selected rows and columns.
Place the four points in 1 1 1 number of and 0 0 The number of 0 is counted, and the minority obeys the majority. No aftereffect can be guaranteed.
Same as.
The code is as follows.

#include<bits/stdc++.h>
using namespace std;
int rc,cc,n,m,ans=0x7fffffff;
char s[10][10],s2[10][10];//s is the original matrix and s2 is the matrix to be modified
int r[10],c[10];//Selected rows and columns
bool ru[10],cu[10];//Are rows and columns selected
void count()
{
	int tot=0;
	memcpy(s2,s,sizeof(s2));
	for(int i=1;i<=rc;i++)
		for(int j=1;j<=m/2;j++)//Calculate selected rows
			if(s2[r[i]][j]!=s2[r[i]][m-j+1])//Different characters
			{
				int a=1,b=1;//a is the quantity of 0 and b is the quantity of 1
				if(cu[j])//The column is selected
				{
					if(s2[n-r[i]+1][j]=='0') a++;//Judge the corresponding point of the column
					else b++;
				}
				if(cu[m-j+1])//The column of the corresponding point is selected
				{
					if(s2[n-r[i]+1][m-j+1]=='0') a++;//Calculate the corresponding point in the column where the corresponding point is located
					else b++;
				}
				if(a>b)//More than 0, all changed to 0
				{
					s2[r[i]][j]='0';
					s2[r[i]][m-j+1]='0';
					if(cu[j]) s2[n-r[i]+1][j]='0';
					if(cu[m-j+1]) s2[n-r[i]+1][m-j+1]='0';
					tot+=b;//Cumulative modified quantity
				}
				else//ditto
				{
					s2[r[i]][j]='1';
					s2[r[i]][m-j+1]='1';
					if(cu[j]) s2[n-r[i]+1][j]='1';
					if(cu[m-j+1]) s2[n-r[i]+1][m-j+1]='1';
					tot+=a;
				}
			}
	for(int j=1;j<=cc;j++)//ditto
		for(int i=1;i<=n/2;i++)
			if(s2[i][c[j]]!=s2[n-i+1][c[j]])
			{
				int a=1,b=1;
				if(ru[i])
				{
					if(s2[i][m-c[j]+1]=='0') a++;
					else b++;
				}
				if(ru[n-i+1])
				{
					if(s2[n-i+1][m-c[j]+1]=='0') a++;
					else b++;
				}
				if(a>b)
				{
					s2[i][c[j]]='0';
					s2[n-i+1][c[j]]='0';
					if(ru[i]) s2[i][m-c[j]+1]='0';
					if(ru[n-i+1]) s2[n-i+1][m-c[j]+1]='0';
					tot+=b;
				}
				else
				{
					s2[i][c[j]]='1';
					s2[n-i+1][c[j]]='1';
					if(ru[i]) s2[i][m-c[j]+1]='1';
					if(ru[n-i+1]) s2[n-i+1][m-c[j]+1]='1';
					tot+=a;
				}
			}
	ans=min(ans,tot);
}
void col(int k)//dfs enumeration column
{
	if(k==cc+1) count();
	else for(int i=c[k-1]+1;i<=m;i++)
	{
		c[k]=i;
		cu[i]=true;
		col(k+1);
		cu[i]=false;
	}
}
void row(int k)//dfs held
{
	if(k==rc+1) col(1);
	else for(int i=r[k-1]+1;i<=n;i++)
	{
		r[k]=i;
		ru[i]=true;
		row(k+1);
		ru[i]=false;
	}
}
int main()
{
	scanf("%d%d%d%s",&rc,&cc,&n,s[1]+1);
	m=strlen(s[1]+1);
	for(int i=2;i<=n;i++) scanf("%s",s[i]+1);
	row(1);
	printf("%d",ans);
	return 0;
}