Solution of ECJTU ACM level 21 trial

Game link
Note: the following order is the expected difficulty order

1. The Chinese don't lie to the Chinese

tag: Escape Character

Output directly. Pay attention to the escape of the character \
Reference code:

#include <stdio.h>
int main(){
    printf("I Love ecjtuacm /\\=/\\")
return 0;
}

C. Happy New Year

tag: Reading Comprehension

After carefully reading the meaning of the question, you can always get the maximum points, and the points do not exist in the same situation. So the answer is n − 1 n-1 n−1
Reference code:

#include <stdio.h>
int main(){
    int n; 
	while(~scanf("%d", &n)) {
        int x;for(int i = 1; i <= n; ++ i) scanf("%d", &x);
        printf("%d\n", n - 1);
    }
    return 0;
}

K. An Acmer looking for love

tag: string processing

Find out the relative position of 3. In particular, the original position of the first 3 is how much (the string subscript starts from 1). First find the first 3, and then record the location of the last 3. Exit after 8 outputs
Reference code:

#include <stdio.h>
#include <string.h>
char s[330];

int main()
{
    int n;
    scanf("%d", &n);
    while(n --) {
        scanf("%s", s + 1); // Subscript starts with 1
        int len = strlen(s + 1);
        int pre = 0, cnt = 0; // The position of the last 3, the number of outputs
        for(int i = 1; i <= len; ++ i) {
            if(s[i] == '3') {
                if(pre == 0) printf("%d", i);
                else printf("%d", i - pre);
                pre = i;
                cnt ++;
                if(cnt == 8) break;
            }
        }
        printf("\n");
    }
    return 0;
}

F. Brother Zhao who loves teaching

tag: structure, sorting

We can use structures to store information (of course, only arrays can be used, as long as you don't faint). Then get a new ranking according to the results, record the following progress and retrogression (don't care if you don't advance or retreat), and finally output as required. This question can be sorted by sort or by bubbling (sorted according to grades) in class. Specific reference code:

#include <stdio.h>
struct student{
    int pre, grade, now, dex; // Previous ranking, current performance, current ranking
};
student a[22];
int main()
{
    int t; scanf("%d", &t);
    while(t -- ) {
        int n; scanf("%d", &n);
        for(int i = 1; i <= n; ++ i) {
            scanf("%d", &a[i].grade);
            a[i].pre = i; // The previous ranking is order
        }
        // Next sort
        for(int i = 1; i <= n; ++ i) {
            for(int j = i + 1; j <= n; ++ j) {
                if(a[i].grade < a[j].grade) {
                    student t = a[i];
                    a[i] = a[j];
                    a[j] = t;
                }
            }
        }// Record the following progress and setbacks
        for(int i = 1; i <= n; ++ i) {
            a[i].now = i;
            a[i].dex = a[i].pre - a[i].now;
        }// Then back in the original order
        for(int i = 1; i <= n; ++ i) {
            for(int j = i + 1; j <= n; ++ j) {
                if(a[i].pre > a[j].pre) {
                    student t = a[i];
                    a[i] = a[j];
                    a[j] = t;
                }
            }
        }        
        int add = 0, del = 0;// Here is the direct output result
        for(int i = 1; i <= n; ++ i) {
            printf("%d ", a[i].dex);
            if(a[i].dex > 0) add++;
            else if(a[i].dex < 0) del ++;
        }
        printf("\n%d %d\n", del, add);
    }
    return 0;
}

A. Simple questions

tag: high precision, two points

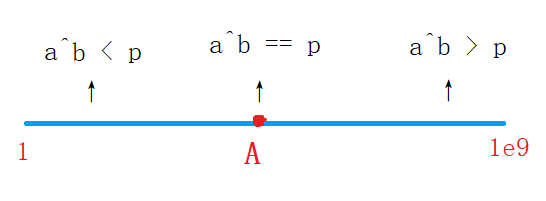
We know b , p b,p b,p . We can use a line segment a a a. Then there is a point on this line segment (the point in the figure below) A A A) Make a b = = p a^b == p AB = = P (the problem has guaranteed that the data has a solution), then the left side of this point is a b < p a^b < p AB < p, with edge a b > p a^b > p AB > P, which is the figure below. How can we efficiently solve the points in the graph A A A. The answer is two. as for a b a^b ab will exceed any type of range, and we can use high-precision solution.

Reference code:

#include <stdio.h>
#include <string.h>
#define ll long long
#define N 1010
ll b, a[N], len;
char p[N];

void init() {
    len = 1;
    a[0] = 1;
}

void mul(ll b) {
    for(ll i = 0; i < len; ++ i) a[i] *= b;
    ll cf = 0;
    for(ll i = 0, t = 0; i < len; ++ i) {
        t = a[i] + cf;
        a[i] = t % 10;
        cf = t / 10;
    }
    while(cf) a[len ++] = cf % 10, cf /= 10;
}

void a_b(ll _a, ll _b) {
    init();
    for(ll i = 0; i < _b; ++ i) 
        mul(_a);
}

int cmp(ll *a, char *p) {
    int lp = strlen(p);
    if(len > lp) return 1;
    if(len < lp) return -1;
    for(int i = len - 1; i >= 0; -- i) {
        if(a[i] > p[len - i - 1] - '0') return 1;
        else if(a[i] < p[len - i - 1] - '0') return -1;
    }
    return 1;
}

int main()
{
    while(scanf("%lld%s", &b, p) != EOF)
    {
        // Dichotomy: divide the interval [l, r] into [l, mid], [mid + 1, r]
        ll l = 1, r = 1e9;
        while(l < r) {
            ll mid = l + r >> 1;
            a_b(mid, b);// Find a^b
            if(cmp(a, p) == 1) r = mid;
            else l = mid + 1;
        }
        printf("%lld\n", l);
    }
}

E. Character compression

tag: C++ STL string problem

Locate simple questions without too much explanation. See code for details:

#include <bits/stdc++.h>

using namespace std;


string work(string str) //Unzip the string str and return the unzipped result
{
	string res = "", word = "";

	for(int i = 0; i < str.length(); i ++)
	{
		if('a' <= str[i] && str[i] <= 'z')	word += str[i]; //It's a letter
		else //It's a number
		{
			int number = 0;
			int j = i;
			while('0' <= str[j] && str[j] <= '9')	
			{
				number = number * 10 + str[j] - '0';	
				j ++;			
			}
			i = j - 1;

			while(number --)	res += word; //Add number word s
			word = ""; //Note that every time you empty word
		}
	}
	return res;
}

int main()
{
	string a, b;
	cin >> a >> b;
	//Unzip a and b
	a = work(a);
	b = work(b);

	/*
	You can use the string's own function find()
	The following a.find(b) is to find out whether B exists in a
	If string::npos is not returned, it is generally - 1
	If found, returns the subscript of the first character of b when it first appears in a
	*/
	if(a == b)	puts("A=B");
	else if(a.find(b) != -1)	puts("A>B");
	else if(b.find(a) != -1)	puts("A<B");
	else	puts("A!=B");

	return 0;
}

A. Check in question

tag: greedy

First, don't be frightened by him, QAQ. Then, let's analyze the problem. We're going to n n n individuals are grouped, and the combat effectiveness after grouping is m i n ( a 1 , ⋅ ⋅ ⋅ ， a x ) ∗ x min(a_1, ···，a_x) * x min(a1, ⋅⋅⋅⋅, ax) * x we should make the number of groups as large as possible. Then, if we group from small to large, according to the calculation formula of combat effectiveness, we will find that it will only drag down those with strong combat effectiveness later. Therefore, we should group from large to small. In addition, pay attention to the data range of this problem (remember to open it) l o n g l o n g long long longlong)
Reference code:

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL a[N];
bool cmp(LL a, LL b) {
	return a > b;
}

int main()
{
	int T; cin >> T; // Group T Data
	while(T -- ) {
		int n;
		LL m;
		cin >> n >> m;
		for(int i = 1; i <= n; ++i ) cin >> a[i];
		sort(a + 1, a + 1 + n, cmp); // Sort from large to small
		LL res = 0, now = 0, cnt = 0;// grouping
		for(int i = 1; i <= n; ++ i) {
			if(now == 0) now += a[i], ++ cnt;
			else {
				++ cnt;
				now = a[i] * cnt;
			}
			if(now >= m) ++ res, now = cnt = 0;
		}
		cout << res << "\n";
	}
	return 0;
}

D. Save Fanfan

tag: simulation

Topic: you have to make complaints about this question. Although you just think of a simple simulation, it is difficult to change it by diudiu. Though this problem is only a little clearer than other questions, it needs to be clear. It is good to read the code directly. The main thing is to pay attention to the data range, and use longlong to consider clearly fifty. For the two special cases of 100 and 20 and 10 and 2, only the number of sheets plus one at least, but the number of sheets plus three is required for 50 and 5. Therefore, it is necessary to determine whether there is a better solution when 5 or 50 exists (you can not disassemble 50 and 5) In addition, it is necessary to start from the large ones and try not to tear down smaller denominations, so you need to pay attention to this (actually very satisfied). Pay attention to the 170 (that's what I mean) given in my sample. Look at the code for other details. It is mainly to test the details. You can make it as long as it is fine enough. It's good to do it more if times. The problem solution uses a container, and you use an array.

#include<bits/stdc++.h>
using namespace std;

int a[8]={100,50,20,10,5,2,1};

void solve(){
    long long n;cin>>n;
    long long cnt=0;
    vector<long long>ans;
    for(int i=0;i<7;i++){
        long long x = n/a[i];
        cnt+=x;
        ans.push_back(x);
        n%=a[i];
    }
    if(cnt&1){
        if(ans[4] && ans[6]){//There are five and one
            ans[4]-=1;
            ans[6]-=1;
            ans[5]+=3;
            cnt+=1;
        }
        else if(ans[1] && ans[3]){//There are 50 and 10
            ans[1]-=1;
            ans[3]-=1;
            ans[2]+=3;
            cnt+=1;
        }
        else if(ans[0]){//100
            ans[0]-=1;
            ans[1]+=2;
            cnt+=1;
        }
        else if(ans[2]){//20
            ans[2]-=1;
            ans[3]+=2;
            cnt+=1;
        }
        else if(ans[3]){//10
            ans[3]-=1;
            ans[4]+=2;
            cnt+=1;
        }
        else if(ans[5]){//2
            ans[5]-=1;
            ans[6]+=2;
            cnt+=1;
        }
        else if(ans[1]){
            ans[1]-=1;
            ans[2]+=1;
            ans[3]+=3;
            cnt+=3;
        }
        else if(ans[4]){
            ans[4]-=1;
            ans[5]+=1;
            ans[6]+=3;
            cnt+=3;
        }
    }
    cout<<cnt;
    for(auto e : ans) cout<<" "<<e;
    cout<<"\n";
}
int main(){
    int t;
    cin>>t;
    while(t--){
        solve();
    }
    return 0;
}

J. Brother Yang's acm Road

tag: dynamic programming

If the restriction of "return when learning value is reduced to zero" in the meaning of the question is removed
We consider dp:
Status indication: f [ i ] [ j ] f[i][j] f[i][j] indicates from ( 1 , 1 ) (1, 1) (1,1)-> ( i , j ) (i, j) Maximum learning value of (i,j)
State calculation: we found that ( i , j ) (i,j) (i,j) only ( i − 1 , j ) o r ( i , j − 1 ) (i-1,j) or (i, j - 1) (i − 1,j)or(i,j − 1) take the maximum value, that is: f [ i ] [ j ] + = m a x ( f [ i − 1 ] [ j ] , f [ i ] [ j − 1 ] ) f[i][j] += max(f[i-1][j], f[i][j-1]) f[i][j]+=max(f[i−1][j],f[i][j−1])
Let's look at the key of this problem. If the learning value is zero, it will return. That is to say, we can go down only when the learning value of the current state is non-zero. Let's add a judgment in the dp process
Reference code:

#include <bits/stdc++.h>
const int N = 2020;
int dp[N][N], a[N][N];
bool vis[N][N];

void solve()
{
    int n, m;
    cin >> n >> m;
    mem(dp, 0); mem(a, 0); mem(vis, 0); // initialization
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j)
            cin >> a[i][j]; // read in data
    dp[1][1] = a[1][1] + 100; // starting point
    if(dp[1][1] <= 0) { // Die before you leave the school
        cout << "NO\n";
        return ;
    }
    vis[1][1] = true; // (1, 1) can you go on
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j)
        { // If the previous state can go on, then the state transition can be carried out
            if(vis[i - 1][j] && a[i][j] + dp[i - 1][j] > 0)
            {
                vis[i][j] = true;
                dp[i][j] = max(dp[i][j], a[i][j] + dp[i - 1][j]);
            }
            if(vis[i][j - 1] && a[i][j] + dp[i][j - 1] > 0)
            {
                vis[i][j] = true;
                dp[i][j] = max(dp[i][j], a[i][j] + dp[i][j - 1]);
            }
        }    
    if(vis[n][m] && dp[n][m] > 0) // If the final number is negative, it won't work
        cout << dp[n][m] << endl;
    else 
        cout << "NO\n";
}
int  main() {
    int T; cin >> T;
    while(T --) solve();
    return 0;
}

G. Square of melon boss

tag: thinking questions

If the inquired number itself is a square number, output it directly 1 1 1.

Otherwise:

If the number is odd, set the number to o d d = 2 x + 1 odd=2x+1 odd=2x+1，

There must be o d d = ( x + 1 ) 2 − x 2 odd = (x+1)^2-x^2 odd=(x+1)2−x2

If the number is even, set the number to e v e n even even, then it at least uses 3 3 Three squares can be expressed, that is, let e v e n even even minus 1 becomes an odd number, and then there is:

e v e n = 1 2 + o d d even=1^2+odd even=12+odd and o d d = ( x + 1 ) 2 − x 2 odd=(x+1)^2-x^2 odd=(x+1)2−x2

e v e n = 1 2 + ( x + 1 ) 2 − x 2 even=1^2+(x+1)^2-x^2 even=12+(x+1)2−x2

As for whether you can use two square numbers, you can make a table and preprocess all the numbers that can only be expressed by two square numbers in advance.

Time complexity O ( n ) O(n) O(n)
Reference code:

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int cnt, arr[N];
int ans[N];

int main()
{
	//Find all the squares, 1e6 within 1000
	for(int i = 1; ; i ++)
	{
		int t = i * i;
		if(t > 1000000)	break; //Greater than 1e6 stop
		//Store t in array
		arr[cnt ++] = t;
		ans[t] = 1; //Marked square ans=1
	}

	for(int i = 0; i < cnt; i ++)
		for(int j = 0; j < cnt; j ++)
        {
            int t1 = arr[i] + arr[j];
            int t2 = arr[i] - arr[j];
			//The number of queries is a positive integer in the range of [1,1e6]
            if(0 < t1 && t1 <= 1000000 && !ans[t1])    ans[t1] = 2;
            if(0 < t2 && t2 <= 1000000 && !ans[t2])    ans[t2] = 2;
        }


	int q; scanf("%d", &q);
	while (q --)
	{
		int x;
		scanf("%d", &x);
		if(ans[x])	printf("%d\n", ans[x]); //If x is marked before, ans[x] will be output directly
		else	printf("3\n"); //Otherwise, it's 3
	}

	return 0;
}

H. I often kill him alone

tag: BFS

Idea 1:

Because we can break a wall (that is, 1), and we don't know which one is the best. The intuitive idea is to enumerate each 1 violently, find the time when the 1 is broken, and then take a minimum value in all cases. (naturally, this method will time out
Reference code:

#include <bits/stdc++.h>

using namespace std;

const int N = 510;

struct Node {int x, y;};
int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};

int n, m, t;
int tx, ty, fx, fy;
char g[N][N];
int d[N][N];

void bfs()
{
	for(int i = 0; i < n; i ++)
		for(int j = 0; j < m; j ++)	d[i][j] = -1;
	
	queue<Node> q;
	q.push({tx, ty}), d[tx][ty] = 0;

	while(!q.empty())
	{
		Node u = q.front();
		q.pop();

		for(int i = 0; i < 4; i ++)
		{
			int nx = u.x + dx[i], ny = u.y + dy[i];
			if(nx < 0 || nx >= n || ny < 0 || ny >= m || g[nx][ny] == '1')	continue;
            if(d[nx][ny] != -1)	continue;//Has been visited
			d[nx][ny] = d[u.x][u.y] + 1;
            
			q.push({nx, ny});
		}
	}
}

int main()
{
	scanf("%d%d%d", &n, &m, &t);
	for(int i = 0; i < n; i ++)	scanf("%s", g[i]);

	for(int i = 0; i < n; i ++)
		for(int j = 0; j < m; j ++)
		{
			if(g[i][j] == 'T')	tx = i, ty = j, g[i][j] = '0';
			if(g[i][j] == 'F')	fx = i, fy = j, g[i][j] = '0';	
		}
	
    bfs();
	int ans;
	if(d[fx][fy] == -1) ans = 1e8;
	else    ans = d[fx][fy];
	
	for(int i = 0; i < n; i ++)
		for(int j = 0; j < m; j ++)
			if(g[i][j] == '1')
			{
				g[i][j] = '0';
				bfs();
				g[i][j] = '1';
				if(d[fx][fy] != -1)	ans = min(ans, d[fx][fy]);
				
			}
	
	if(ans <= t)	printf("YES\n%d\n", ans);
	else	printf("NO\n");

	return 0;
}

Idea 2:

With the above thinking, we can think about how to optimize without violence enumerating each wall.

First, if t can break a wall to reach f, it means that it can traverse the position of the wall from T and the position of the wall from F.

Therefore, we can only achieve the goal by bfs twice. For the first time, we traverse with t as the starting point, and mark all accessible 1 (walls) of T with its shortest distance d1 in this process. For the second time, we start with F, and mark all accessible 1 of F with its shortest distance d2 in this process.

After that, let's enumerate the position of each 1. If it is marked by T and F at the same time, it means that t can reach f through this position, and this distance is the sum of their marked distances d1+d2. Then let's take a minimum value among all possibilities.