The theoretical content is recorded in the code Capriccio. Here I mainly write my own explanation and review, which is highly recommended

Code capriccio, code Capriccio PDF, code Capriccio Baidu online disk, code Capriccio knowledge planet, code Capriccio octet PDF, code Capriccio brush question route, code Capriccio knowledge planet octethttps://www.programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html

 

catalogue

Template 1: 2D array version

Template 2: one dimensional array Version (rolling array)

1: Split equal sum subset (01)

2: Weight of the last stone II (01 backpack)

3: Goals and (combinatorial problem)

4: one and zero

Full backpack:

5: Change 𞓜 (portfolio problem)

6: Change (sum)

Template 1: 2D array version

void test_2_wei_bag_problem1() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagweight = 4;

    // Two dimensional array
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));

    // initialization
    for (int j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    // The size of the weight array is the number of items
    for(int i = 1; i < weight.size(); i++) { // Traverse items
        for(int j = 0; j <= bagweight; j++) { // Traversal knapsack capacity
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

        }
    }

    cout << dp[weight.size() - 1][bagweight] << endl;
}

int main() {
    test_2_wei_bag_problem1();
}

Question:

(1) Initialization problem: you can't initialize to 0 or 1 by feeling at will. It should be based on the actual situation

When this point is the initial point, the data is brought in and checked, because this point is the cornerstone of all points

When this point is not the initial point, it is generally initialized to 0 (to prevent overwriting the data obtained later)

For example, in this template: initialize the first line to value[0]

The meaning is: when the backpack capacity > = 1, if only the first item is put, the maximum value of the backpack is value[0]

(2)for loop traversal sequence:

Generally, we first traverse the weight of items in positive order, and then the backpack capacity in positive order, but in fact, in a two-dimensional array, this order can be reversed, that is, traverse the backpack capacity in positive order, and then the weight of items in positive order;

Because they will not cover each other, they will not be affected, but the following one-dimensional array needs to be considered

(3) Recurrence formula problem: 01 knapsack template recurrence formula:

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

Meaning: dp[i][j] refers to the maximum value of taking any item with subscript [0-i] and putting it into the backpack with capacity of j

Returning means returning dp[weight.size()-1][bagweight], which is the last step of recursion

When no items are put in: there is no loss of backpack capacity, and the maximum value is equal to the value of the previous one (if you don't take it, the value remains the same)

When placing items: Backpack Capacity = Backpack Capacity - weight of items. The maximum value is equal to the value of the previous item + the value of new items

Template 2: one dimensional array Version (rolling array)

#include<vector>
#include <stack>
#include<queue>
#include<iostream>
using namespace std;
void test()
{
    vector<int> weight = { 1, 3, 4 };
    vector<int> value = { 15, 20, 30 };
    int bagweight = 4;
    //The core is: the weight of the goods as the bottom, the maximum capacity of the backpack as the ceiling, and the ceiling in turn until it is exactly equal to the bottom
    //Count the maximum value of dp[j] when the ceiling is lowered in turn
    //Then change the bottom again and repeat the above steps
    vector<int> dp(bagweight + 1, 0);
    for (int i = 0; i < weight.size(); i++)//Article weight
    {
        for (int j = bagweight; j >= weight[i]; j--)//Backpack Capacity
        {
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }

    cout << dp[bagweight] << endl;
}
int main()
{
	test();
	return 0;
}
dp[4]=max(dp[4]),dp[4-1]+15)=max(dp[4],dp[3]+15)  j=4
dp[3]=max(dp[3],dp[4-1]+15)=max(dp[3],dp[2]+15)  j=3
dp[2]=max(dp[2],dp[1]+15) j=2  ->>            
dp[1]=max(dp[1],dp[0]+15) j=1  ->>   dp[1]=max(0,15)=15

dp[4]=max(dp[4],dp[4-3]+vaule[1])=max(dp[4],dp[1]+20)=max(0,15+20)=35
dp[3]=max(dp[3],dp[3-3]+value[1])=max(dp[3],dp[0]+20)=max(0,0+20)=20

dp[4]=max(dp[4],dp[0]+value[2]=max(35,30)=35

Question:

(1) Traversal order problem:

This is different from the traversal order of the two-dimensional array. First, the weight of the items is traversed in the positive order, and then the capacity of the backpack is traversed in the reverse order. The reason is: in the reverse order, you will find that in the first traversal: my dp[4] will not affect dp[3]. Until the end of the first traversal, dp[1] will give us a specific value. In the second traversal, we are really recursive

Because it is difficult to understand, I write out the recursive process more sha easily (above)

Next, understand the meaning of "affected": suppose my second layer is positive order traversal

dp[1]=max(dp[1],dp[0]+15) j=1  ->>   dp[1]=max(0,15)=15
dp[2]=max(dp[2],dp[1]+15) j=2  ->>   dp[2]=max(0,30)=30
dp[3]=max(dp[3],dp[4-1]+15)=max(dp[3],dp[2]+15) dp[3]=45
dp[4]=max(dp[4]),dp[4-1]+15)=max(dp[4],dp[3]+15) dp[4]=60

You will find that item 1 is repeatedly put into the backpack, which is contrary to the condition that there is only one item specified in the title!

At the same time, the order of the two for loops cannot be reversed

(2) Initialization problem:

Initially, the array is initialized to 0. After one traversal, the array should not be modified to 15(value[0])

(3) recurrence formula:

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); (it's easy to understand: if it's bigger than you, it will be covered)

dp[j] at this time has the same meaning as dp[j] in dp[i][j] above: when the backpack capacity is j, the maximum value of backpack storage

1: Split equal sum subset (01)

Train of thought analysis:

The essence of this problem is to divide the array into two parts:

(1) Sum the array and record the sum as sum

·····1. If sum is an odd number, it proves that sum cannot be split into two parts. return false;

·····2 if sum is an even number, target=sum/2 is used

(2) Equivalent to just proving that the backpack with the capacity of target can be completed as long as its value is target when the capacity is full

The size of the number in the array is its weight and its value

The recurrence formula is: dp[j]=max(dp[j],dp[j-nums[i]]+nums[i])

(3) Judgment - > if it is equivalent to (2), it is expressed in Code: DP [target] = = target -- > return true;   else false;

class Solution {
public:
    bool canPartition(vector<int>& nums) {
    int sum = 0;
	vector<int>dp(10001, 0);
	for (int i = 0; i < nums.size(); i++) sum += nums[i];
	if (sum % 2) return false;
	int target = sum / 2;
	for (int i = 0; i < nums.size(); i++)
	{
		for (int j = target; j >= nums[i]; j--)
		{
			dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
		}
	}
	if (dp[target] == target) return true;
	return false;
    }
};

Q: why is the dp array 10001 so large?

Answer: because

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100
• The sum will not be greater than 20000. Only half of the backpack is required at most. For alignment, we need the subscript target

2: Weight of the last stone II (01 backpack)

Train of thought analysis:

This problem is easy to associate with dividing the array into two piles with the closest size, so as to obtain the optimal value

(1) Sum the array and record the sum as sum

Divide target=sum/2 into two parts, target and sum target

But note: when sum is even, the two stacks are equal

When sum is an odd number, target is smaller than sum target because target=sum/2, rounded down

(2) Since we are looking for the weight of the remaining stone, we just need to subtract the two. Of course, it's big - small

So we decided on the last step: return (sum DP [target]) - DP [target];

The next goal is to find dp[target]

(3) Recurrence formula

dp[j]=max(dp[j]，dp[j-nums[i]]+nums[i])

The value in the array is its size, which is also its value

class Solution {
public:
    int lastStoneWeightII(vector<int>& nums) {
    int sum = 0;
	vector<int> dp(15001, 0);
	for (int i = 0; i < nums.size(); i++) sum += nums[i];
	int target = sum / 2;
	for (int i = 0; i < nums.size(); i++)
	{
		for (int j = target; j >= nums[i]; j--)
		{
			dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
		}
	}
	return sum - dp[target] - dp[target];
    }
};

Explanation: I don't need to explain the size of dp too much^

3: Goals and (combinatorial problem)

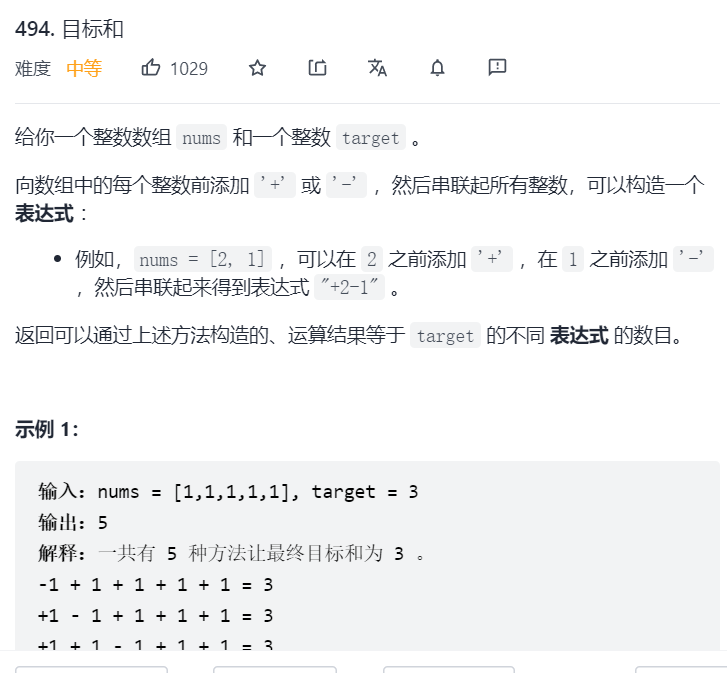
Train of thought analysis:

The difference between this question and the first two questions is that the first two questions seek value and the number of this question seeks truth

Since there is only addition and subtraction: let's assume that the number of additions is x and the total number is sum, then the number of subtractions is sum-x

That is: x-(sum-x)=target, target is the target value

We can discuss:

If the total sum < target: that is, the absolute value of all numbers is + or -, which is less than target, return 0;

Through the above formula, the expression of X is: x=(target+sum)/2;

Since x must be an integer, the values of target and sum must be even

This time is different from the previous knapsack problem. Before, we were looking for a knapsack with a capacity of j. how much can we hold at most.

There are several ways to solve this problem. In fact, this is a combinatorial problem

The recurrence formula is: dp[j] += dp[j - nums[i]]

dp[j] means: there are dp[j] methods to fill a bag with such a large volume as j (including j)

int findTargetSumWays(vector<int>& nums, int target) {
	int sum = 0;
	for (int i = 0; i < nums.size(); i++) sum += nums[i];
	if (abs(target) > sum) return 0;
	if ((sum + target) % 2 == 1) return 0;
	int bagsize = (sum + target) / 2;
	vector<int> dp(bagsize + 1, 0);
	dp[0] = 1;
	for (int i = 0; i < nums.size(); i++)
	{
		for (int j = bagsize; j >= nums[i]; j--)
		{
			dp[j] += dp[j - nums[i]];
		}
	}
	return dp[bagsize];
}

Explanation: about the initialization of dp: dp[0]=1. When the capacity is 0, there is only one way to fill it: do not fill it

Although this explanation is far fetched, we can see from the recursive formula that if the initialization is 0, all results are 0

4: one and zero

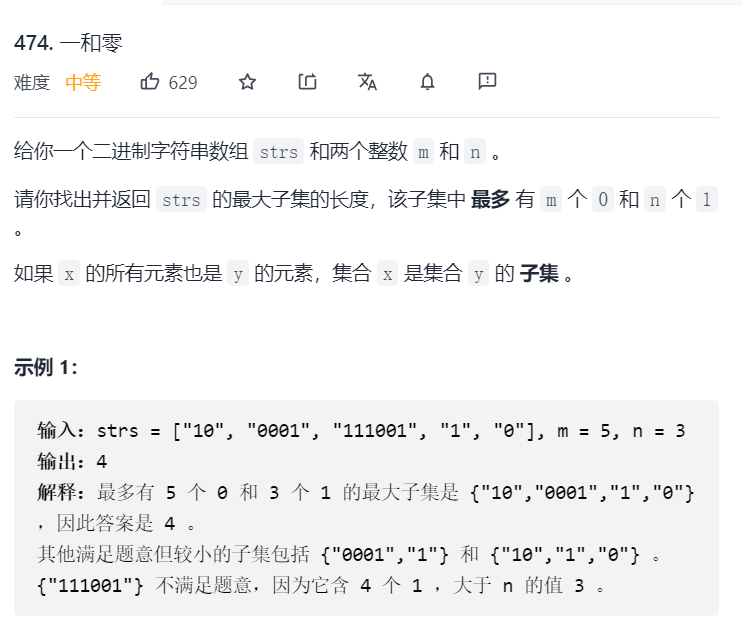
Train of thought analysis:

Let you return the longest string that meets this condition

This problem is difficult... Because its weight becomes two kinds, the quantity of 0 and the quantity of 1. What's the value? Number of strings

It can be simply understood as: weight is consumed, and value is the result we want

(1) Traverse the whole large string, traverse the small string in the large string, traverse the small string with characters, and count the number of 0 and 1

(2) Traversal order: the outermost layer is a large string (the weight of the item), and the inner layer is (the capacity of the backpack) (there are two inner layers!)

(3) Recurrence formula: because this is to find the best (not the number of methods of 3 questions), it is not a combinatorial problem

dp[i][j]=max(dp[i][j]，dp[i-zerosize][j-onesize]+1);

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // Default initialization 0
        for (string str : strs) { // Traverse items
            int oneNum = 0, zeroNum = 0;
            for (char c : str) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int i = m; i >= zeroNum; i--) { // Traverse the backpack capacity and traverse from back to front!
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
};

Full backpack:

(1) Different times

Different from 01 knapsack, the same item can only be taken once in 01 knapsack problem, while it can be taken countless times in complete knapsack problem (as long as the knapsack capacity is enough)

(2) Different times lead to different traversal order

In the 01 knapsack, the for loop of the second layer traverses the capacity of the knapsack in reverse order

In a complete knapsack, with the for loop of the second layer, we can traverse the capacity of the knapsack in positive order

(3) combinatorial problem and sequencing problem

Traversal mode of combinatorial problem: first items and then knapsack (all in positive order)

Traversal method of permutation problem: change backpack and then items (all in positive order)

Full backpack template:

// First traverse the items, then traverse the backpack
void test_CompletePack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // Traverse items
        for(int j = weight[i]; j <= bagWeight; j++) { // Traversal knapsack capacity
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}
int main() {
    test_CompletePack();
}

5: Change 𞓜 (portfolio problem)

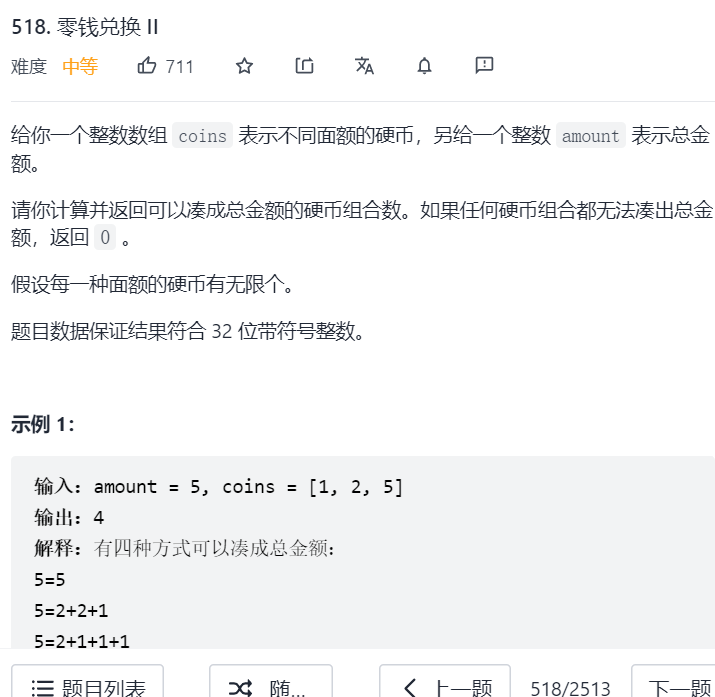
Train of thought analysis:

Calculate the total number of combinations without considering the order

Because it is the total number of combinations, the traversal order is: items first and then backpacks

Because it is the total number of combinations, the recurrence formula is: dp[j]=dp[j-nums[i]]

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount + 1, 0);
        dp[0] = 1;
        for (int i = 0; i < coins.size(); i++) { // Traverse items
            for (int j = coins[i]; j <= amount; j++) { // Traversal knapsack
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
};

6: Change (sum)

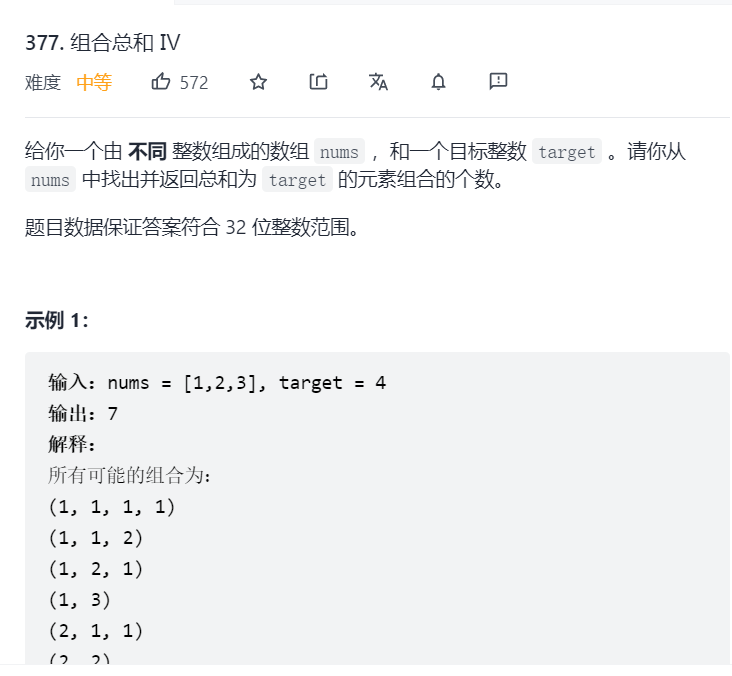
Train of thought analysis:

This question is the proper total number of permutations

Because it is the total number of permutations, the traversal order is: backpack first and then items

Because it is the total number of permutations, the recurrence formula is: dp[i] + = dp[i - nums[j]]; (exactly the same)

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
    vector<unsigned int> dp(target + 1, 0);
        dp[0] = 1;
        for (int i = 0; i <= target; i++) { // Traversal knapsack
            for (int j = 0; j < nums.size(); j++) { // Traverse items
                if (i - nums[j] >= 0 ) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
};

Explanation: to prevent overflow, I changed the type of dp to unsigned int. during this period, I tried int, long and long will overflow

I simply changed it to unsigned int. unexpectedly, it passed ^^

The question data ensures that the answer conforms to the 32-bit integer range

When I ask the boss clearly, I'll add ^^