A. Team up
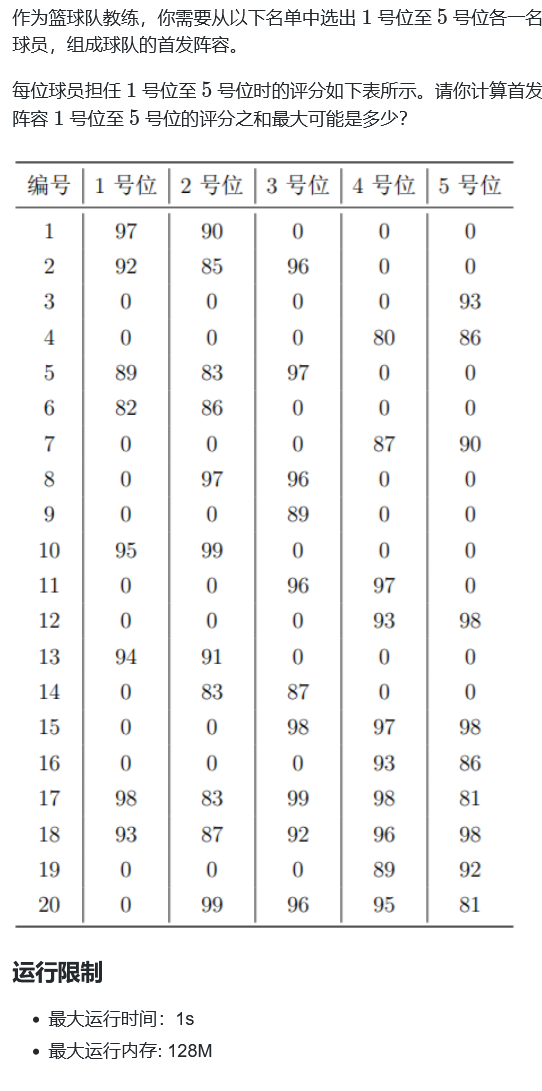
Answer: 490
This question is very simple. You can calculate it directly by hand, find the highest score in each column, and do not repeat it. If there is repetition, you can choose the next highest score
B year string
[problem description]
Xiao Ming uses the letter A to correspond to the number 1, B to correspond to 2, and so on, and Z to correspond to 26. For numbers above 27, Xiaoming corresponds with a string of two or more bits, for example, AA corresponds to 27, AB corresponds to 28, AZ corresponds to 52, and LQ corresponds to 329.
What is the string corresponding to 2019?
#include <iostream>
using namespace std;
char s[27] = {0,'A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z'};
int main(){
int n;
string ans;
cin >> n;
while(n){
ans += s[n % 26];
n /= 26;
}
int len = ans.length();
for(int i=len-1; i>=0; i--)
cout << ans[i];
return 0;
}
Answer: BYQ
26 base
C: Sequence evaluation
[problem description]
Given the sequence 1, 1, 1, 3, 5, 9, 17,..., starting from item 4, each item is the sum of the first three items. Find the last four digits of item 20190324.
#include <iostream>
using namespace std;
const int mod = 1e4;
long long f[20190330];
int main(){
f[1] = f[2] = f[3] = 1;
for(int i=4; i<=20190324; i++){
f[i] = (f[i-1] + f[i-2] + f[i-3]) % mod;
}
cout << f[20190324] << endl;;
return 0;
}
Answer: 4659
Like Fibonacci, you need to take the remainder every step
D: Decomposition of number
[problem description]
2019 is decomposed into the sum of three different positive integers, and each positive integer is required to contain no numbers 2 and 4. How many different decomposition methods are there? Note that the order of exchanging three integers is regarded as the same method. For example, 1000 + 1001 + 18 and 1001 + 1000 + 18 are regarded as the same method.
#include<iostream>
using namespace std;
int flag(int x){
if(x<=0) return 0;
while(x){
int ans=x%10;
if(ans==2 || ans==4) return 0;
x/=10;
}
return 1;
}
int main(){
int n=2019,ans=0;
for(int i=1;i<2019;i++){
if(flag(i)){
for(int j=i+1;j<2019;j++){
if(flag(j)){
int k=2019-i-j;
if(flag(k) && k>j)
ans++;
}
}
}
}
cout << ans;
return 0;
}
Answer: 40785
Direct violence
E: Labyrinth
[problem description]
The following figure shows the plan of a maze, where the one marked with 1 is an obstacle and the one marked with 0 is an accessible place.
010000 000100 001001 110000
The entrance of the maze is the upper left corner and the exit is the lower right corner. In the maze, you can only walk from one position to one of its upper, lower, left and right directions. For the above maze, starting from the entrance, you can pass through the maze in the order of DRRURRDDDR, with a total of 10 steps. Where D, u, L and R respectively represent going down, up, left and right. For the following more complex maze (30 rows and 50 columns), please find a way to pass through the maze, which uses the least number of steps. On the premise of the least number of steps, please find the one with the smallest dictionary order as the answer. Please note that in the dictionary order, d < L < R < U. (if you copy the following text into a text file, be sure to check whether the copied content is consistent with that in the document. There is a file maze.txt in the test question directory, and the content is the same as the following text)
01010101001011001001010110010110100100001000101010 00001000100000101010010000100000001001100110100101 01111011010010001000001101001011100011000000010000 01000000001010100011010000101000001010101011001011 00011111000000101000010010100010100000101100000000 11001000110101000010101100011010011010101011110111 00011011010101001001001010000001000101001110000000 10100000101000100110101010111110011000010000111010 00111000001010100001100010000001000101001100001001 11000110100001110010001001010101010101010001101000 00010000100100000101001010101110100010101010000101 11100100101001001000010000010101010100100100010100 00000010000000101011001111010001100000101010100011 10101010011100001000011000010110011110110100001000 10101010100001101010100101000010100000111011101001 10000000101100010000101100101101001011100000000100 10101001000000010100100001000100000100011110101001 00101001010101101001010100011010101101110000110101 11001010000100001100000010100101000001000111000010 00001000110000110101101000000100101001001000011101 10100101000101000000001110110010110101101010100001 00101000010000110101010000100010001001000100010101 10100001000110010001000010101001010101011111010010 00000100101000000110010100101001000001000000000010 11010000001001110111001001000011101001011011101000 00000110100010001000100000001000011101000000110011 10101000101000100010001111100010101001010000001000 10000010100101001010110000000100101010001011101000 00111100001000010000000110111000000001000000001011 10000001100111010111010001000110111010101101111000
#include<iostream>
#include<queue>
using namespace std;
int dir[4][2]={1,0,0,-1,0,1,-1,0};
string point="DLRU";
char ans[1001];
string maze[35];
int n=30,m=50;
int vis[30][50]={0};
typedef pair<int,int> p;
typedef pair<p,string> P;
queue<P> que;
int main(){
for(int i=0;i<n;i++){
cin >> maze[i];
}
que.push(P(p(0,0),""));
vis[0][0]=1;
while(!que.empty()){
P now = que.front();
que.pop();
p res=now.first;
if(res.first==n-1 && res.second==m-1){
cout << now.second;
return 0;
}
for(int i=0;i<4;i++){
int x=res.first+dir[i][0];
int y=res.second+dir[i][1];
if((x>=0&&x<n&&y>=0&&y<m)&&vis[x][y]==0&&maze[x][y]=='0'){
vis[x][y]=1;
que.push(P(p(x,y),now.second+point[i]));
}
}
}
return 0;
}
DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR
Direct BFS
F: Sum of special numbers
Time limit: 1.0s memory limit: 256.0MB total score of this question: 15 points
[problem description]
Xiao Ming is very interested in numbers containing 2, 0, 1 and 9 (excluding the leading 0). In the range of 1 to 40, such numbers include 1, 2, 9, 10 to 32, 39 and 40, a total of 28, and their sum is 574. What is the sum of all such numbers in 1 to n?
[input format]
The input line contains two integers n.
[output format]
Output a line containing an integer representing the sum of the numbers that meet the conditions.
[sample input] 40
[sample output] 574
#include <iostream>
using namespace std;
int n;
long long sum;
int main(){
cin >> n;
for(int i=1; i<=n; i++){
int t = i;
while(t){
if(t%10 == 2 || t%10 == 0 || t%10 == 1 || t%10 == 9) {
sum += i;
break;
}
t /= 10;
}
}
cout << sum;
return 0;
}
G: Weight of complete binary tree
Time limit: 1.0s memory limit: 256.0MB total score of this question: 20 points
[problem description] given a complete binary tree with N nodes, each node in the tree has a weight, which is A1, A2 and ··· AN from top to bottom and from left to right, as shown in the following figure:
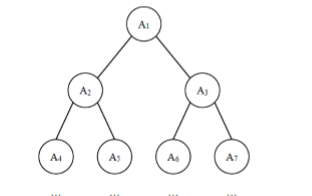
Now Xiao Ming wants to add up the weights of nodes with the same depth. He wants to know which depth has the largest sum of node weights? If the weight sum of multiple depths is the largest, please output the smallest depth. Note: the depth of the root is 1.
[input format]
The first line contains an integer N.
The second line contains N integers A1, A2, ··· AN.
[output format]
Output an integer representing the answer.
[sample input]
7
1 6 5 4 3 2 1
[sample output]
2
#include<iostream>
#include<cmath>
using namespace std;
int main(){
int n,sum=0,deep=0,maxx=-1000000,minn=0;
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x;
scanf("%d",&x);
sum+=x;
if(i==pow(2,deep) || i==n){
if(maxx<sum){
maxx=sum;
minn=deep;
}
deep++;
sum=0;
}
}
printf("%d",minn);
return 0;
}
H: Arithmetic sequence
Time limit: 1.0s memory limit: 256.0MB total score of this question: 20 points
[problem description]
The math teacher gave Xiao Ming a problem of summing the arithmetic sequence. But the careless Xiao Ming forgot part of the sequence and only remembered N integers. Now give these N integers. Xiao Ming wants to know how many items are the shortest arithmetic sequence containing these N integers?
[input format]
The first line of input contains AN integer N. The second line contains N integers A1,A2, ····, AN. (note that A1 ∼ AN is not necessarily given in the order of the arithmetic sequence)
[output format]
Output an integer to represent the answer.
[sample input]
5 2 6 4 10 20
[sample output]
10
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
int main()
{
int n,a[100005],ind;
cin >> n;
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
ind=a[1]-a[0];
if(ind==0) return !(cout<<n<<endl);
sort(a,a+n);
for(int i=1;i<n;i++){
ind=__gcd(ind,a[i]-a[i-1]);
}
cout << (a[n-1]-a[0])/ind+1 << endl;
return 0;
}
1: Suffix expression
Time limit: 1.0s memory limit: 256.0MB total score of this question: 25 points
[problem description]
Given n plus signs, M minus signs and N + M + 1 integers A1, A2, ···, AN+M+1, Xiao Ming wants to know which of all the legal suffix expressions rounded up by N plus signs, M minus signs and N + M + 1 integers has the largest result?
Please output this maximum result.
For example, if 1 2 3 + -, the result of the suffix expression "2 3 + 1 -" is 4, which is the largest.
[input format]
The first line contains two integers N and M.
The second line contains N + M + 1 integers A1, A2, ···, AN+M+1.
[output format]
Output an integer representing the answer.
[sample input]
1 1
1 2 3
[sample output]
4
#include <iostream>
#include <algorithm>
using namespace std;
int n, m, t, res = 0;
int a[200010];
int main()
{
cin >> n >> m;
t = n+m+1;
for(int i=0; i<t; i++)
cin >> a[i];
sort(a, a+t, greater<int>());
for(int i=0; i<n+1; i++)
res += a[i];
for(int i=n+1; i<t; i++)
res -= a[i];
cout << res << endl;
return 0;
}
J: Psionic transmission
Time limit: 1.0s memory limit: 256.0MB total score of this question: 25 points
[title background]
In the game "StarCraft II", the high-level Templar, as an important AOE unit of the star spirit, plays an important role in the middle and later stages of the game. Its skill "psionic storm" can consume a lot of psionics and cause destructive damage to the enemy in an area. It is often used against low health units such as human biochemical forces and Zerg Hydra flying dragons.
[problem description]
You control n high-ranking Templars, marked 1, 2,..., n for convenience. Each high-level Templar needs a certain amount of psionics to fight. Each person has a psionic value AI, which indicates how much psionics he has (non negative AI means that the high-level Templar has AI more psionics than in the best state, and negative AI means that the high-level Templar needs − AI more psionics to reach the best combat state). Now the system gives your high-level Templar an ability to transmit psionics. Each time you can choose an i ∈ [2, n − 1]. If AI ≥ 0, the high-level Templar on both sides, that is, i − 1 and i + 1, will draw AI psionics from i, the high-level Templar; If AI < 0, the two high-level Templars on both sides, i − 1 and i + 1, will give the high-level Templar i − AI some power. Formally speaking, AI − 1 += ai, ai+1 += ai, ai − = 2ai.
Psionics are very efficient combat tools, but also very dangerous and unstable. It is not good for a high-level Templar to have too much or too little psionics. Define the instability of a group of high-level Templar as maxni=1|ai|. Please transfer psionics for an unlimited number of times to minimize the instability of the group of high-level Templar you control.
[input format]
This question contains several groups of questions. The first line of input contains a positive integer T, which indicates the number of query groups.
Next, enter each set of queries in turn.
The first line of each query contains a positive integer n, indicating the number of high-level Templars.
The next line contains n numbers a1, a2,..., an.
[output format]
Output T line. An integer in each line represents the answers of each group of questions in turn.
[sample input]
3
3
5 -2 3
4
0 0 0 0
3
1 2 3
[sample output]
3
0
3
The answer to this question comes from https://blog.csdn.net/belous_zxy/article/details/88901019
#include <algorithm>
#include <cstring>
#include <iostream>
#include <limits.h>
using namespace std;
typedef long long LL;
const int N = 300010;
int n;
LL sum[N], a[N], s0, sn;
bool st[N];
int main()
{
int T;
scanf("%d", &T);
while (T--)
{
scanf("%d", &n);
sum[0] = 0;
for (int i = 1; i <= n; i++)
{
scanf("%lld", &sum[i]);
sum[i] += sum[i - 1];
}
s0 = sum[0], sn = sum[n];
if (s0 > sn)
swap(s0, sn);
sort(sum, sum + n + 1);
for (int i = 0; i <= n; i++)
if (s0 == sum[i])
{
s0 = i;
break;
}
for (int i = n; i >= 0; i--)
if (sn == sum[i])
{
sn = i;
break;
}
memset(st, 0, sizeof st);
int l = 0, r = n;
for (int i = s0; i >= 0; i -= 2)
{
a[l++] = sum[i];
st[i] = true;
}
for (int i = sn; i <= n; i += 2)
{
a[r--] = sum[i];
st[i] = true;
}
for (int i = 0; i <= n; i++)
if (!st[i])
{
a[l++] = sum[i];
}
LL res = 0;
for (int i = 1; i <= n; i++)
res = max(res, abs(a[i] - a[i - 1]));
printf("%d\n", res);
}
return 0;
}