Attach the title link, ideas and code. Please eat by yourself
Xiao Zheng's doubts and harmonic series / number theory thinking
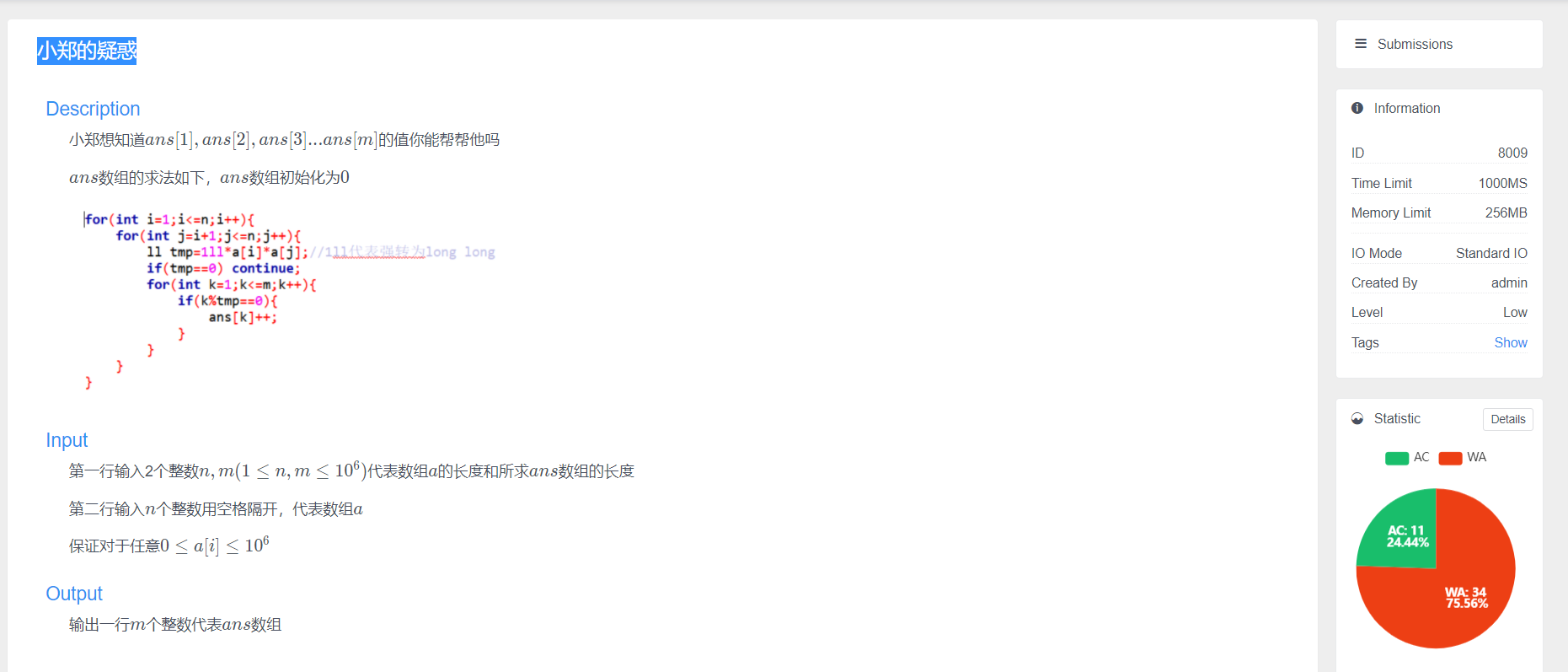
Meaning:
Give N numbers
If I = [1,M] is divisible, ans[i] + + outputs the final ans array.
Train of thought analysis:
First, count the number of K, and use unmap to query faster. We enumerate i=1 – m, then enumerate their multiple k*i, and then solve another factor. If the factor is just equal to K, then for the number k, the number of contributions that can be modulo is the combination number of C (number of factors, 2). If the two factors are not equal, the multiplication principle is directly used. After preprocessing, enumerate as above again
Period record ans[k * i] + = contribution [i]
ll ans[1000010];
ll op[1000010];
ll vis[1000010];
signed main()
{
ll n;
read(n);
ll m;
read(m);
ll cnt=0;
for(int i=1; i<=n; i++)
{
ll x;
read(x);
vis[x]++;
}
for(int i=1; i<=m; i++)
{
if(!vis[i])
continue;
for(int j=i; j<=m; j=j+i)
{
ll now=j/i;
if(now==i)
{
ans[j]+=(vis[i]*(vis[i]-1))/2;
continue;
}
if(now>i)
{
ans[j]+=vis[now]*vis[i];
}
}
}
for(int i=1; i<=m; i++)
{
for(int j=i; j<=m; j=j+i)
{
op[j]+=ans[i];
}
}
for(int i=1; i<=m; i++)
{
printf("%lld ",op[i]);
}
}
operation interval dp topic link
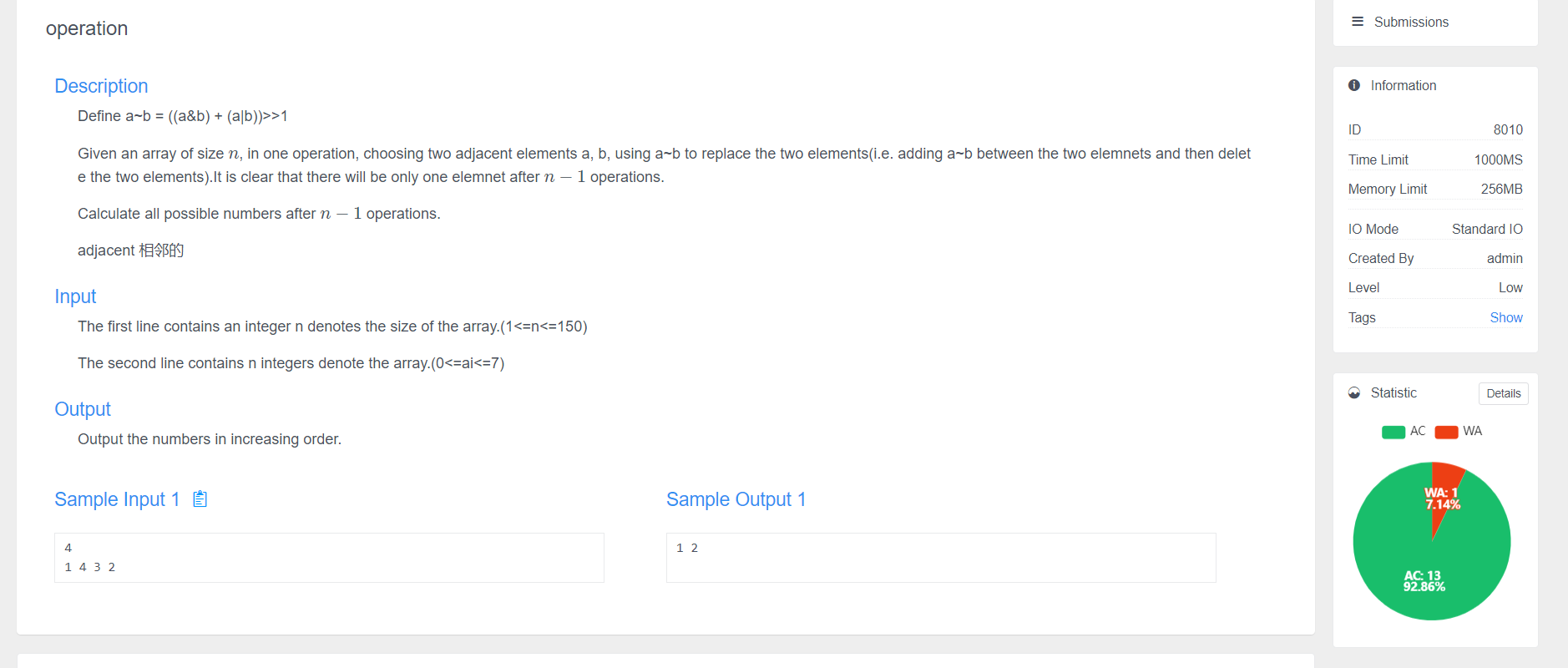
Main idea of the title:
N numbers, define operation: take two adjacent numbers a and B, then remove a and B, merge them into (a+b)/2, and put them in the original position until there is only one number left in the sequence. The number that may be left in the end is output in ascending order.
Problem solving ideas:
Considering the interval dp, define dp[i][j][k] =0/1, which means that when the interval [i,j] can form K, it is 1, otherwise it is 0
Then you just need to transfer by interval.
ll dp[160][160][8];
ll a[200];
signed main()
{
ll n;
read(n);
for(int i=1; i<=n; i++)
{
read(a[i]);
dp[i][i][a[i]]=1;
}
for(int len=1; len<=n; len++)
{
for(int i=1; i<=n; i++)
{
int j=i+len;
if(j>n)
break;
for(int k=0; k<j; k++)
{
for(int p=0; p<=7; p++)
{
for(int q=0; q<=7; q++)
{
if(dp[i][k][p]&&dp[k+1][j][q])
dp[i][j][(p+q)/2]=1;
}
}
}
}
}
for(int i=0; i<=7; i++)
{
if(dp[1][n][i])
{
printf("%lld ",i);
}
}
}
Wall climbing trip status compression dp (tick bar)
Can't do it. Attach a big man's blog
atcoder 213 G problem solution
Find Subsequence segment tree maintenance exclusion

Meaning:
Output the number of subsequences in a sequence of length N that meet the requirement of "subsequences appear only once in the whole sequence"
Problem solving ideas:
Define dp[i] as the total number of legal sequences ending with ai. If the current ai does not appear for the first time, it is necessary to exclude the location where the previous ai appears.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
const int mod=998244353;
int a[N],last[N];
ll f[N],s[N];//At the i th number, the number of schemes that appear only once
int vis[N];
struct SegTree{
int l,r;
ll sum;
}Tr[N<<2];
void pushup(int u)
{
Tr[u].sum=(Tr[u<<1].sum+Tr[u<<1|1].sum)%mod;
}
void build(int u,int L,int R)
{
Tr[u].l=L,Tr[u].r=R;
if(L==R) return;
int mid=(L+R)>>1;
build(u<<1,L,mid);
build(u<<1|1,mid+1,R);
}
void add(int u,int L,int R,ll val)
{
if(Tr[u].l>R||Tr[u].r<L) return;
if(Tr[u].l>=L&&Tr[u].r<=R)
{
Tr[u].sum=((Tr[u].sum+val)%mod+mod)%mod;
f[L]=((f[L]+val)%mod+mod)%mod;
return;
}
add(u<<1,L,R,val);
add(u<<1|1,L,R,val);
pushup(u);
}
ll query(int u,int L,int R)
{
if(Tr[u].l>R||Tr[u].r<L) return 0;
if(Tr[u].l>=L&&Tr[u].r<=R) return Tr[u].sum;
return (query(u<<1,L,R)+query(u<<1|1,L,R))%mod;
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1; i<=n; i++)
scanf("%d",&a[i]);
build(1,1,n);
for(int i=1; i<=n; i++)
{
ll res;
if(last[a[i]])
res=query(1,1,i-1)-query(1,1,last[a[i]]-1);
// (1----i-1)
// First occurrence DP [i]= Σ (dp[i-1]) +1
else
res=query(1,1,i-1)+1;
res%=mod;
res+=mod;
res%=mod;
//cout<<res<<endl;
add(1,i,i,res);
if(last[a[i]])
add(1,last[a[i]],last[a[i]],-f[last[a[i]]]);
last[a[i]]=i;
}
printf("%lld\n",query(1,1,n));
return 0;
}
Recursion on the check-in dictionary tree
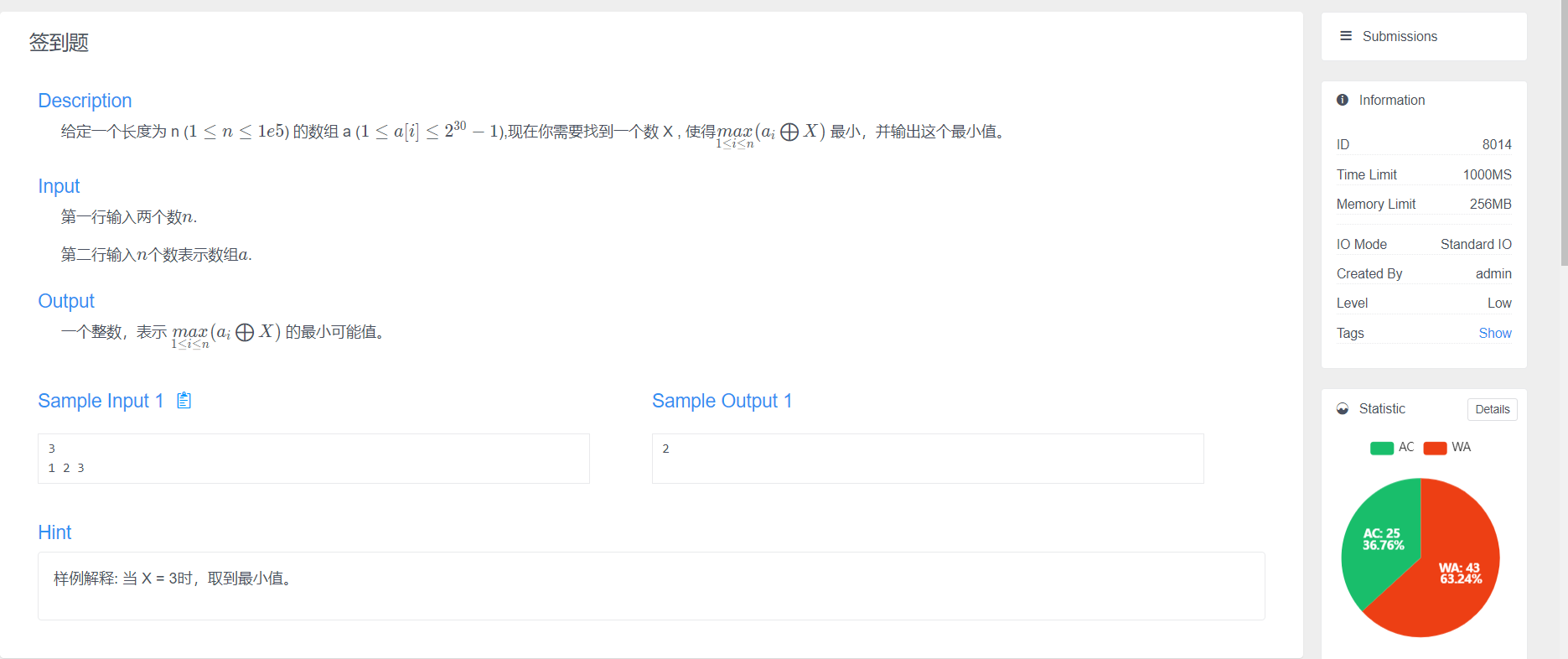
Problem solving ideas
Firstly, the dictionary tree of ai is established, and the high order is inserted in front.
Then start calculating the answer. First, if the current position has 0 and 1, it means that whether the X bit is 0 or 1 at this time, it cannot affect the existence of 1 on the XOR result bit. Therefore, we need to recurse to the left and right sons of the dictionary tree.
If there is only 0 or 1, the XOR result must not contain the binary of this bit, which is directly recursive in one direction.
#include<stdlib.h>
#include<algorithm>
#include<string.h>
#include<stdio.h>
#include <iostream>
#include<time.h>
#include <string>
#define ll long long
#define inf 0x3f3f3f3f
#define mods 1000000007
#define modd 998244353
#define PI acos(-1)
#define fi first
#define se second
#define lowbit(x) (x&(-x))
#define mp make_pair
#define pb push_back
#define si size()
#define E exp(1.0)
#define fixed cout.setf(ios::fixed)
#define fixeds(x) setprecision(x)
#define IOS ios::sync_with_stdio(false);cin.tie(0)
using namespace std;
ll gcd(ll a,ll b){if(a<0)a=-a;if(b<0)b=-b;return b==0?a:gcd(b,a%b);}
template<typename T>void read(T &res){bool flag=false;char ch;while(!isdigit(ch=getchar()))(ch=='-')&&(flag=true);
for(res=ch-48;isdigit(ch=getchar());res=(res<<1)+(res<<3)+ch - 48);flag&&(res=-res);}
ll lcm(ll a,ll b){return a*b/gcd(a,b);}
ll qp(ll a,ll b,ll mod){ll ans=1;if(b==0){return ans%mod;}while(b){if(b%2==1){b--;ans=ans*a%mod;}a=a*a%mod;b=b/2;}return ans%mod;}//Fast power%
ll qpn(ll a,ll b, ll p){ll ans = 1;a%=p;while(b){if(b&1){ans = (ans*a)%p;--b;}a =(a*a)%p;b >>= 1;}return ans%p;}//Inverse element (numerator * QP (denominator, mod-2,mod))%mod;
const int maxn=32*1e5+520;
ll nex[maxn][2], cnt=1;
ll exist[maxn];
ll rnmb=1e18;
struct trie
{
void insert(ll num)
{
ll p =0;
for (int i = 32; i >=0; i--)
{
int c = ((num>>i)&1);
if (!nex[p][c])
{
exist[cnt]=0;
memset(nex[cnt],0,sizeof(nex[cnt]));
nex[p][c] = cnt++;
} // If not, add a node
p = nex[p][c];
}
exist[p]=num;
}
void find(ll now,ll p,ll cur)
{
if (nex[p][0]&&nex[p][1])
{
cur=cur+(1<<now);
if(now==0){
rnmb=min(rnmb,cur);
return ;
}
find(now-1,nex[p][0],cur);
find(now-1,nex[p][1],cur);
return ;
}
if (!nex[p][0])
{
if(now==0){
rnmb=min(rnmb,cur);
return ;
}
find(now-1,nex[p][1],cur);
return ;
}
if (!nex[p][1])
{
if(now==0){
rnmb=min(rnmb,cur);
return ;
}
find(now-1,nex[p][0],cur);
return ;
}
}
} tree;
int main()
{
ll t;
t=1;
ll ak=0;
while(t--)
{
ll n,m;
cnt=1;
ak++;
memset(nex,0,sizeof(nex));
memset(exist,0,sizeof(exist));
read(n);
m=1;
for(int i=1; i<=n; i++)
{
ll x;
read(x);
tree.insert(x);
}
tree.find(32,0,0);
printf("%lld",rnmb);
}
return 0;
}
Number Game title link
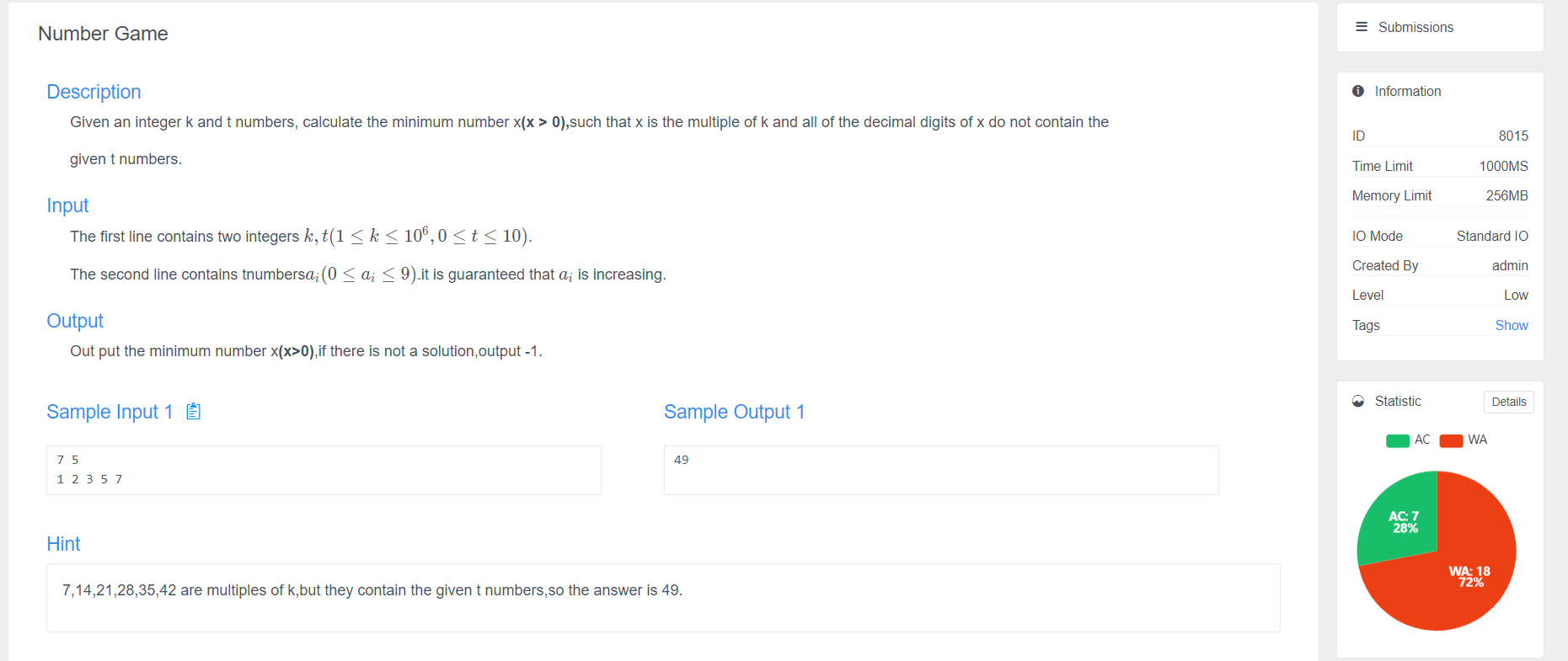
bfs is considered in solving the minimum value. According to the congruence theorem, if the result Q after module appears twice in the search process, it shows that it is futile to continue the search, and you can prune here directly. Otherwise, search and record the path for backtracking.
ll a[30];
queue<pair<ll,ll> >q;
ll mo[1000009];
ll lastf[1000009];
ll lasts[1000009];
vector<ll>ans;
signed main()
{
ll k;
read(k);
ll n;
read(n);
for(int i=1; i<=n; i++)
{
ll x;
read(x);
a[x]=1;
}
ll now=1;
q.push(mp(now,0));
while(q.size())
{
ll ve=q.front().se;
ll pre=q.front().fi;
q.pop();
for(int i=0; i<=9; i++)
{
if(a[i])
continue;
ll op=(ve*10+i)%k;
if(mo[op])
continue;
if(op==0)
{
if(i==0&&now==1)
continue;
ans.push_back(i);
while(pre>1)
{
ans.push_back(lasts[pre]);
pre=lastf[pre];
}
for(int j=ans.size()-1; j>=0; j--)
{
printf("%lld",ans[j]);
}
return 0;
}
mo[op]=1;
lastf[++now]=pre;
lasts[now]=i;
q.push(mp(now,op));
}
}
printf("-1");
}
Link to one question
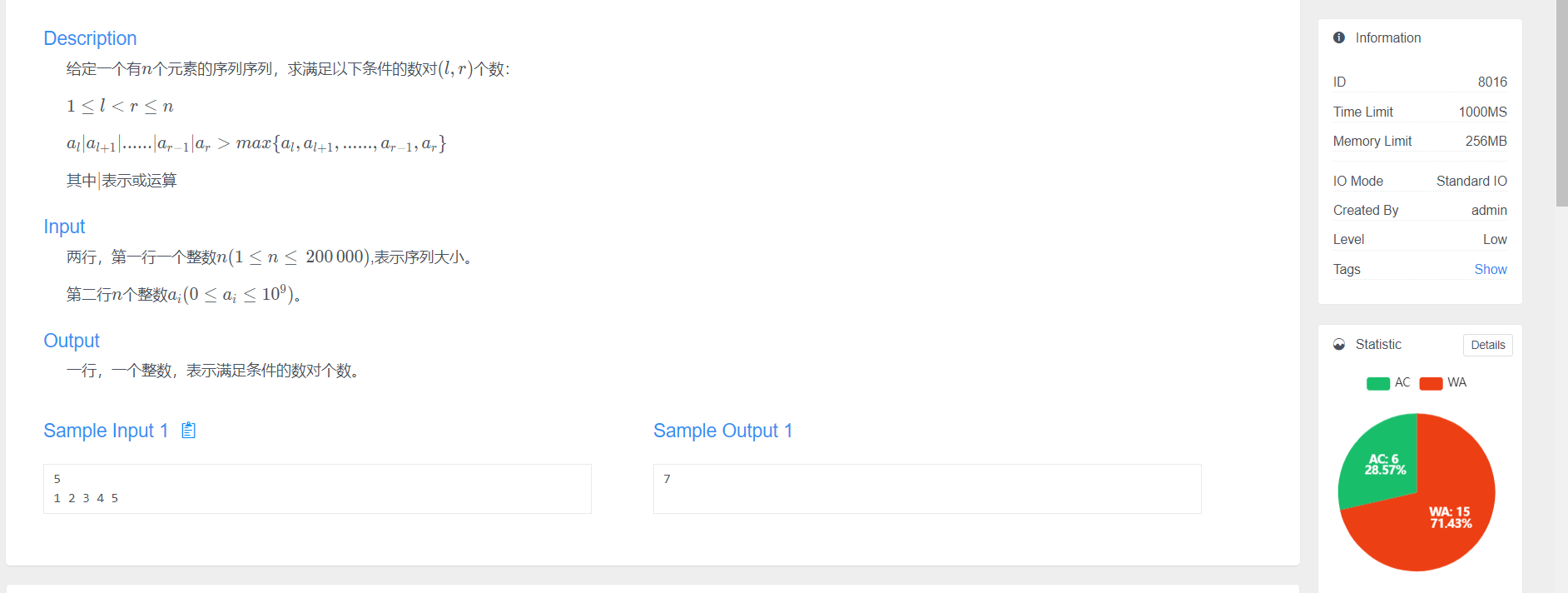
First, if the interval is greater than the maximum value of the interval, it means that there must be a number that is not the maximum value in the interval, and there is a binary bit on the number, which can be passed or supplemented to the bit of the maximum value. Then we can enumerate each ai and determine the interval endpoint with ai as the maximum value by the method of segment tree dichotomy. This step also requires a preprocessing. The N numbers are binary disassembled in a row, and then the binary bits without ai are left and right. The nearest legal position can be found in the interval, and then the contribution can be calculated happily.
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <deque>
#include <cmath>
#include <ctime>
#include <map>
#include <set>
#include <unordered_map>
#include <bitset>
#define fi first
#define se second
#define pb push_back
// #define endl "\n"
#define debug(x) cout << #x << ":" << x << endl;
#define bug cout << "********" << endl;
#define all(x) x.begin(), x.end()
#define lowbit(x) x & -x
#define fin(x) freopen(x, "r", stdin)
#define fout(x) freopen(x, "w", stdout)
#define ull unsigned long long
#define ll long long
const double eps = 1e-5;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const double pi = acos(-1.0);
const int mod = 1e9 + 7;
const int maxn = 2e5 + 10;
using namespace std;
#define lson rt << 1
#define rson rt << 1 | 1
unordered_map<int, int> mp;
struct node{
int maxx;
int p;
}t[maxn << 2];
int s[maxn], ans, n;
void pushup(int rt){
t[rt].maxx = max(t[lson].maxx, t[rson].maxx);
t[rt].p = t[lson].p | t[rson].p;
}
void build(int rt, int l, int r){
if(l == r){
t[rt].maxx = t[rt].p = s[l];
return ;
}
int mid = l + r >> 1;
build(lson, l, mid), build(rson, mid + 1, r);
pushup(rt);
}
int querymaxxl(int rt, int l, int r, int pos) {
if(l >= pos)return 1;
if(l == r) {
if(t[rt].maxx > s[pos])return l;
else return 1;
}
int mid = l + r >> 1, ret = 1;
if(r < pos) {
if(t[rson].maxx > s[pos]){
ret = max(ret, querymaxxl(rson, mid + 1, r, pos));
}
else if(t[lson].maxx > s[pos]){
ret = max(ret, querymaxxl(lson, l, mid, pos));
}
}
else if(l <= pos && pos <= r){
if(t[rson].maxx > s[pos])ret = max(ret, querymaxxl(rson, mid + 1, r, pos));
if(t[lson].maxx > s[pos])ret = max(ret, querymaxxl(lson, l, mid, pos));
}
return ret;
}
int querymaxxr(int rt, int l, int r, int pos){
if(r <= pos)return n;
if(l == r){
if(t[rt].maxx > s[pos])return l;
else return n;
}
int mid = l + r >> 1, ret = n;
if(pos < l){
if(t[lson].maxx > s[pos]){
ret = min(ret, querymaxxr(lson, l, mid, pos));
}
else if(t[rson].maxx > s[pos]){
ret = min(ret, querymaxxr(rson, mid + 1, r, pos));
}
}
else if(l <= pos && pos <= r){
if(t[lson].maxx > s[pos])ret = min(ret, querymaxxr(lson, l, mid, pos));
if(t[rson].maxx > s[pos])ret = min(ret, querymaxxr(rson, mid + 1, r, pos));
}
return ret;
}
bool check(int &a, int &b){
if((a | b) > a)return true;
else return false;
}
int queryhl(int rt, int l, int r, int pos){
if(l >= pos)return -1;
if(l == r) {
if(check(ans, t[rt].p))return l;
else return -1;
}
int mid = l + r >> 1, ret = -1;
if(r < pos) {
if(check(ans, t[rson].p)){
ret = max(ret, queryhl(rson, mid + 1, r, pos));
}
else if(check(ans, t[lson].p)){
ret = max(ret, queryhl(lson, l, mid, pos));
}
}
else if(l <= pos && pos <= r){
if(check(ans, t[rson].p))ret = max(ret, queryhl(rson, mid + 1, r, pos));
if(check(ans, t[lson].p))ret = max(ret, queryhl(lson, l, mid, pos));
}
return ret;
}
int queryhr(int rt, int l, int r, int pos){
if(r <= pos)return inf;
if(l == r){
if(check(ans, t[rt].p))return l;
else return inf;
}
int mid = l + r >> 1, ret = inf;
if(pos < l){
if(check(ans, t[lson].p)){
ret = min(ret, queryhr(lson, l, mid, pos));
}
else if(check(ans, t[rson].p)){
ret = min(ret, queryhr(rson, mid + 1, r, pos));
}
}
else if(l <= pos && pos <= r){
if(check(ans, t[lson].p))ret = min(ret, queryhr(lson, l, mid, pos));
if(check(ans, t[rson].p))ret = min(ret, queryhr(rson, mid + 1, r, pos));
}
return ret;
}
int main(){
// freopen("in.txt", "r", stdin);
scanf("%d", &n);
for(int i = 1; i <= n; i ++)scanf("%d", &s[i]);
build(1, 1, n);
ll sum = 0;
for(int i = 1; i <= n; i ++){
int pos1, pos11, pos22, pos2;
ans = s[i];
pos1 = querymaxxl(1, 1, n, i);
if(i != pos1 && s[pos1] > s[i])pos1 ++;
pos1 = max(mp[s[i]], pos1);
pos2 = querymaxxr(1, 1, n, i);
if(i != pos2 && s[pos2] > s[i])pos2 --;
mp[s[i]] = i + 1;
pos11 = queryhl(1, 1, n, i);
pos22 = queryhr(1, 1, n, i);
// cout << pos1 << " " << pos11 << " " << pos22 << " " << pos2 << endl;
if(i == pos1 && pos2 == i)continue;
ll ret = 0;
if(pos1 <= pos11 && pos22 <= pos2){
ret = 1ll * (i - pos1 + 1) * (pos2 - i + 1) - 1ll * (i - pos11) * (pos22 - i);
}
else if(pos1 <= pos11){
ret = 1ll * (pos2 - i + 1) * (pos11 - pos1 + 1);
}
else if(pos22 <= pos2){
ret = 1ll * (i - pos1 + 1) * (pos2 - pos22 + 1);
}
// cout << ret << endl;
sum += ret;
}
printf("%lld\n", sum);
return 0;
}
Number Game2 title link
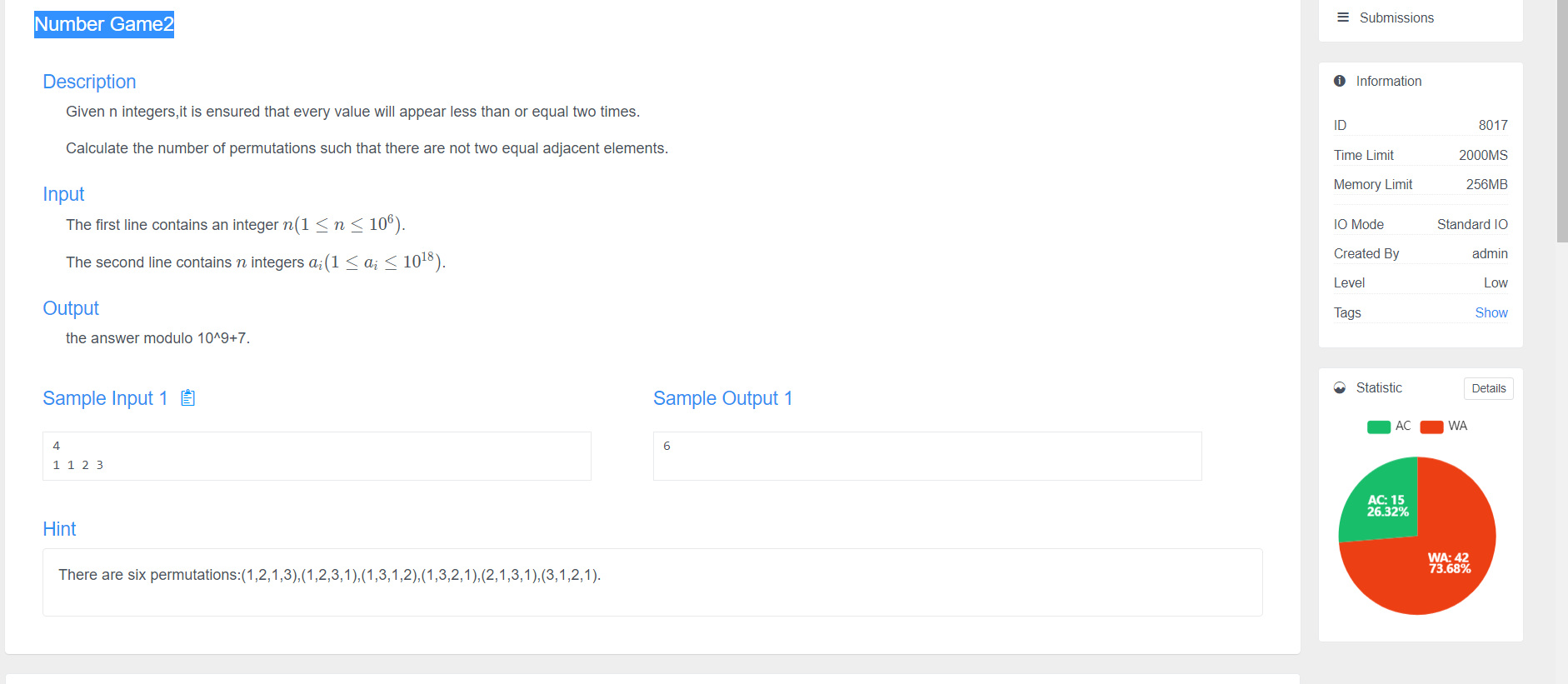
meaning of the title
N numbers, and the number of occurrences of each number is at most 2. Find all the permutations of the N numbers to meet the number of schemes in which any two adjacent numbers are different.
Problem solving ideas
Tolerance and rejection. First review high school mathematics

Then the answer is the total number of schemes - | at least one group of adjacent | + | at least two groups of adjacent | - | at least three groups of adjacent |
#include<bits/stdc++.h>
#include<stdlib.h>
#include<algorithm>
#include<stdio.h>
#include<string.h>
#include<queue>
#include<time.h>
#include <cstdio>
#include <iostream>
#include <vector>
#define ll long long
#define int long long
#define inf 0x3f3f3f3f
#define mods 1000000007
#define modd 998244353
#define PI acos(-1)
#define fi first
#define se second
#define lowbit(x) (x&(-x))
#define mp make_pair
#define pb push_back
#define si size()
#define E exp(1.0)
#define fixed cout.setf(ios::fixed)
#define fixeds(x) setprecision(x)
#define IOS ios::sync_with_stdio(false);cin.tie(0)
using namespace std;
ll gcd(ll a,ll b)
{
if(a<0)
a=-a;
if(b<0)
b=-b;
return b==0?a:gcd(b,a%b);
}
template<typename T>void read(T &res)
{
bool flag=false;
char ch;
while(!isdigit(ch=getchar()))
(ch=='-')&&(flag=true);
for(res=ch-48; isdigit(ch=getchar()); res=(res<<1)+(res<<3)+ch - 48)
;
flag&&(res=-res);
}
ll lcm(ll a,ll b)
{
return a*b/gcd(a,b);
}
ll qp(ll a,ll b,ll mod)
{
ll ans=1; //Fast power%
if(b==0)
{
return ans%mod;
}
while(b)
{
if(b%2==1)
{
b--;
ans=ans%mod*a%mod;
}
a=(a%mod*a%mod)%mod;
b=b/2;
}
return ans%mod;
}
ll qpn(ll a,ll b, ll p)
{
ll ans = 1; //Inverse element (numerator * QP (denominator, mod-2,mod))%mod;
a%=p;
while(b)
{
if(b&1)
{
ans = (ans*a)%p;
--b;
}
a =(a*a)%p;
b >>= 1;
}
return ans%p;
}
#define LL long long
/*N<=1e6,Using Fermat's small theorem*/
const int MX = 1000000 + 50;
const int mod = 1e9 + 7;
LL F[MX], invF[MX];
LL power(LL a, LL b)
{
LL ret = 1;
while(b)
{
if(b & 1)
ret = (ret * a) % mod;
a = (a * a) % mod;
b >>= 1;
}
return ret;
}
void init()
{
F[0] = 1;
for(int i = 1; i < MX; i++)
{
F[i] = (F[i - 1] * i) % mod;
}
invF[MX - 1] = power(F[MX - 1], mod - 2);
for(int i = MX - 2; i >= 0; i--)
{
invF[i] = (invF[i + 1]%mod * (i + 1) % mod)%mod; //invF[i]*i!=1,invF[i+1]*i!*(i+1)=1
}
}
LL C(int n, int m)
{
if(n < 0 || m < 0 || m > n)
return 0;
if(m == 0 || m == n)
return 1;
return (F[n]%mod * invF[n - m] % mod * invF[m] % mod)%mod;
}
LL A(int n, int m)
{
if(n < 0 || m < 0 || m > n)
return 0;
return F[n] * invF[n - m] % mod;
}
//ll vis[1000007];
unordered_map<ll,ll>vis;
signed main()
{
ll n;
read(n);
ll cnt=0;
for(int i=1; i<=n; i++)
{
ll x;
read(x);
// if(i%2==0)x--;
vis[x]++;
if(vis[x]==2)
cnt++;
}
ll le=n-2*cnt;
init();
ll ans=0;
// ll ans=(F[n]%mods*qp(qp(2,cnt,mods)%mods,mods-2,mods)%mods)%mods;
for(int i=0; i<=cnt; i++)
{
if(i%2)
{
// At least i types shall be placed adjacent
ll rnm=C(cnt,i)%mods; //* A(i,i)
ll now=n-i;// All remaining elements
ll ok=cnt-i;// Remaining duplicate groups
// Optional i types are bundled together
// ans=((ans+mods-rnm*(F[now]%mods*qp(qp(2,ok,mods)%mods,mods-2,mods)))%mods)%mods;
ll fuck=rnm%mods*F[now]%mods;
fuck=fuck%mods;
fuck=fuck*qp(qp(2,ok,mods),mods-2,mods)%mods;
ans=((ans-fuck)%mods+mods)%mods;
}
else
{
ll rnm=C(cnt,i)%mods; //* A(i,i)
ll now=n-i;// All remaining elements
ll ok=cnt-i;// Remaining duplicate groups
// Optional i types are bundled together
// ans=((ans+mods-rnm*(F[now]%mods*qp(qp(2,ok,mods)%mods,mods-2,mods)))%mods)%mods;
ll fuck=rnm%mods*F[now]%mods;
fuck=fuck%mods;
fuck=fuck*qp(qp(2,ok,mods),mods-2,mods)%mods;
ans=((ans+fuck)%mods)%mods;
}
}
printf("%lld",ans%mods);
}
SumMin title link
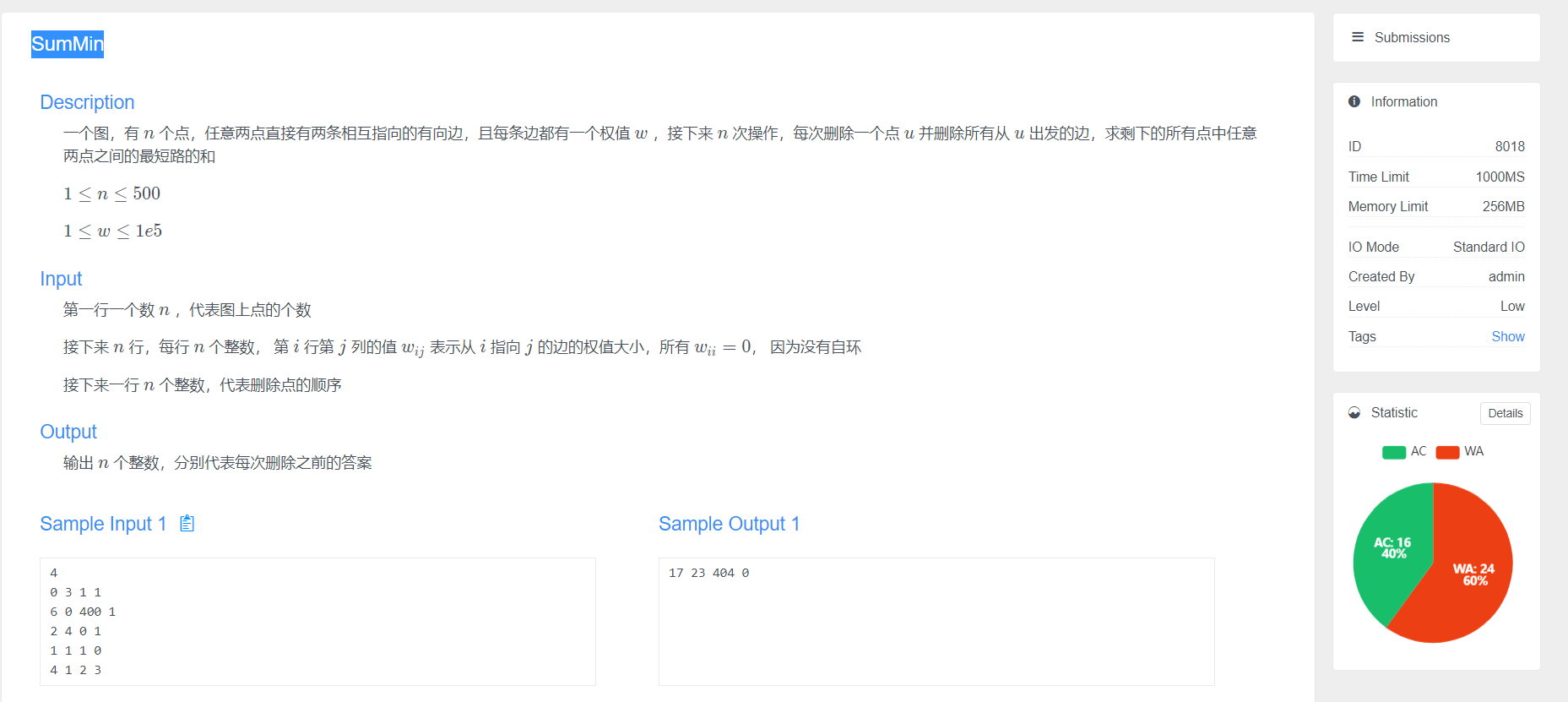
Considering the significance of floyd algorithm, the K-update of transfer point means to update the shortest path of the whole graph after adding K points in turn.
Then we think backwards, enumerate the deleted points backwards, add edges to the graph, and implement it with floyd.
ll G[550][550];
ll order[550];
ll ban[550];
vector<ll>s;
ll V[550][550];
signed main()
{
ll n;
read(n);
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
read(G[i][j]);
}
}
for(int i=1; i<=n; i++)
{
read(order[i]);
}
ll cnt=n;
for(int kk=n; kk>=1; kk--)
{
ll ans=0;
ll k=order[kk];
ban[k]=1;
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
// if(!ban[i]||!ban[j])continue;
if(G[i][k]+G[k][j]<G[i][j])
{
// ans=ans-G[i][j]+G[i][k]+G[k][j];
G[i][j]=G[i][k]+G[k][j];
}
}
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
if(ban[i]&&ban[j])
{
ans+=G[i][j];
}
}
}
s.push_back(ans);
}
for(int i=s.size()-1; i>=0; i--)
{
printf("%lld ",s[i]);
}
}
Merging of City Union joint search set + linear basis
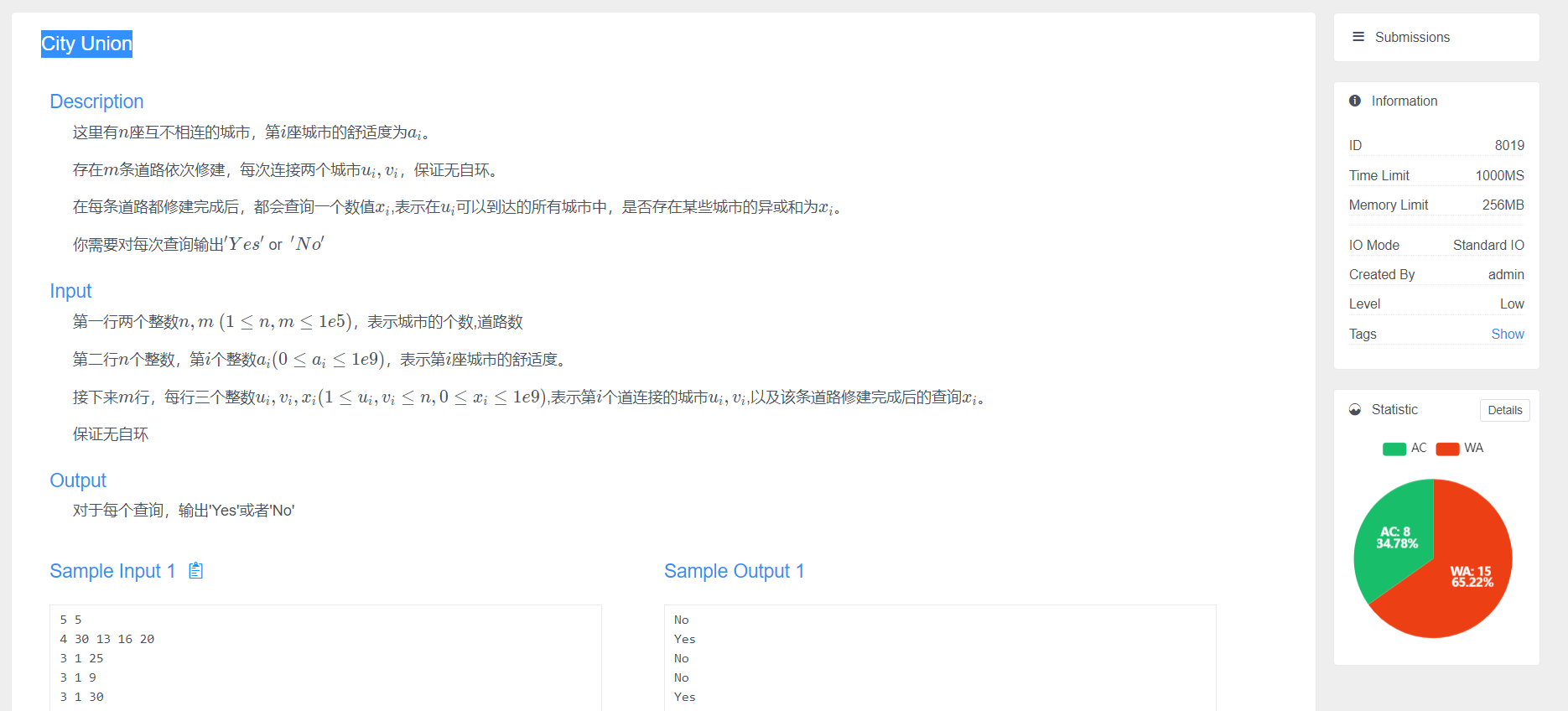
emmm is a very naked question, but I didn't do it. It seems that I didn't bring a linear base plate ((too little used)
Obviously, for a set, it is an obvious linear basis to query whether an X can be XOR by the numbers in the set.
We directly merge linear bases every time we add edges and merge and search the set. The merging of linear bases directly inserts one base into another base (violence). When querying ASK, it is analogized according to the way of insertion. If the insertion is not interrupted and the final inserted number x XOR is 0, it means that this x can be XOR.
#include<bits/stdc++.h>
#include<stdlib.h>
#include<algorithm>
#include<stdio.h>
#include<string.h>
#include<queue>
#include<time.h>
#include <cstdio>
#include <iostream>
#include <vector>
#define ll long long
#define int long long
#define inf 0x3f3f3f3f
#define mods 1000000007
#define modd 998244353
#define PI acos(-1)
#define fi first
#define se second
#define lowbit(x) (x&(-x))
#define mp make_pair
#define pb push_back
#define si size()
#define E exp(1.0)
#define fixed cout.setf(ios::fixed)
#define fixeds(x) setprecision(x)
#define IOS ios::sync_with_stdio(false);cin.tie(0)
using namespace std;
ll gcd(ll a,ll b)
{
if(a<0)
a=-a;
if(b<0)
b=-b;
return b==0?a:gcd(b,a%b);
}
template<typename T>void read(T &res)
{
bool flag=false;
char ch;
while(!isdigit(ch=getchar()))
(ch=='-')&&(flag=true);
for(res=ch-48; isdigit(ch=getchar()); res=(res<<1)+(res<<3)+ch - 48)
;
flag&&(res=-res);
}
ll lcm(ll a,ll b)
{
return a*b/gcd(a,b);
}
ll qp(ll a,ll b,ll mod)
{
ll ans=1; //Fast power%
if(b==0)
{
return ans%mod;
}
while(b)
{
if(b%2==1)
{
b--;
ans=ans%mod*a%mod;
}
a=(a%mod*a%mod)%mod;
b=b/2;
}
return ans%mod;
}
ll qpn(ll a,ll b, ll p)
{
ll ans = 1; //Inverse element (numerator * QP (denominator, mod-2,mod))%mod;
a%=p;
while(b)
{
if(b&1)
{
ans = (ans*a)%p;
--b;
}
a =(a*a)%p;
b >>= 1;
}
return ans%p;
}
ll p[100009][33];
inline void insert(ll x,ll pos)
{
for(ll i=32; i>=0; --i)
if((x>>i)&1)
{
if(!p[pos][i])
{
p[pos][i]=x;
break;
}
x^=p[pos][i];
}
}
inline void UN(ll x,ll y)
{
for(ll i=32; i>=0; --i)
if(p[x][i])
insert(p[x][i],y);
}
inline bool ask(ll pos,ll x)
{
for(ll i=32; i>=0; --i)
if((x>>i)&1)
{
if(!p[pos][i])
{
return false;
}
x^=p[pos][i];
}
if(x==0)
return true;
return false;
}
ll fa[100010];
ll find(ll x)
{
if(fa[x]==x)
return x;
return fa[x]=find(fa[x]);
}
ll a[100010];
signed main()
{
ll n,m;
read(n);
read(m);
for(int i=1; i<=n; i++)
{
read(a[i]);
fa[i]=i;
insert(a[i],i);
}
for(int i=1; i<=m; i++)
{
ll u,v,pp;
read(u);
read(v);
read(pp);
ll fu=find(u);
ll fv=find(v);
if(fu==fv)
{
if(ask(fu,pp))
{
printf("Yes\n");
continue;
}
printf("No\n");
continue;
}
ll rnm=max(fu,fv);
ll cnm=min(fu,fv);
fa[cnm]=rnm;
UN(cnm,rnm);
if(ask(rnm,pp))
{
printf("Yes\n");
continue;
}
printf("No\n");
continue;
}
}