background

treedp limit undirected edge, seemingly easy TLE dfs is second killed?
The problem done at the last second.

Title Description

Given a rootless tree, suppose it has n nodes with node numbers from 1 to N, find the sum of the distances from the N nodes 1-n to the other n-1 nodes.

input
The first line contains a positive integer n (n < = 100000), indicating the number of nodes.
The following (n - 1) lines, two integers per line, represent the edges of the tree.
output
Each line is an integer, and the i(i = 1,2,... n) line represents the sum of the distances from all nodes to the i-th point.

sample input
4
1 2
3 2
4 2

sample output
5
3
5
5

At first glance, this problem seems to be graph theory. Establish an undirected graph, then traverse each point, calculate the distance between it and each point, and output it.
But the data range is (n < = 100000), and the time complexity is O (n ²) Applied constant. So sure TLE, we gave up the idea.
How to optimize it?
In fact, it's easy to think of trees here. If we first find a root (the topic gives a rootless tree) and calculate the depth dep[i] of each point, the distance between u and V is abs (dep[u]-dep[v]). But the time complexity of this idea is also O (n ²) About, it may be to optimize a little constant and still TLE.

At this time, we think of the size [] array in the tree section, that is, the size of the subtree of a node in the tree.
What's the use of it? We find that in a tree without rings, many distances are repeated.
For example, if I want to calculate the distance from point u to point v, the distance from point v to its subtree already knows. If I calculate it again, it will be a waste of time.

Therefore, we record that size[i] represents the number of nodes (including I) in the subtree with I as the root node, and f[i] represents the sum of the distance from I to other points
For example, the following figure:

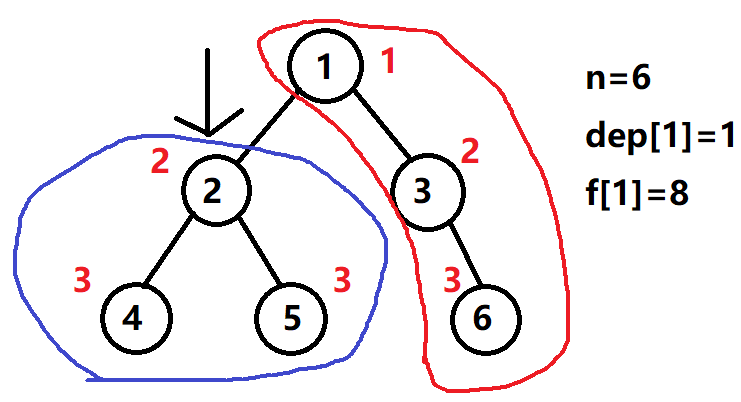
Suppose we take 1 as the root node, then f[1] can be calculated by the method of dep[i]-dep[1] above.
Now we visit node 2. We find that the distance from node 2 to other points is the distance from node 1 to other points, plus some "hands and feet". Through observation, we also found that for node 2, the distance from the point in the red area to node 1 is 1 more than that to node 1, while the distance from the point in the blue area to node 1 is 1 less than that to node 1.
At this time, size comes in handy. The number of nodes in the blue area is just size[i]. Is there anything special?
To sum up, f[i] = f[fa[i]] (distance from the original father to other sides) + n-size[i] (1 more node distance in the red area) - size[i] (1 less node distance in the blue area)

So it becomes treedp again...

Reference code:

#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
using namespace std;
struct node
{
	int x,y,next;
}a[210000];//Edge information 
int len,last[110000];
int n,f[110000],siz[110000],dep[110000];
//n represents the total number of nodes, f[i] represents the sum of the distance from node i to other points, siz[i] represents the number of nodes (including I itself) of the subtree with I as the root node, and dep[i] represents the depth of I 
void ins(int x,int y)//Jianbian 
{
	len++;
	a[len].x=x;a[len].y=y;a[len].next=last[x];
	last[x]=len;
}
void dfs1(int x)
{
	siz[x]=1;//The leaf node tree size is 1 
	for(int k=last[x] ; k!=-1 ; k=a[k].next)
	{
		int y=a[k].y;
		if(dep[y]==0)
		{
			dep[y]=dep[x]+1;
			dfs1(y);
			siz[x]+=siz[y];//Father plus the number of subtrees per son 
		}
	}
}
void dfs2(int x,int fa)//treedo 
{
	for(int k=last[x] ; k!=-1 ; k=a[k].next)
	{
		int y=a[k].y;
		if(y!=fa)//Remember to add this restriction 
		{
			f[y]=f[x]+(n-siz[y])-siz[y];//!  The essence! 
			dfs2(y,x);
		}
	}
}
signed main()
{
	len=0;memset(last,-1,sizeof(last));
	memset(dep,0,sizeof(dep));
	scanf("%lld",&n);
	for(int i=1 ; i<=n-1 ; i++)
	{
		int x,y;
		scanf("%lld %lld",&x,&y);
		ins(x,y);
		ins(y,x);//Rootless tree, two-way edge 
	}
	dep[1]=1;dfs1(1);//Take node 1 as the root node of the tree to find the depth of each point and the size of the subtree 
	for(int i=2 ; i<=n ; i++)f[1]+=dep[i]-dep[1];
	dfs2(1,1);
	for(int i=1 ; i<=n ; i++)printf("%lld\n",f[i]);
	return 0;
}

It seems to save a lot of time.