Briefly talking about some functions and applications of line segment tree
First, let's talk about the definition: line segment tree is a binary search tree. It divides an interval into several unit intervals, and each node stores an interval. It has powerful functions, supports interval summation, interval maximum, interval modification, single point modification and other operations.
Let's see a picture for you to understand. The video): 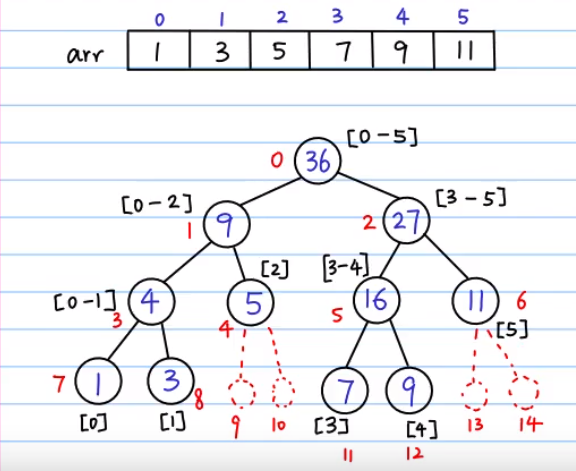
The red number in the figure represents the node subscript, and the range interval in brackets.
Line segment tree building:
void build_tree(int arr[], int tree[], int node, int left, int right){ //Establishing Segment Tree //Array is the original array, tree is the array of segment trees, node is the current node subscript, left,right is the interval range if(left == right){ //Start assignment recursively to leaf nodes tree[node] = arr[left]; } else { int left_node = 2 * node + 1;//The Node of Left Child int right_node = 2 * node + 2;//Right Child's Node int mid = (left + right) / 2; build_tree(arr, tree, left_node, left, mid);//Recursion from the left child build_tree(arr, tree, right_node, mid+1, right); tree[node] = tree[left_node] + tree[right_node]; //The root node equals the sum of the right and left children. } }
Line segment tree single point modification:
void update_tree(int arr[], int tree[], int node, int left, int right, int idx, int val){ //idx is the subscript of the value to be modified and val is the value to be changed if (left == right) {//Modify the value of the leaf node when it is recursive to the leaf node arr[idx] = val; tree[node] = val; } else { int mid = (left + right) / 2; int left_node = 2 * node + 1; int right_node = 2 * node + 2; if(idx >= left && idx <= mid) {//When the target node is in the left interval, it begins to recurse from the left child. update_tree(arr, tree, left_node, left, mid, idx, val); } else {//Otherwise, it starts with the right child. update_tree(arr, tree, right_node, mid+1, right, idx, val); } tree[node] = tree[left_node] + tree[right_node]; } }
Line segment tree interval query:
int query_tree(int tree[], int node, int left, int right, int L, int R) { //L and R are the range of intervals to be queried if(R < left ||L > right) {//Out of range return 0; } else if (L <= left && R >= right){//When it happens to be within the query range, it returns the value of the node directly. return tree[node]; } else { int mid = (left + right) / 2; int left_node = 2 * node + 1; int right_node = 2 * node + 2; int sum_left = query_tree(tree, left_node, left, mid, L, R);//Recursive Left Child int sum_right = query_tree(tree, right_node, mid+1, right, L, R);//Recursive Right Child return sum_left + sum_right;//Add up the left and right children to update the value of the root node } }
When we need interval modification, if we traverse to the leaf node every time and then modify the value, it will obviously waste a lot of time.
So we can use the idea of lazy labeling: the meaning of labeling: the interval has been updated, but the sub-interval has not been updated, what is the updated information (interval summation only records have been accessed, and interval addition, subtraction, multiplication and division and other operations to record what kind of operation is carried out)
After the laziness tag is downloaded, that is, the download tag: as the name implies, the download tag is to pass a node's laziness tag to its left and right sons, and then delete the node's laziness tag.
Functions that download lazy tags (add value on the original basis):
void pushdown(int tree[], int left, int right, int node) { if(lazy[node]) { int left_node = 2 * node + 1; int right_node = 2 * node + 2; lazy[left_node] += lazy[node]; lazy[right_node] += lazy[node]; int mid = (left + right) / 2; tree[left_node] += (mid - left + 1) * lazy[node];//Note that the assignment here is multiplied by the lazy marker of the parent node. //Because laziness tags may be downloaded by parent nodes many times, multiplying their own laziness tags may lead to repeated computation. tree[right_node] += (right - mid) * lazy[node]; lazy[node] = 0; } }
Functions that download lazy tags (changes):
void pushdown(int tree[], int left, int right, int node) { if(lazy[node]) { int left_node = 2 * node + 1; int right_node = 2 * node + 2; lazy[left_node] = lazy[node]; lazy[right_node] = lazy[node]; int mid = (left + right) / 2; tree[left_node] = (mid - left + 1) * lazy[node]; tree[right_node] = (right - mid) * lazy[node]; lazy[node] = 0; } }
Line segment tree interval + val code:
void area_update_tree(int tree[], int node, int left, int right, int L, int R, int val) { if (left >=L && right <= R) { tree[node] += (right - left + 1) * val; lazy[node] += val; return;//According to lazy's idea, since there is no need to traverse to the lower nodes, there is no need to continue updating downwards and return directly. } pushdown(tree, left, right, node);//Pass the updated information of the current node to the next layer (its left and right son nodes) int mid = (left + right) / 2; int left_node = 2 * node + 1; int right_node = 2 * node + 2; if(L <= mid) area_update_tree(tree, left_node, left, mid, L, R, val); if(R > mid) area_update_tree(tree, right_node, mid + 1, right, L, R, val); tree[node] = tree[left_node] + tree[right_node]; }
Interval modification (modification):
void area_update_tree(int tree[], int node, int left, int right, int L, int R, int val if (left >=L && right <= R) { tree[node] = (right - left + 1) * val; lazy[node] = val; return; } pushdown(tree, left, right, node); int mid = (left + right) / 2; int left_node = 2 * node + 1; int right_node = 2 * node + 2; if(L <= mid) area_update_tree(tree, left_node, left, mid, L, R, val); if(R > mid) area_update_tree(tree, right_node, mid + 1, right, L, R, val); tree[node] = tree[left_node] + tree[right_node]; }