Quick sort

definition:

• Quick sort is an improvement of bubble sort. Its basic idea is to divide the data to be sorted into two independent parts through one-time sorting. All the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method. The whole sorting process can be recursive, so that the whole data becomes an ordered sequence.

Sorting principle:

1. First, set a boundary value, and divide the array into left and right parts through the boundary value;
2. Put the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, all elements in the left part are less than or equal to the boundary value, while all elements in the right part are greater than or equal to the boundary value;
3. Then, the data on the left and right can be sorted independently. For the array data on the left, you can take another boundary value and divide this part of the data into left and right parts. Similarly, place the smaller value on the left and the larger value on the right. The array data on the right can also be processed similarly.
4. By repeating the above process, we can see that this is a recursive definition. After the left part is sorted recursively, the right part is sorted recursively. When the left and right parts of the array are sorted, the whole data is also sorted.
   
   

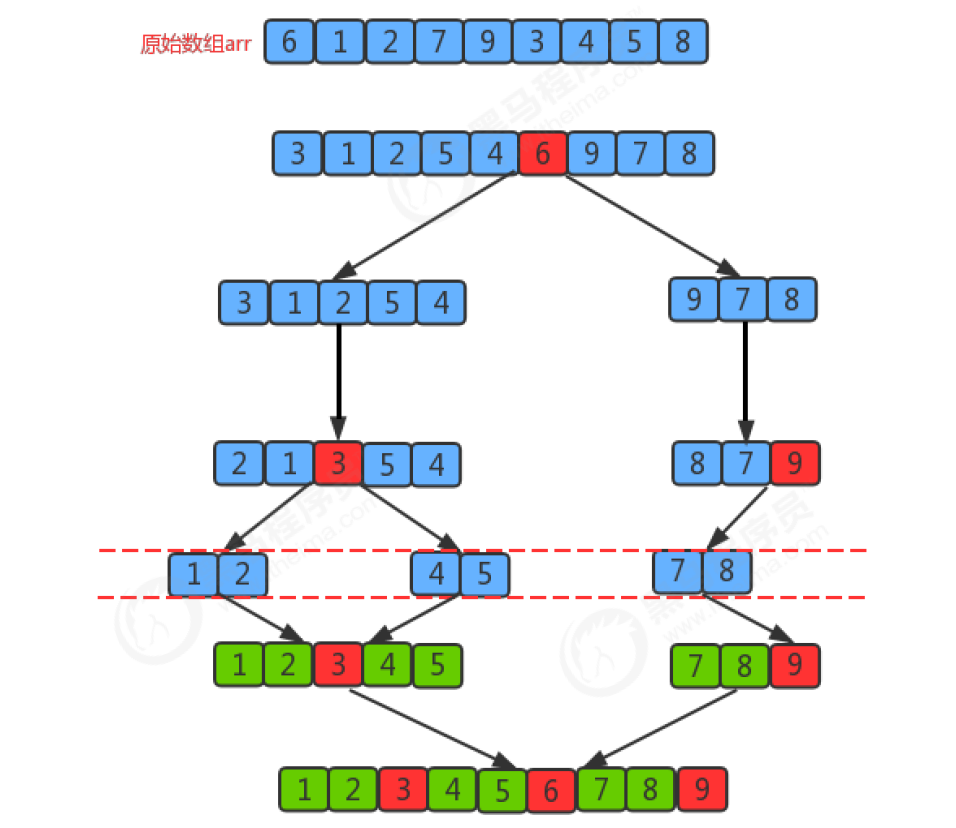
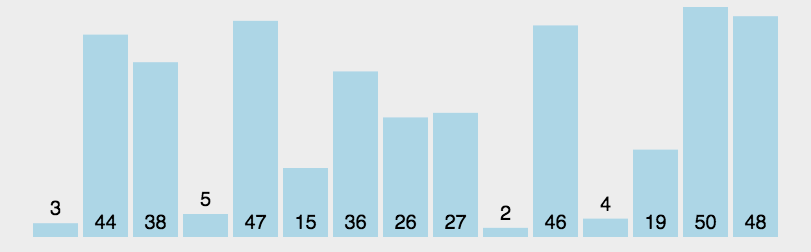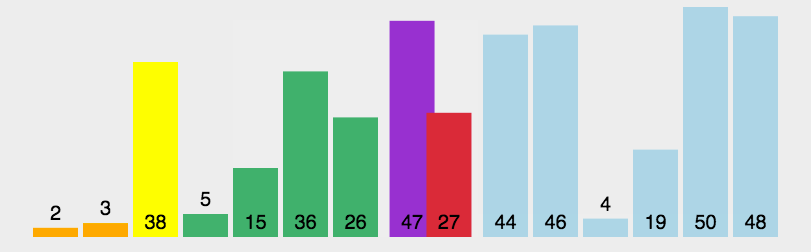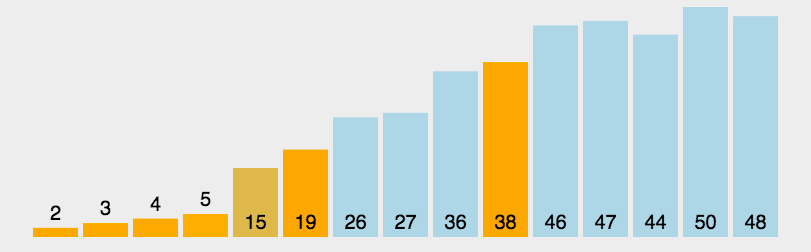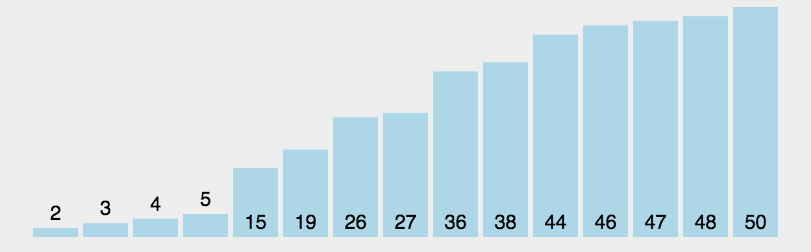
Segmentation principle:

Quick sort is also a sort algorithm with divide and conquer idea

The basic idea of dividing an array into two subarrays:

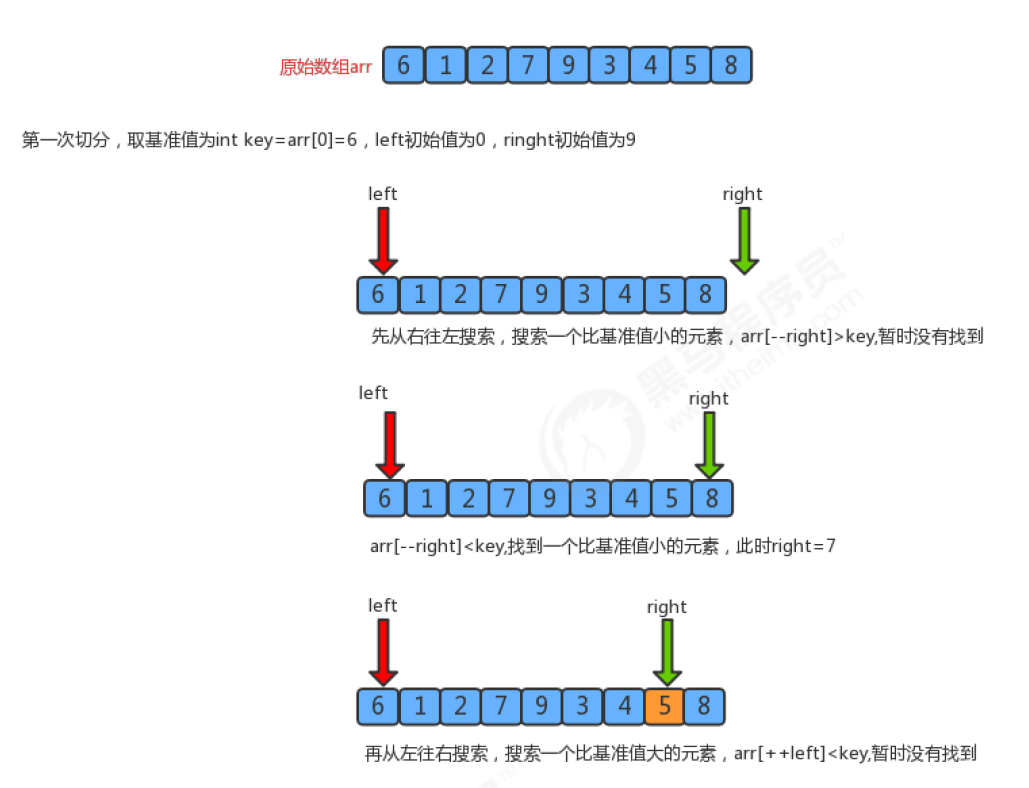
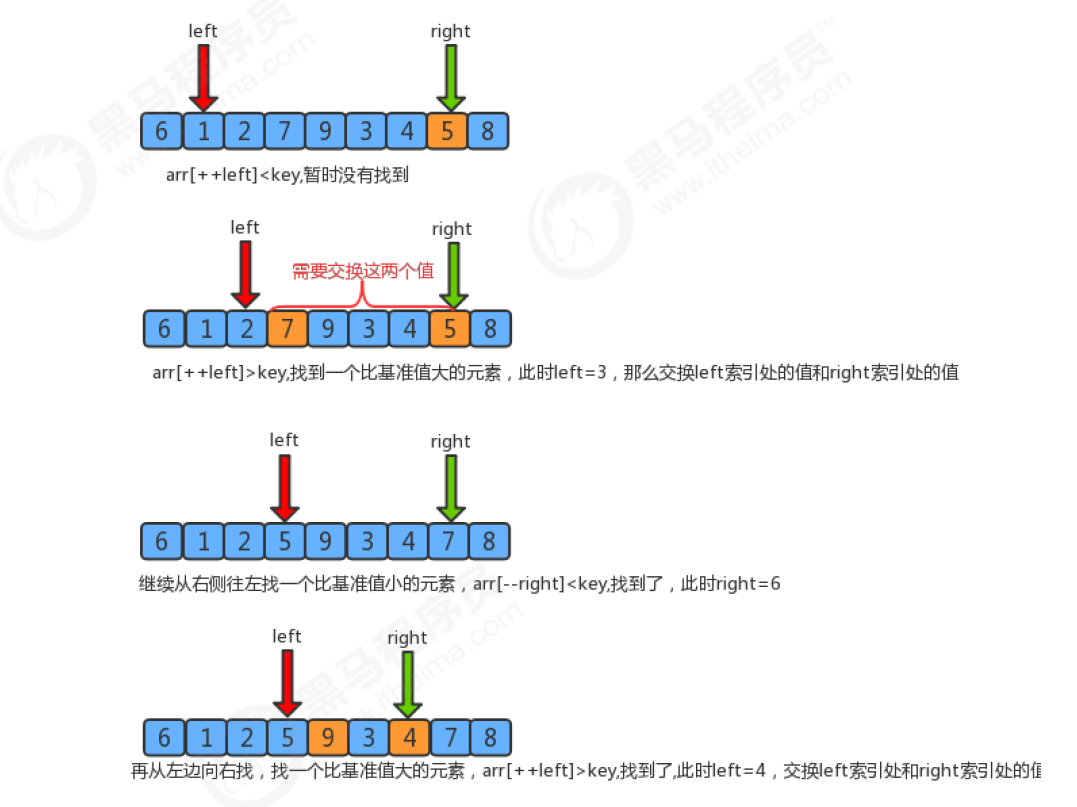
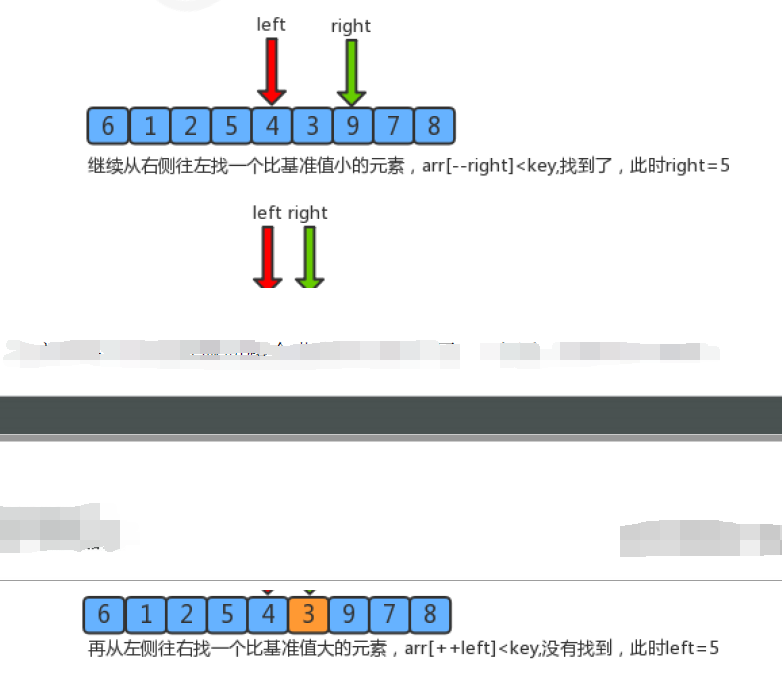
1. Find a reference value and point to the head and tail of the array with two pointers respectively;
2. First, search for an element smaller than the reference value from the tail to the head, stop the search, and record the position of the pointer;
3. Then, search for an element larger than the reference value from the head to the tail, stop when the search is found, and record the position of the pointer;
4. Exchange the elements of the current left pointer position and the right pointer position;
5. Repeat steps 2, 3 and 4 until the value of the left pointer is greater than that of the right pointer.
   
   
   
   
   

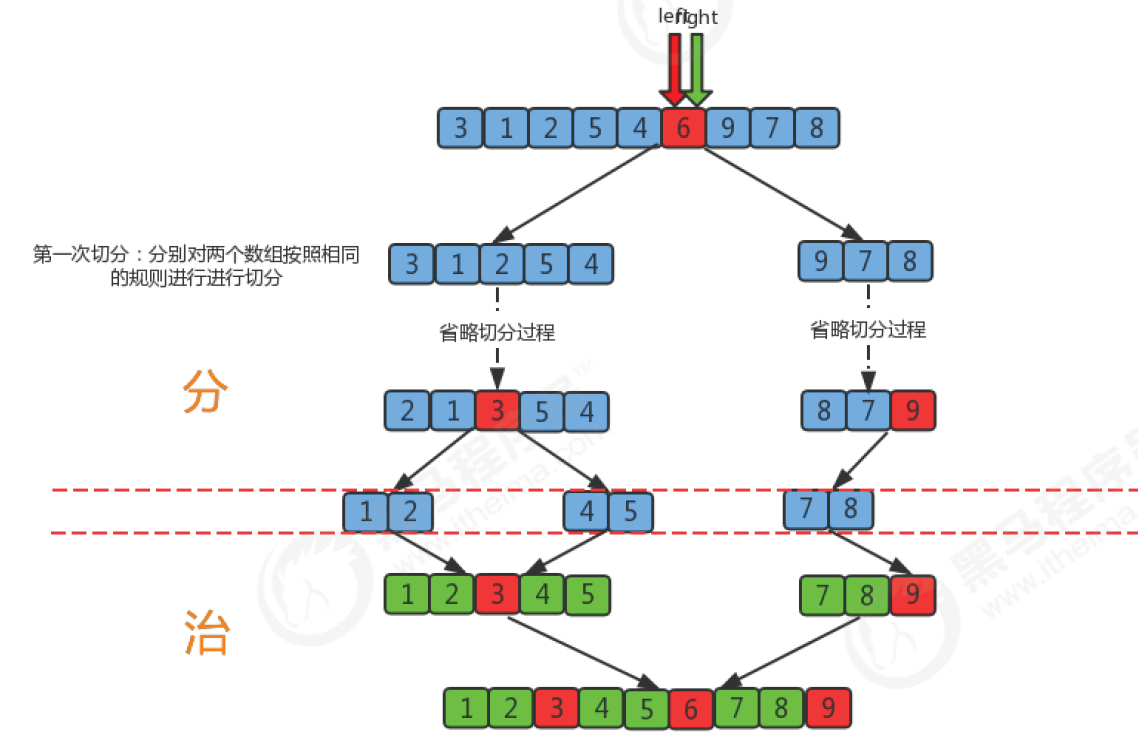
Code implementation 1

Quicksort API design:

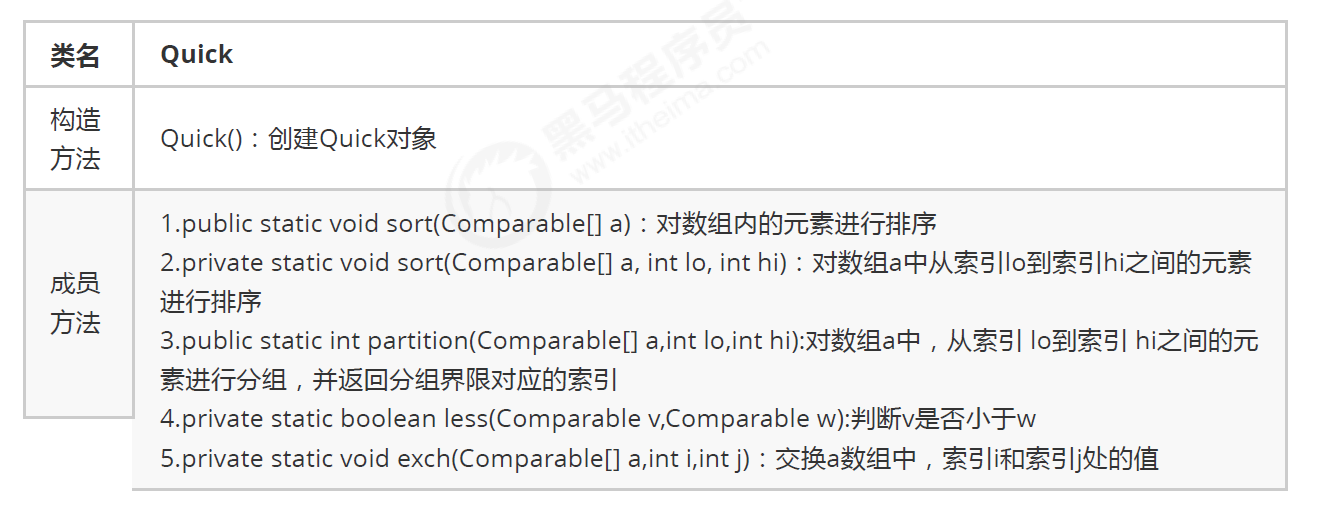
code

public class Quick {
    /*
    Compare whether the v element is smaller than the w element
 */
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }

    /*
   Array elements i and j swap positions
    */
    private static void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }

    //Sort the elements in the array
    public static void sort(Comparable[] a) {
        int lo = 0;
        int hi = a.length-1;
        sort(a,lo,hi);
    }

    //Sorts the elements in array a from index lo to index hi
    private static void sort(Comparable[] a, int lo, int hi) {
        //Security verification
        if (hi<=lo){
            return;
        }

        //The elements from lo index to hi index in the array need to be grouped (left subgroup and right subgroup);
        int partition = partition(a, lo, hi);//Returns the index of the boundary value of the group, and the index after the boundary value position transformation

        //Order the left subgroup
        sort(a,lo,partition-1);

        //Order the right subgroup
        sort(a,partition+1,hi);
    }

    //Group the elements in array a from index lo to index hi, and return the index corresponding to the grouping boundary
    public static int partition(Comparable[] a, int lo, int hi) {
        //Determine boundary value
        Comparable key = a[lo];
        //Define two pointers to point to the next position at the minimum index and the maximum index of the element to be segmented
        int left=lo;
        int right=hi+1;

        //segmentation
        while(true){
            //First scan from right to left, move the right pointer, find an element with a smaller or equal score boundary value, and stop
            while(less(key,a[--right])){
                if (right==lo){
                    break;
                }
            }

            //Scan from left to right, move the left pointer, find an element with a score boundary value greater or equal, and stop
            while(less(a[++left],key)){
                if (left==hi){
                    break;
                }
            }
            //Judge left > = right. If yes, it proves that the element scanning is completed and ends the cycle. If not, it can exchange elements
            if (left>=right){ // It must be left > = right, because left may be greater than right
                break;
            }else{
                exch(a,left,right);
            }
        }

        //Exchange boundary value
        exch(a,lo,right); //At this time, you can only exchange values with right, because it is possible that left is greater than right

        return right;
    }

}

Test:

 public static void main(String[] args) {
        Integer[] data = { 6, 1,6, 2, 7, 9, 3, 4, 5,6, 8 };
        System.out.println("Before sorting:\n" + java.util.Arrays.toString(data));
        Quick.sort(data);
        System.out.println("After sorting:\n" + java.util.Arrays.toString(data));
    }

Code implementation 2

/**
 * Quick sort
 * The records to be sorted are divided into two independent parts through one-time sorting. The keywords of some records are smaller than those of the other,
 * Then continue sorting the two parts respectively until the whole sequence is in order.
 * @author shkstart
 * 2018-12-17
 */
public class QuickSort {

    private static void swap(int[] data, int i, int j) {
        int temp = data[i];
        data[i] = data[j];
        data[j] = temp;
    }

    public static void quickSort(int[] data){
        subSort(data,0,data.length-1);
    }

    private static void subSort(int[] data, int start, int end) {
        if (start < end) {
            int base = data[start];
            int low = start;
            int high = end + 1;
            while (true) {
                while (low < end && data[++low] - base <= 0)
                    ;
                while (high > start && data[--high] - base >= 0)
                    ;
                if (low < high) {
                    swap(data, low, high);
                } else {
                    break;
                }
            }
            swap(data, start, high);

            subSort(data, start, high - 1);//Recursive call
            subSort(data, high + 1, end);
        }
    }



    public static void main(String[] args) {
        int[] data = { 9, -16, 30, 23, -30, -49, 25, 21, 30 };
        System.out.println("Before sorting:\n" + java.util.Arrays.toString(data));
        quickSort(data);
        System.out.println("After sorting:\n" + java.util.Arrays.toString(data));
    }
}

Sort lines:

import main.java.Algorithms.DataWrap;

public class QuickSort02 {
    private static void swap(DataWrap[] data, int i, int j) {
        DataWrap temp = data[i];
        data[i] = data[j];
        data[j] = temp;
    }

    private static void subSort(DataWrap[] data, int start, int end) {
        if (start < end) {
            DataWrap base = data[start];
            int i = start;
            int j = end + 1;
            while (true) {
                while (i < end && data[++i].compareTo(base) <= 0)
                    ;
                while (j > start && data[--j].compareTo(base) >= 0)
                    ;
                if (i < j) {
                    swap(data, i, j);
                } else {
                    break;
                }
            }
            swap(data, start, j);
            subSort(data, start, j - 1);
            subSort(data, j + 1, end);
        }
    }
    public static void quickSort(DataWrap[] data){
        subSort(data,0,data.length-1);
    }
    public static void main(String[] args) {
        DataWrap[] data = { new DataWrap(9, ""), new DataWrap(-16, ""),
                new DataWrap(21, "*"), new DataWrap(23, ""),
                new DataWrap(-30, ""), new DataWrap(-49, ""),
                new DataWrap(21, ""), new DataWrap(30, "*"),
                new DataWrap(30, "") };
        System.out.println("Before sorting:\n" + java.util.Arrays.toString(data));
        quickSort(data);
        System.out.println("After sorting:\n" + java.util.Arrays.toString(data));
    }
}

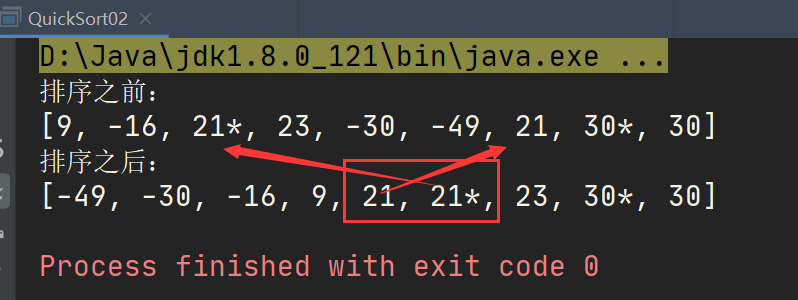
Quick sort is unstable

• Quick sort requires a benchmark value. Find an element smaller than the benchmark value on the right side of the benchmark value and an element larger than the benchmark value on the left side of the benchmark value, and then exchange the two elements. At this time, the stability will be destroyed. Therefore, quick sort is an unstable algorithm.

Quick sort time complexity analysis:

The first segmentation of quick sorting starts from both ends and searches alternately until left and right coincide. Therefore, the time complexity of the first segmentation algorithm is O(n)

However, the time complexity of the whole quick sort is related to the number of segmentation.

Best case:

The reference number selected for each segmentation just divides the current sequence equally.

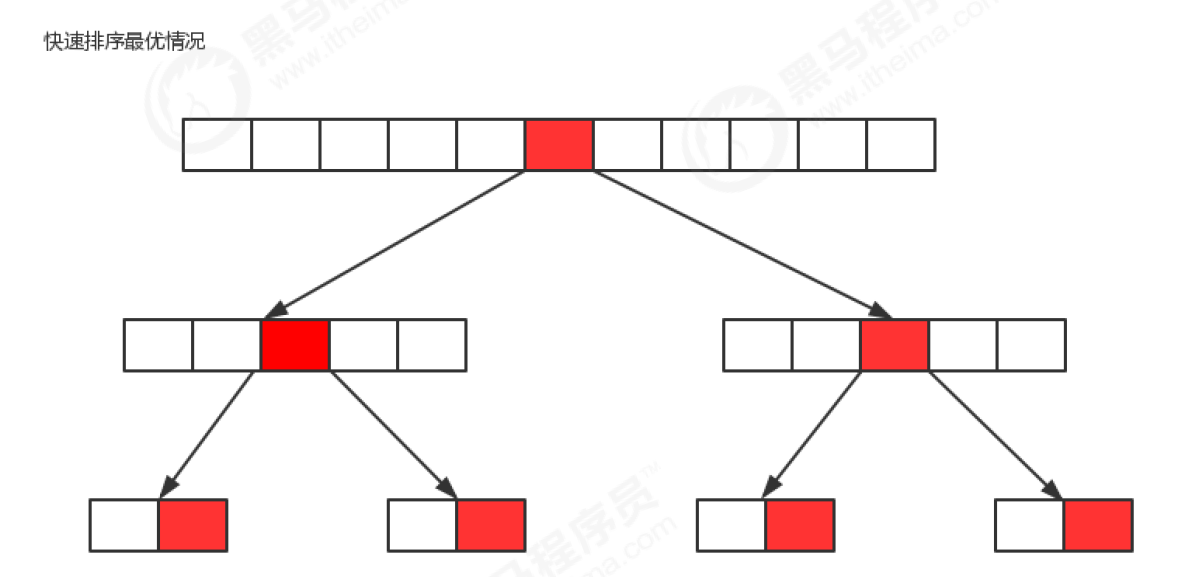
• If we regard the segmentation of an array as a tree, the above figure is the diagram of its optimal situation, which has been segmented logn times. Therefore, the time complexity of quick sorting in the optimal situation is O(nlogn);

Worst case scenario:

• The benchmark number selected for each segmentation is the maximum number or the minimum number in the current sequence, so that each segmentation will have a subgroup, so it will be segmented n times in total. Therefore, in the worst case, the time complexity of quick sorting is O(n^2);
  
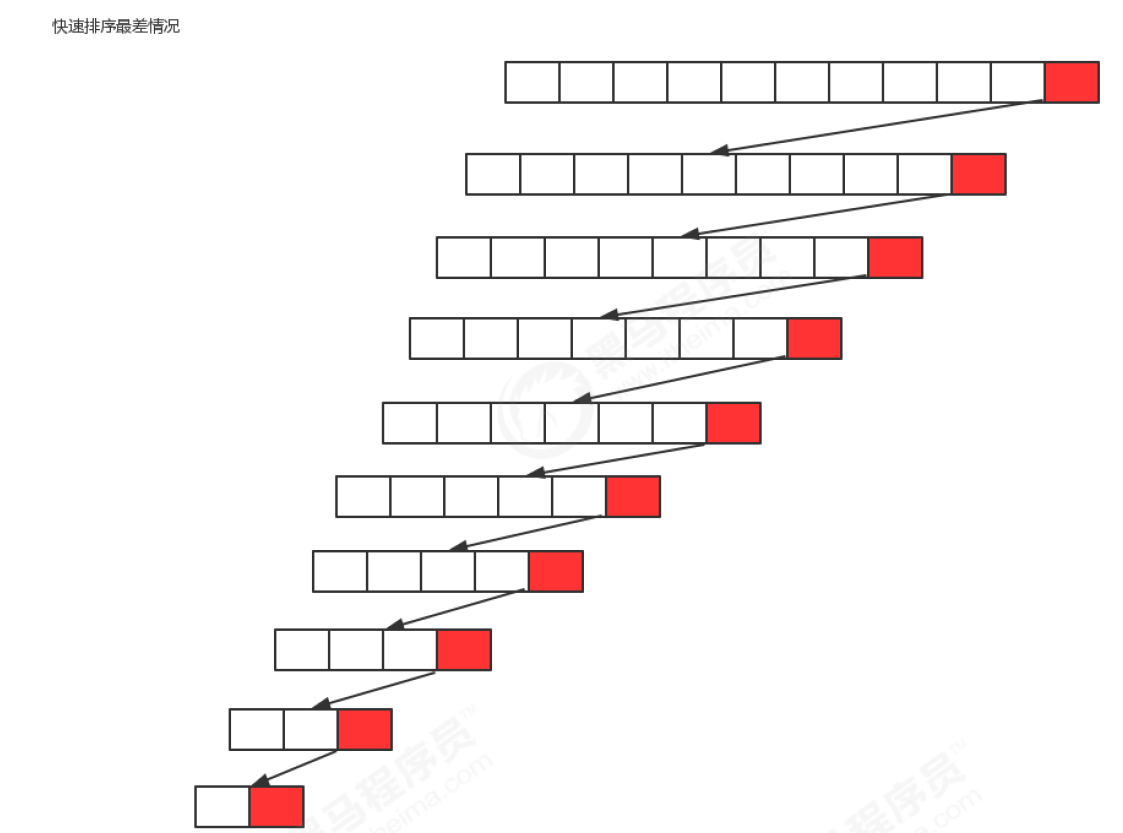
  In the worst case, the time complexity of quick sort is O(n^2);

Average:

• In this case, we can also prove by mathematical induction that the time complexity of quick sorting is O(nlogn),

The average time complexity of quick sorting is O(nlogn),

Summary:

• Best case: T(n) = O(nlogn)
• Worst case: T(n) = O(n2)
• Average case: T(n) = O(nlogn) unstable