Let's start with tracking:

Target tracking is divided into single target tracking and multi-target tracking

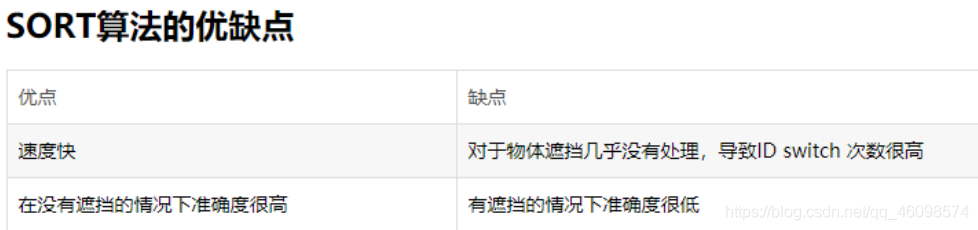
Single target tracking frames a single target on the initial frame of the video, and predicts the size and position of the target in the subsequent frames. Typical algorithms include Mean shift (state prediction with Kalman filter and particle filter), TLD (tracking based on online learning), KCF (correlation filter), etc.

Many tracking algorithms are built in libraries such as Opencv. KCF is a classic single target tracking algorithm. The speed is not very fast, but the accuracy is good

Unlike single target tracking, multi-target tracking first frames a single target on the initial frame, but tracks the size and position of multiple targets, and the number and position of targets in each frame may change. In addition, there are the following problems in multi-target tracking:

Deal with the emergence of new targets and the disappearance of old targets;

Motion prediction and similarity discrimination of tracking targets, that is, the matching of targets in the previous frame and the next frame;

Overlap and occlusion between tracking targets;

Re recognition of the reappearance of a tracking target after it has been lost for a period of time.

What are the solutions to this situation? The following is a comprehensive description.

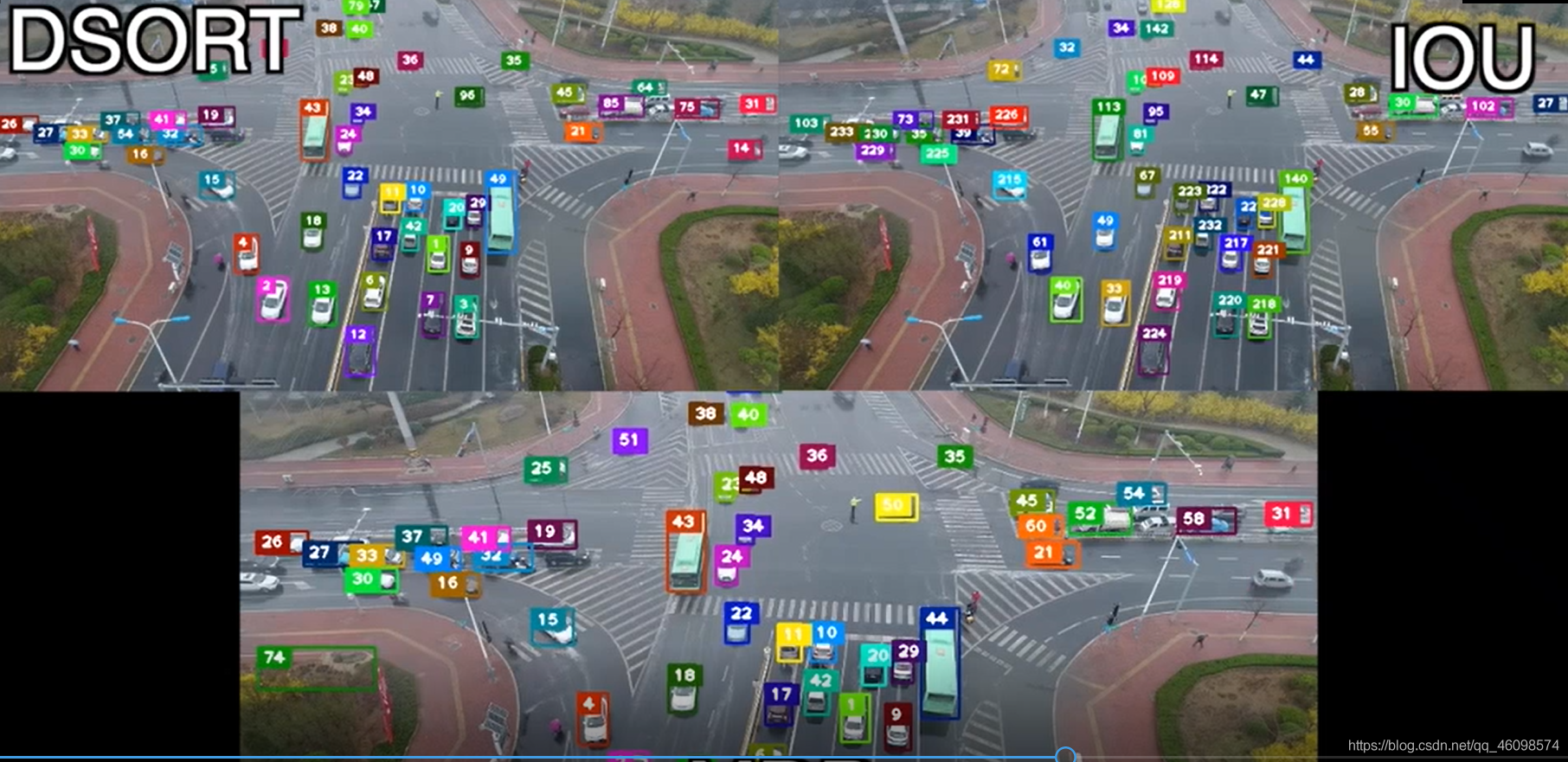
Before tracking, all targets have been detected and the feature modeling process has been realized. 1 when the first frame comes in, initialize and create a new tracker with the detected target and mark the id. 2 when the next frame comes in, first go to the Kalman filter to get the state prediction and covariance prediction generated by the previous frame box. Calculate the IOU of all target state predictions of the tracker and the box detected in this frame, obtain the maximum unique matching of IOU (data association part) through the Hungarian Assignment algorithm, and then remove the matching value less than iou_threshold matching. 3 use the matched target detection box in this frame to update the Kalman tracker, calculate the Kalman gain, state update and covariance update, and output the state update value as the tracking box of this frame. Reinitialize the tracker for targets that do not match in this frame.

Among them, the Kalman tracker combines the historical tracking records to adjust the residual between the historical box and the current box to better match the tracking id.

SORT's contribution mainly includes three aspects:
The detection results of powerful CNN detector are used for multi-target tracking

The method based on Kalman filter and Hungarian algorithm is used for tracking

Open source code provides a new baseline for MOT field

SORT improves this two-stage matching algorithm into a one-stage method, and can be tracked online.

Specifically, SORT introduces the linear velocity model and Kalman filter to predict the position. When there is no suitable matching detection frame, it uses the motion model to predict the position of the object.

SORT

from __future__ import print_function
 
from numba import jit      #Is a JIT Library of python, which realizes runtime acceleration through decorator
import os.path
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches  #Used to draw common images (such as rectangle, ellipse, circle, polygon)
from skimage import io
from sklearn.utils.linear_assignment_ import linear_assignment
import glob
import time
import argparse
from filterpy.kalman import KalmanFilter  #filterpy contains some libraries of common filters
 
@jit  #jit decorator is used to speed up the calculation of for loop
def iou(bb_test,bb_gt):
  """
  Computes IOU between two bboxes in the form [x1,y1,x2,y2]
  """
  xx1 = np.maximum(bb_test[0], bb_gt[0])
  yy1 = np.maximum(bb_test[1], bb_gt[1])
  xx2 = np.minimum(bb_test[2], bb_gt[2])
  yy2 = np.minimum(bb_test[3], bb_gt[3])
  w = np.maximum(0., xx2 - xx1)
  h = np.maximum(0., yy2 - yy1)
  wh = w * h
  o = wh / ((bb_test[2]-bb_test[0])*(bb_test[3]-bb_test[1])   #IOU = (area of intersection between bb_test and bb_gt boxes) / (area of bb_test box + area of bb_gt box - area of intersection between them)
    + (bb_gt[2]-bb_gt[0])*(bb_gt[3]-bb_gt[1]) - wh)
  return(o)
 
def convert_bbox_to_z(bbox): #Change bbox from [x1,y1,x2,y2] to [frame center point x, frame center point y, frame area s, width height ratio r]^T
  """
  Takes a bounding box in the form [x1,y1,x2,y2] and returns z in the form
    [x,y,s,r] where x,y is the centre of the box and s is the scale/area and r is
    the aspect ratio
  """
  w = bbox[2]-bbox[0]
  h = bbox[3]-bbox[1]
  x = bbox[0]+w/2.
  y = bbox[1]+h/2.
  s = w*h    #scale is just area
  r = w/float(h)
  return np.array([x,y,s,r]).reshape((4,1))  #Convert the array to 4 rows and 1 column, i.e. [x,y,s,r]^T
 
def convert_x_to_bbox(x,score=None): #Convert bbox in the form of [x,y,s,r] to the form of [x1,y1,x2,y2]
  """
  Takes a bounding box in the centre form [x,y,s,r] and returns it in the form
    [x1,y1,x2,y2] where x1,y1 is the top left and x2,y2 is the bottom right
  """
  w = np.sqrt(x[2]*x[3])  #w=sqrt(w*h * w/h)
  h = x[2]/w              #h=w*h/w
  if(score==None): #If the test box does not have confidence
    return np.array([x[0]-w/2.,x[1]-h/2.,x[0]+w/2.,x[1]+h/2.]).reshape((1,4))  #Return [x1,y1,x2,y2]
  else:            #If the test frame has confidence
    return np.array([x[0]-w/2.,x[1]-h/2.,x[0]+w/2.,x[1]+h/2.,score]).reshape((1,5)) #Return [x1,y1,x2,y2,score]
 
 
class KalmanBoxTracker(object):
  """
  This class represents the internel state of individual tracked objects observed as bbox.
  """
  count = 0
  def __init__(self,bbox):
    """
    Initialises a tracker using initial bounding box.  Initialize the tracker using the initial bounding box
    """
    #define constant velocity model                #Define uniform velocity model
    self.kf = KalmanFilter(dim_x=7, dim_z=4)       #The state variable is 7-dimensional and the observation value is 4-dimensional. Build the target according to the required dimension
    self.kf.F = np.array([[1,0,0,0,1,0,0],[0,1,0,0,0,1,0],[0,0,1,0,0,0,1],[0,0,0,1,0,0,0],[0,0,0,0,1,0,0],[0,0,0,0,0,1,0],[0,0,0,0,0,0,1]])
    self.kf.H = np.array([[1,0,0,0,0,0,0],[0,1,0,0,0,0,0],[0,0,1,0,0,0,0],[0,0,0,1,0,0,0]])
 
    self.kf.R[2:,2:] *= 10.
    self.kf.P[4:,4:] *= 1000. #give high uncertainty to the unobservable initial velocities
    self.kf.P *= 10.          # The default defined covariance matrix is NP Eye (dim_x) multiplies the value in P by 101000 to assign uncertainty
    self.kf.Q[-1,-1] *= 0.01
    self.kf.Q[4:,4:] *= 0.01
 
    self.kf.x[:4] = convert_bbox_to_z(bbox)  #Convert bbox into the form of [x,y,s,r]^T and assign it to the first four bits of state variable X
    self.time_since_update = 0
    self.id = KalmanBoxTracker.count
    KalmanBoxTracker.count += 1
    self.history = []
    self.hits = 0
    self.hit_streak = 0
    self.age = 0
 
  def update(self,bbox):
    """
    Updates the state vector with observed bbox.
    """
    self.time_since_update = 0
    self.history = []
    self.hits += 1
    self.hit_streak += 1
    self.kf.update(convert_bbox_to_z(bbox))
 
  def predict(self):
    """
    Advances the state vector and returns the predicted bounding box estimate.
    """
    if((self.kf.x[6]+self.kf.x[2])<=0):
      self.kf.x[6] *= 0.0
    self.kf.predict()
    self.age += 1
    if(self.time_since_update>0):
      self.hit_streak = 0
    self.time_since_update += 1
    self.history.append(convert_x_to_bbox(self.kf.x))
    return self.history[-1]
 
  def get_state(self):
    """
    Returns the current bounding box estimate.
    """
    return convert_x_to_bbox(self.kf.x)
 
def associate_detections_to_trackers(detections,trackers,iou_threshold = 0.3):  #Used to associate detection with tracking
  """
  Assigns detections to tracked object (both represented as bounding boxes)
  Returns 3 lists of matches, unmatched_detections and unmatched_trackers
  """
  if(len(trackers)==0):  #If the tracker is empty
    return np.empty((0,2),dtype=int), np.arange(len(detections)), np.empty((0,5),dtype=int)
  iou_matrix = np.zeros((len(detections),len(trackers)),dtype=np.float32) # Detector and tracker IOU matrix
 
  for d,det in enumerate(detections):
    for t,trk in enumerate(trackers):
      iou_matrix[d,t] = iou(det,trk)   #Calculate the IOU of detector and tracker and assign it to the corresponding position of IOU matrix
  matched_indices = linear_assignment(-iou_matrix)    # reference resources: https://blog.csdn.net/herr_kun/article/details/86509591 The minus sign is because linear_assignment seeks the minimum cost combination, and what we need is the maximum combination of IOU, so we take the minus sign
 
  unmatched_detections = []    #Detector on unmatched
  for d,det in enumerate(detections):
    if(d not in matched_indices[:,0]):  #If the d-th detection result in the detector is not in the matching result index, D does not match
      unmatched_detections.append(d)
  unmatched_trackers = []      #Tracker on unmatched
  for t,trk in enumerate(trackers):
    if(t not in matched_indices[:,1]):  #If the t-th tracking result in the tracker is not in the matching result index, t does not match
      unmatched_trackers.append(t)
 
  #filter out matched with low IOU
  matches = []  #Store the filtered matching results
  for m in matched_indices:   #Traversal rough matching result
    if(iou_matrix[m[0],m[1]]<iou_threshold):   #m[0] is the detector ID and m[1] is the tracker ID. if their IOU is less than the threshold, they are regarded as not matched successfully
      unmatched_detections.append(m[0])
      unmatched_trackers.append(m[1])
    else:
      matches.append(m.reshape(1,2))          #Change the filtered matching pair dimension into 1x2 form
  if(len(matches)==0):           #If the filtered matching result is empty, an empty matching result will be returned
    matches = np.empty((0,2),dtype=int)  
  else:                          #If the filtered matching result is not empty, continue to add matching pairs according to the direction of 0 axis
    matches = np.concatenate(matches,axis=0)
 
  return matches, np.array(unmatched_detections), np.array(unmatched_trackers)  #The tracker array has 5 columns (the last column is ID)
 
 
 
class Sort(object):
  def __init__(self,max_age=1,min_hits=3):
    """
    Sets key parameters for SORT
    """
    self.max_age = max_age
    self.min_hits = min_hits
    self.trackers = []
    self.frame_count = 0
 
  def update(self,dets):  #The input is the form of test result [x1,y1,x2,y2,score]
    """
    Params:
      dets - a numpy array of detections in the format [[x1,y1,x2,y2,score],[x1,y1,x2,y2,score],...]
    Requires: this method must be called once for each frame even with empty detections.   #Every frame has to be called once, even if the detection result is empty
    Returns the a similar array, where the last column is the object ID.                    #Returns a similar array, and the last column is the target ID
    NOTE: The number of objects returned may differ from the number of detections provided.  #The number of returned targets may be different from the number of tests provided
    """
    self.frame_count += 1   #Frame count
    #get predicted locations from existing trackers.
    trks = np.zeros((len(self.trackers),5)) # Create a two-dimensional zero matrix according to the current number of all Kalman trackers. The dimension is: number of Kalman tracker IDS x 5 (these five columns are bbox and ID)
    to_del = []                             #Save to be deleted
    ret = []                                #Store the last returned result
    for t,trk in enumerate(trks):      #Loop through the Kalman tracker list
      pos = self.trackers[t].predict()[0]           #Using Kalman tracker t to predict the bbox of the corresponding object in the current frame
      trk[:] = [pos[0], pos[1], pos[2], pos[3], 0]
      if(np.any(np.isnan(pos))):                     #If the predicted bbox is empty, the t-th Kalman tracker will be deleted
        to_del.append(t)
    trks = np.ma.compress_rows(np.ma.masked_invalid(trks))  #Delete the line where the Kalman tracker is predicted to be empty, and finally store the non empty bbox predicted by all objects tracked in the previous frame in the current frame in trks
    for t in reversed(to_del): #to_del array traversal in reverse order
      self.trackers.pop(t)   #Remove to from tracker_ Last frame tracker ID in del
    matched, unmatched_dets, unmatched_trks = associate_detections_to_trackers(dets,trks)  #Associate the incoming detection result with the prediction result of the tracked object in the current frame in the previous frame, return the matched target matrix matched, and unmatched the matrix of the new target_ Dets, leaving the target matrix unmatched_trks
 
    #update matched trackers with assigned detections
    for t,trk in enumerate(self.trackers):    # Traverse the Kalman tracker
      if(t not in unmatched_trks):                   #If t in the previous frame is still in the current frame picture (i.e. not in the matrix unmatched_trks of the current predicted leaving picture)
        d = matched[np.where(matched[:,1]==t)[0],0]  #It shows that the Kalman tracker t is successfully correlated, and the detector d associated with it is found in the matched matrix
        trk.update(dets[d,:][0])                     #Update the Kalman tracker with the associated detection result d (i.e. update the a priori with a posteriori)
 
    #create and initialise new trackers for unmatched detections  #For newly added unmatched detection results, create and initialize the tracker
    for i in unmatched_dets:                  #New target
        trk = KalmanBoxTracker(dets[i,:])     #Pass the newly added unmatched detection results dets[i,:] into Kalman boxtracker
        self.trackers.append(trk)             #Pass the newly created and initialized tracker trk into trackers
    i = len(self.trackers)
    for trk in reversed(self.trackers):       #The new Kalman tracker set is traversed in reverse order
        d = trk.get_state()[0]                #Get the status of trk tracker [x1,y1,x2,y2]       
        if((trk.time_since_update < 1) and (trk.hit_streak >= self.min_hits or self.frame_count <= self.min_hits)):
          ret.append(np.concatenate((d,[trk.id+1])).reshape(1,-1)) # +1 as MOT benchmark requires positive
        i -= 1
        #remove dead tracklet
        if(trk.time_since_update > self.max_age):
          self.trackers.pop(i)
    if(len(ret)>0):
      return np.concatenate(ret)
    return np.empty((0,5))
    
def parse_args():
    """Parse input arguments."""
    parser = argparse.ArgumentParser(description='SORT demo')
    parser.add_argument('--display', dest='display', help='Display online tracker output (slow) [False]',action='store_true')
    args = parser.parse_args()
    return args
 
if __name__ == '__main__':
  # all train
  sequences = ['PETS09-S2L1','TUD-Campus','TUD-Stadtmitte','ETH-Bahnhof','ETH-Sunnyday','ETH-Pedcross2','KITTI-13','KITTI-17','ADL-Rundle-6','ADL-Rundle-8','Venice-2']
  args = parse_args()
  display = args.display
  phase = 'train'
  total_time = 0.0
  total_frames = 0
  colours = np.random.rand(32,3) #used only for display
  if(display):
    if not os.path.exists('mot_benchmark'):
      print('\n\tERROR: mot_benchmark link not found!\n\n    Create a symbolic link to the MOT benchmark\n    (https://motchallenge.net/data/2D_MOT_2015/#download). E.g.:\n\n    $ ln -s /path/to/MOT2015_challenge/2DMOT2015 mot_benchmark\n\n')
      exit()
    plt.ion()  #Used to dynamically draw display images
    fig = plt.figure() 
  
  if not os.path.exists('output'):
    os.makedirs('output')
  
  for seq in sequences:
    mot_tracker = Sort() #create instance of the SORT tracker
    seq_dets = np.loadtxt('data/%s/det.txt'%(seq),delimiter=',') #load detections    #Load test results
    with open('output/%s.txt'%(seq),'w') as out_file:
      print("Processing %s."%(seq))
      for frame in range(int(seq_dets[:,0].max())):   #Determine the total number of frames of the video sequence and perform a for loop
        frame += 1 #detection and frame numbers begin at 1  #Since the frame number of video sequence starts from 1, add 1
        dets = seq_dets[seq_dets[:,0]==frame,2:7]     #Extract [x1,y1,w,h,score] from the test results to dets
        dets[:,2:4] += dets[:,0:2] #convert to [x1,y1,w,h] to [x1,y1,x2,y2] assign the number of columns 2 and 3 in dets plus the number of columns 0 and 1 to columns 2 and 3;
        total_frames += 1          #Cumulative total frames
 
        if(display):        #If results are required
          ax1 = fig.add_subplot(111, aspect='equal')
          fn = 'mot_benchmark/%s/%s/img1/%06d.jpg'%(phase,seq,frame)   #Original image path name
          im =io.imread(fn)      #Load image
          ax1.imshow(im)         #Display image
          plt.title(seq+' Tracked Targets')
 
        start_time = time.time()
        trackers = mot_tracker.update(dets)  #sort tracker update
        cycle_time = time.time() - start_time  #sort tracker time consuming
        total_time += cycle_time               #The sort tracker takes a total of time
 
        for d in trackers:
          print('%d,%d,%.2f,%.2f,%.2f,%.2f,1,-1,-1,-1'%(frame,d[4],d[0],d[1],d[2]-d[0],d[3]-d[1]),file=out_file) #Print: frame,ID,x1,y1,x2,y2,1,-1,-1,-1
          if(display):             #If displayed, draw the target detection box
            d = d.astype(np.int32)
            ax1.add_patch(patches.Rectangle((d[0],d[1]),d[2]-d[0],d[3]-d[1],fill=False,lw=3,ec=colours[d[4]%32,:]))
            ax1.set_adjustable('box-forced')
 
        if(display):
          fig.canvas.flush_events()
          plt.draw()
          ax1.cla()
 
  print("Total Tracking took: %.3f for %d frames or %.1f FPS"%(total_time,total_frames,total_frames/total_time))
  if(display):
    print("Note: to get real runtime results run without the option: --display")

DeepSORT

A year later, the original team released the sequel of SORT, DeepSORT. Up to now, many people are using this tracker.

The overall framework has not been greatly changed, but the idea of Kalman filter plus Hungarian algorithm is continued, and Deep Association Metric is added on this basis. Deep Association Metric is actually a pedestrian identification network learned on a large pedestrian re identification network. The purpose is to distinguish different pedestrians. Personal feeling is very similar to a typical pedestrian recognition network. Output pedestrian pictures, output a set of vectors, and judge whether the two input pictures are the same pedestrian by comparing the distance between the two vectors.

In addition, Appearance Information is added to realize long-term occlusion target tracking.

The tracking process continues. Based on the prediction results of Kalman filter, Hungarian algorithm is used for target allocation, but motion information and appearance information are added in this process. This is simple to say and complex to implement. Interested readers can take a closer look at the paper and code. I won't repeat it here.

There are not many changes in other aspects, but the standard Kalman filter and fixed speed model are used for prediction.

Finally, a better tracking effect is achieved, and it can run in real time (40FPS).

IOU matching flow chart

The author's code also takes the test results as input: bounding box, confidence and feature. conf is mainly used to filter some detection frames; The bounding box and feature (ReID) are used for the match calculation with the tracker; The first is the prediction module, which uses Kalman filter to predict the tracker. The author uses the uniform motion and linear observation model of Kalman filter here (which means that there are only four quantities and the detector will be used for constant value initialization during initialization). The second is the update module, which includes matching, tracker update and feature set update. In the part of updating the module, the fundamental method is to use IOU to match the Hungarian algorithm

1. Use cascade matching algorithm:
Each detector will be assigned a tracker, and each tracker will set a time_since_update parameter. If the tracker completes the match and updates, the parameter will be reset to 0, otherwise it will be + 1. In fact, cascade matching, in other words, is the matching of different priorities. In cascade matching, the tracker will be sorted according to this parameter. Those with small parameters will be matched first, and those with large parameters will be matched later. That is to give high priority to the tracker first matched in the previous frame and lower the priority to the tracker that has not matched in several frames (give up slowly). As for the purpose of using cascade matching:

When a target is occluded for a long time, the uncertainty of kalman filter prediction will greatly increase and the observability in state space will be greatly reduced. If two trackers compete for the matching right of the same detection result at this time, the Mahalanobis distance of the track with longer occlusion time is often smaller, which makes the detection result more likely to be associated with the track with longer occlusion time. This unsatisfactory effect often destroys the continuity of tracking. Let's understand that if the original covariance matrix is a normal distribution, the variance of the normal distribution will become larger and larger if the continuous prediction is not updated. Then the points far from the mean Euclidean distance may obtain the same Mahalanobis distance as the points close to the previous distribution. Therefore, the author uses cascade matching to give priority to more frequent targets. Of course, there are also disadvantages: it may cause some new tracks to be connected to some old tracks. But this situation is rare.

2. Add Mahalanobis distance and cosine distance:
In fact, it is the calculation of motion information and appearance information. The two nouns sound strange, but in fact, in other words, Mahalanobis distance is "enhanced Euclidean distance". In fact, it avoids the risk of different variance of data characteristics in Euclidean distance, and adds covariance matrix in the calculation. Its purpose is to normalize the variance, so as to make the so-called "distance" more in line with the data characteristics and practical significance. Mahalanobis distance is a distance measurement method in the measurement of difference, while different from Mahalanobis distance, cosine distance is a similarity measurement method. The former is aimed at the position, while the latter is aimed at the direction. In other words, when we use cosine distance, it can be used to measure the differences between dimensions of different individuals, but it is difficult for us to judge the differences between dimensions in an individual. At this time, we can use Mahalanobis distance to make up for it, so as to achieve a comprehensive difference measurement on the whole. The fundamental reason why we want to measure the difference is to compare the similarity between the detector and the tracker, optimize the measurement method, and better complete the matching.

3. Add deep learning features:
This part is the module of ReID and one of the highlights of deepsort. Deepsort adds a deep learning Feature extraction network to the improvement of sort. In the part of network structure, you can step by step. The author stores the feature map of the corresponding detection in a list after all confirmed trackers (one of the States) complete matching each time. The author uses the budget super parameter (100 frames) to limit the amount of storage (i think if the real-time effect is not good, you can lower this parameter to speed up the speed). Therefore, after each matching, we will update the list of this feature map, such as removing some Feature sets of targets that have been shot, retaining the latest features, and pop ping out the old features. This Feature set will play a role in the calculation of cosine distance. In fact, in the current frame, the minimum cosine distance between all Feature vectors tracked by the ith object and the detection of the jth object will be calculated.

4. Matching between IOU and Hungarian algorithm:
This method is proposed in sort. It's a relatively strange noun again. I then "in other words". In fact, the Hungarian algorithm can be understood as an idea of "as many as possible". For example, detector a can match with trackers A and c (the configuration reliability of matching with a is higher), but detector B can only match with tracker a. In the algorithm, a and c will complete the matching, and B and a will complete the matching, so as to reduce the consideration of confidence. Therefore, the fundamental purpose of the algorithm is not to match accurately, but to match as much as possible, which is the fundamental purpose of the author to add cascade matching, Markov distance and cosine distance in deepsort, because only using Hungarian algorithm for matching is particularly easy to cause ID switch, that is, a detection frame id is constantly replaced, Lack of accuracy and robustness. What is the high confidence of matching? In fact, here, the author uses IOU to measure, calculate the IOU of detector and tracker, and take this as the level of confidence (relatively rough).

There are also some super parameters, which I have clearly explained in the part of code flow. These super parameters either perform the function of threshold or limit the number of cycles, and constantly help the algorithm complete the optimal matching and tracker update. After that, delete the unmatched tracker, initialize the unmatched detector, assign the value of the matched tracker with the corresponding detector as the output, and enter the next cycle.

Interpretation of Deepsort code
Another excellent interpretation of Deepsort principle: https://blog.csdn.net/sgfmby1994/article/details/98517210

Original link: https://blog.csdn.net/qq_46098574/article/details/115875336