1. Bubble sorting

Bubble sorting principle:

1) Compare two adjacent elements. If the preceding element is larger than the following element, exchange the two numbers. After the first traversal, the maximum number will be placed at the last position of the array, that is, array[length - 1].
2) The last element is skipped during the second traversal because it has been determined to be the maximum value by the first traversal.
3) Continue to repeat the above steps for fewer and fewer elements at a time until no pair of numbers need to be compared.

Code implementation:

import java.util.Arrays;

/**
 * Bubble sorting
 * Principle: compare adjacent elements. If the first is bigger than the second, swap their positions.
 */
public class BubbleSortDemo {
    public static void sort(int arr[]) {
        int temp = 0;
        //External circulation, it decides how many times to go
        for (int i = 0; i < arr.length - 1; i++) {
            //Unnecessary comparison can be reduced through the sign bit. If it has been ordered, it will exit the loop
            int flag = 0;
            //Internal circulation, it decides to go several times at a time
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    flag = 1;
                }
            }
            if (flag == 0) {
                break;
            }
        }
        System.out.println(Arrays.toString(arr));
    }

    public static void main(String[] args) {
        int[] arr = new int[]{12, 34, 21, 54, 43, 21, 53};
        BubbleSortDemo.sort(arr);
    }
}

2. Insert sort

Insert sort principle:

Assuming that the first element has been sorted, compare it forward from the second element, find the corresponding position and insert it.

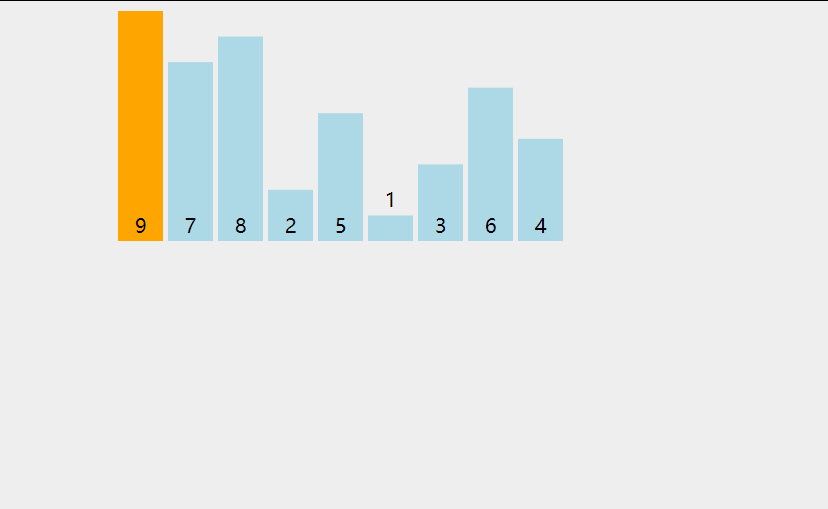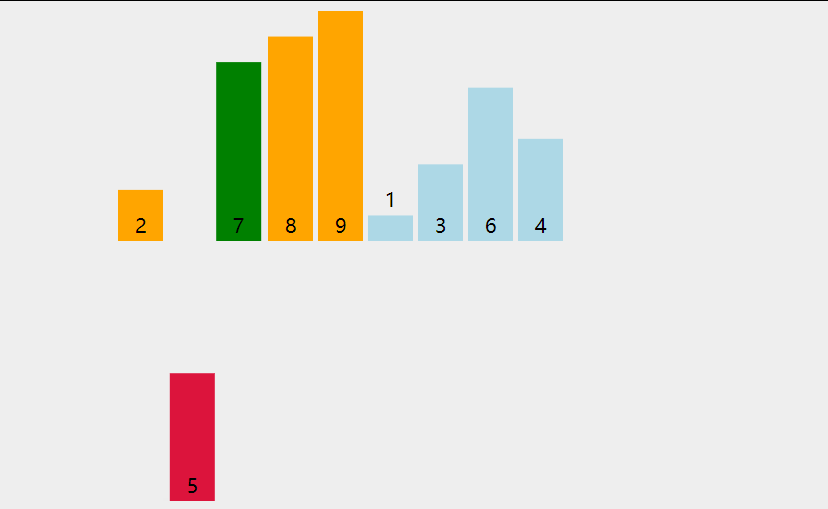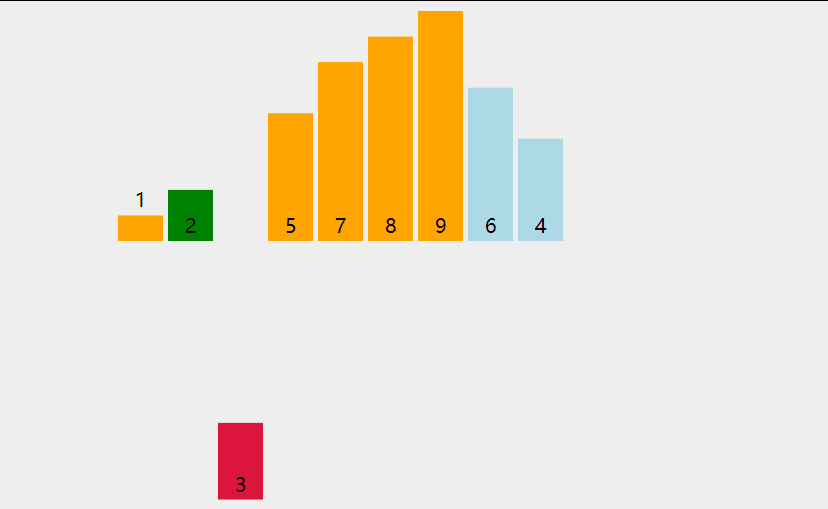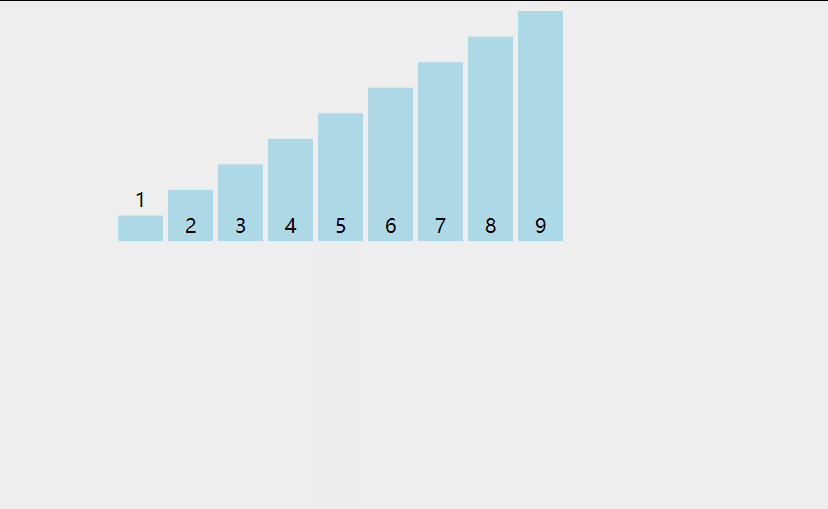
Code implementation:

import java.util.Arrays;

/**
 * Insert sort
 * Principle: by constructing an ordered sequence, for unordered data, scan from back to front in the sorted sequence, find the corresponding position and insert it.
 */
public class InsertSortDemo {
    public static void sort(int arr[]) {
        int i, j;
        //Outer loop, assuming that the first element has been sorted, and i is the subscript of the second element
        for (i = 1; i < arr.length; i++) {
            //Assign the second element to the temporary variable temp
            int temp = arr[i];
            //Inner loop: if the second element is smaller than the previous element, the second element moves forward one bit, j-- to continue the forward comparison
            for (j = i; j > 0 && temp < arr[j - 1]; j--) {
                arr[j] = arr[j - 1];
            }
            arr[j] = temp;
        }
        System.out.println(Arrays.toString(arr));
    }

    public static void main(String[] args) {
        int[] arr = new int[]{12, 34, 21, 54, 43, 21, 53};
        InsertSortDemo.sort(arr);
    }
}

3. Select Sorting

Select sorting principle:

Each time, the smallest element is selected from the data elements to be sorted and stored at the beginning of the sequence until all the data elements to be sorted are finished.

Code implementation:

import java.util.Arrays;

/**
 *  Select sort
 *  Principle: select the smallest (or largest) element from the data elements to be sorted each time and store it at the beginning of the sequence until all the data elements to be sorted are finished.
 */
public class SelectSortDemo {
    public  static void sort(int arr[]){
        int temp = 0;
        for(int i=0; i<arr.length-1; i++){
            //Think that the current number is the smallest, and record the subscript of the smallest number
            int minIndex = i;
            for(int j=i+1; j<arr.length; j++){
                if(arr[minIndex]>arr[j]){
                    //Modify the subscript of the minimum value
                    minIndex = j;
                }
            }
            //When you exit the for loop, you find the minimum value this time
            if (i != minIndex){
                temp = arr[i];
                arr[i] = arr[minIndex];
                arr[minIndex] = temp;
            }
        }
        System.out.println(Arrays.toString(arr));
    }
    
    public static void main(String[] args) {
        int[] a = new int[]{23,14,43,45,67,2,22,15,32};
        SelectSortDemo.sort(a);
    }
}

4. Quick sort

Quick sort principle:

1) Take a number from the data to be sorted as "benchmark number".
2) The data to be sorted is divided into two independent parts through one-time sorting. The data on the left is smaller than the "benchmark number" and the data on the right is larger than the "benchmark number".
3) Then quickly sort the two parts of data according to step 2. The whole sorting process can be recursive, so that the whole data becomes an ordered sequence.

Code implementation:

/**
 * Quick sort
 * 1)Take a number from the data to be sorted as "benchmark number".
 * 2)The data to be sorted is divided into two independent parts through one-time sorting. The data on the left is smaller than the "benchmark number" and the data on the right is larger than the "benchmark number".
 * 3)Then quickly sort the two parts of data according to step 2. The whole sorting process can be recursive, so that the whole data becomes an ordered sequence.
 */
public class TestQuickSort {
    private static void quickSort(int[] array, int low, int high) {
        if (low >= high) {
            return;
        }
        int i = low, j = high, index = array[i]; // Take the leftmost number as the benchmark
        while (i < j) {
            while (i < j && array[j] >= index) { // Find the first number less than index to the left
                j--;
            }
            if (i < j) {
                array[i++] = array[j]; // Fill array[j] into array[i] and move I to the right
            }
            while (i < j && array[i] < index) {// Look to the right for the first number greater than index
                i++;
            }
            if (i < j) {
                array[j--] = array[i]; // Fill array[i] into array[j] and move j to the left
            }
        }
        array[i] = index; // Fill the base number into the last pit
        quickSort(array, low, i - 1); // Recursive call, divide and conquer
        quickSort(array, i + 1, high); // Recursive call, divide and conquer
    }

    public static void sort(int[] array) {
        if (array == null || array.length == 0) {
            return;
        }
        quickSort(array, 0, array.length - 1);
    }

    public static void main(String[] args) {
        int[] a = new int[]{23,14,43,45,67,2,22,15,32};
        TestQuickSort.sort(a);
    }
}

5. Binary search algorithm

Binary search algorithm

• Defect of binary search algorithm: forced dependence on ordered array.
• The defect of array is that there is no way to insert quickly and expand capacity.
• Therefore, we can use binary search tree to improve performance and have the same flexibility as linked list.
• For example, the efficiency of binary tree search is very low.

This leads to the AVL balance tree:

• 1.AVL number has all the characteristics of binary tree;
• 2. The height difference between the number of left and right subtrees of each node is at most 1.

Code implementation:

public class BinarySearchDemo {
    public static void main(String[] args) {
        int[] arr = new int[]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
        System.out.println(binarySearch(arr, 6));
    }

    /**
     * @param arr  Ordered array
     * @param data Find data
     * @return index Subscript, return - 1 when searching
     */
    public static int binarySearch(int[] arr, int data) {
        int low = 0;
        int height = arr.length - 1;

        while (low <= height) {
            int mid = low + (height - low) / 2;

            if (arr[mid] < data) {
                low = mid + 1;
            } else if (arr[mid] == data) {
                return mid;
            } else {
                height = mid - 1;
            }
        }
        return -1;
    }
}