Quick sort is an exchange sort method of binary tree structure proposed by Hoare in 1962. Its basic idea is: any element in the element sequence to be sorted is taken as the reference value, and the set to be sorted is divided into two subsequences according to the sort code. All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value, Then repeat the process for the leftmost and leftmost subsequences until all elements are arranged in corresponding positions.

There are three main methods of fast platoon

1.hoare version

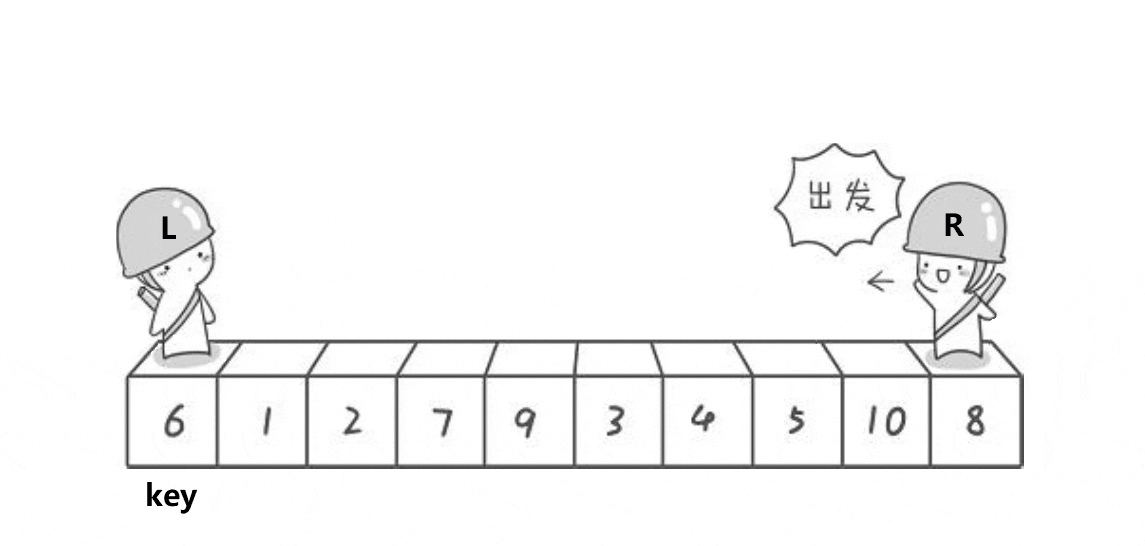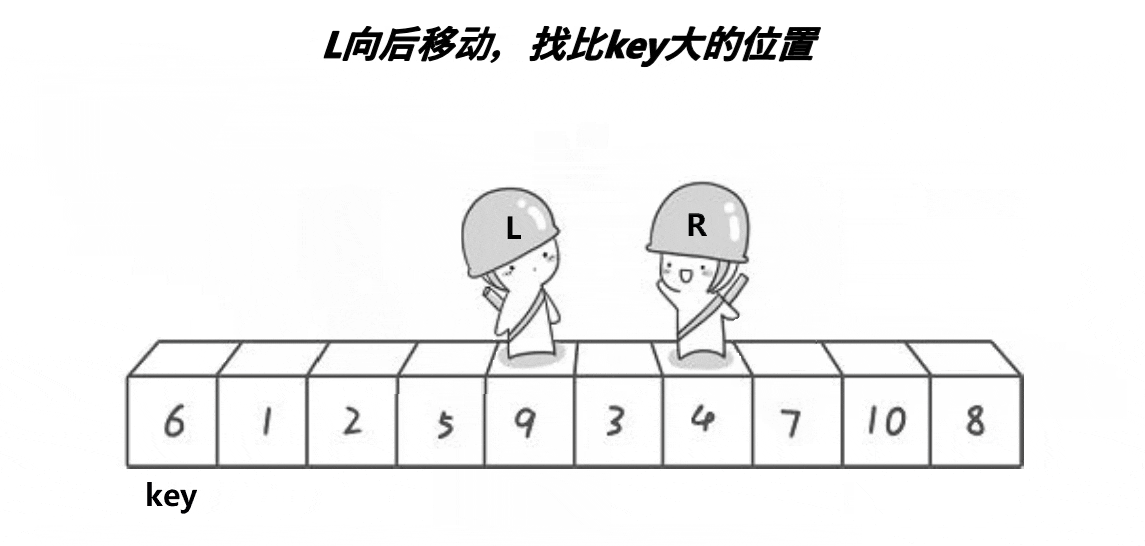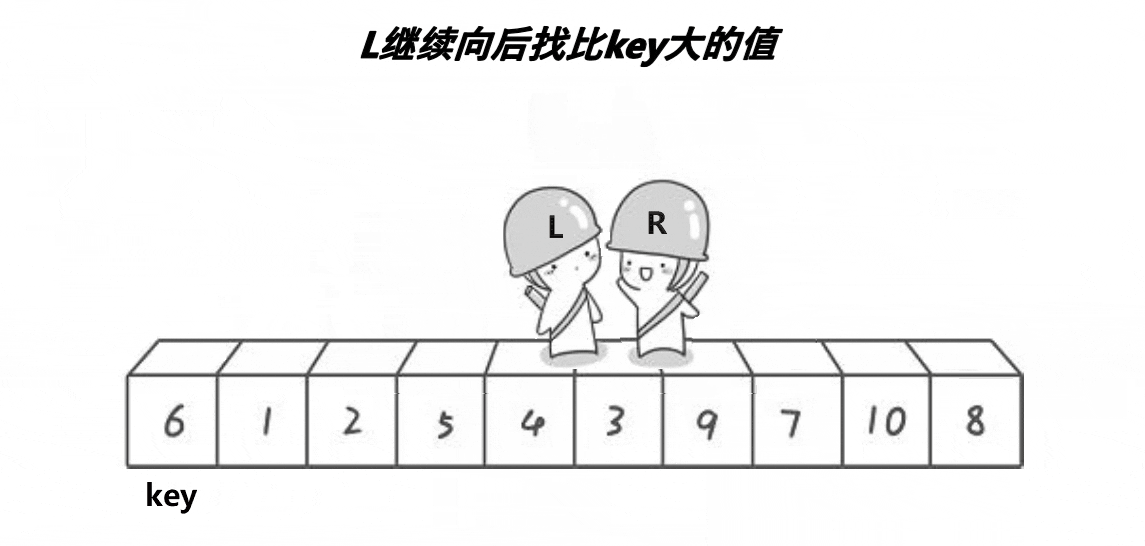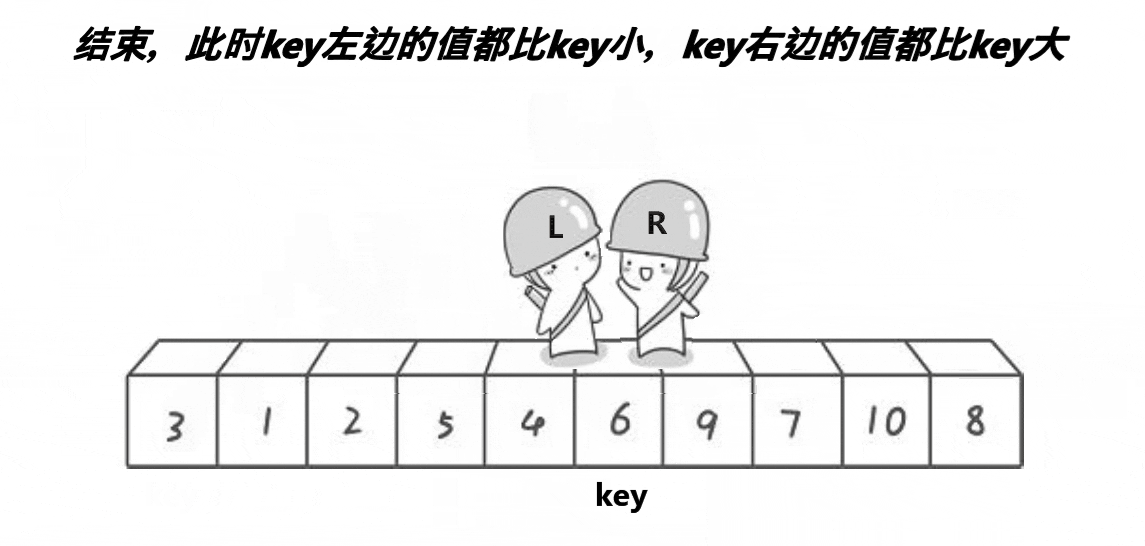
Select the leftmost number as the reference object key, the pointer left points to the first number on the left (subscript 0), and the pointer right points to the first number on the right (subscript n-1). Go first on the right, stop when it is smaller than the key, go left again, stop when it is larger than the key, exchange the positions of left and right, and continue the above process until left and right meet, and exchange the key with the place where they meet.

Select the rightmost number as the reference object key, then go first on the left, stop when it is large, go again on the right, and stop when it is small. This exchange and cycle this process until they meet, and exchange the key and the meeting point.

The above is a sequence. The first sequence is smaller than the key on the left and larger than the key on the right. Then continue to sort the left and right of the key as new unordered sequences, and their range becomes: [0,key-1],[key+1,N-1] to find the new key. Until the subscript of left is greater than or equal to the subscript of right.

 

void Swap(int* px, int* py)
{
	int tmp = *px;
	*px = *py;
	*py = tmp;
}
//hoare version
int Partion1(int* a, int left, int right)
{
	//Middle of three numbers -- in the face of the ordered worst case, let the median be the key and become the best case
	int midi = GetMidIndex(a, left, right);
	Swap(&a[left], &a[midi]);

	//key is on the left
	int keyi = left;
	while (left < right)
	{
		//Go first on the right and find the small one
		while (left < right&&a[right] >= a[keyi])
			--right;

		while (left < right && a[left] <= a[keyi])
			++left;
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	return left;
}
void QSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = Partion1(a, left, right);
	QSort(a, left, keyi - 1);
	QSort(a, keyi + 1, right);
}

[summary]:

• Select the leftmost value as the key, and go first on the right -- > when the left and right meet, it is smaller than the key
• Select the value on the far right as the key, and go first on the left -- > when the left meets the right, it is larger than the key

After a single trip, those smaller than the key are placed on the left and those larger than the key are on the right. If the left sub interval is good and the right sub interval is orderly, the whole will be orderly.

It is found that the key value arranged each time is in the middle. It is assumed that the key selected each time is the median

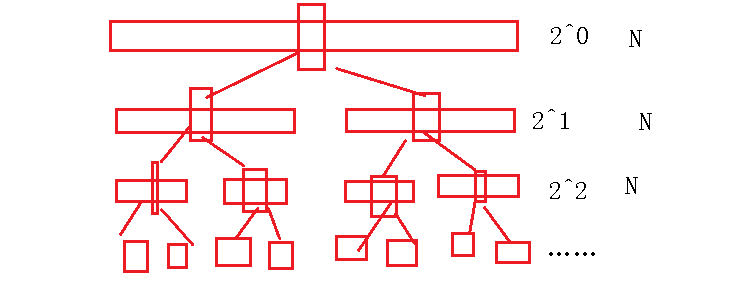
[best]: Calculation of height: for each walk of 2^n, X numbers shall be calculated in total. It is calculated by the sum of the equal ratio sequence: 2^n = x, N = logn (logarithm of N with 2 as the base)

N numbers are arranged every time, so the time complexity is O(N*logN)

[worst]: the ordered array is traversed from the first number. If the leftmost value is the key value, it is traversed from the right. The values on the right are larger than the key. It has traversed N times, and the time complexity is O(N^2)

This is a defect of fast array. When arranging an ordered array, the time complexity is very large.

Therefore, in order to solve this problem, we take the middle of three numbers, left, mid and right, and take the middle number as the key value

int GetMidIndex(int* a, int left, int right)
{
	//int mid = (left + right) / 2;
	int mid = left + ((right - left) >> 1);
	if (a[left] < a[mid])
	{
		if (a[right]<a[left])
		{
			return left;
		}
		else if (a[mid] < a[right])
		{
			return mid;
		}
		else
		{
			return right;
		}
	}
	else//a[left]>=a[mid]
	{
		if (a[right] > a[left])
		{
			return left;
		}
		else if (a[mid] > a[right])
		{
			return mid;
		}
		else
		{
			return right;
		}
	}
}

int Partion1(int* a, int left, int right)
{
	//Middle of three numbers -- in the face of the ordered worst case, let the median be the key and become the best case
	int midi = GetMidIndex(a, left, right);
	Swap(&a[left], &a[midi]);
    
    //...
}

2. Excavation method

Select the leftmost key value and turn it into a pit position. Left is the leftmost subscript and right is the rightmost subscript. On the left is the pit. Start from the right, find the small one on the right, find it and put it into the pit on the left. Update the subscript of right to the pit. Then go to the left, find the big one on the left, find it and put it in the pit on the right. Update the found left value subscript to the pit, and repeat this process until they meet. Put the value of key into the pit and return to the pit subscript.

In this way, the values on the left are smaller than those of the key in the pit, and the values on the right are larger than those of the key in the pit. Repeat the above process in the left and right areas.

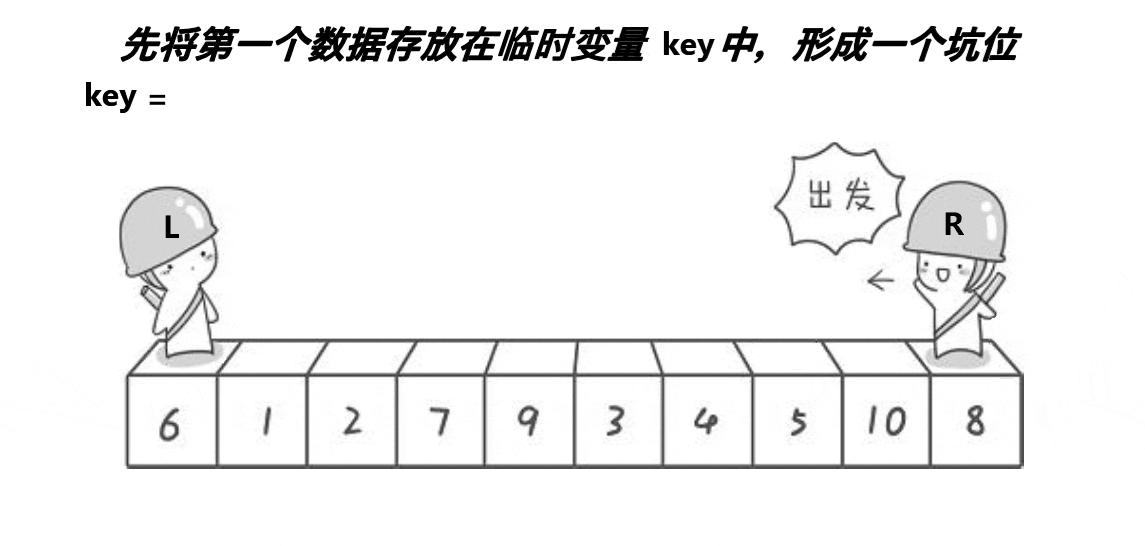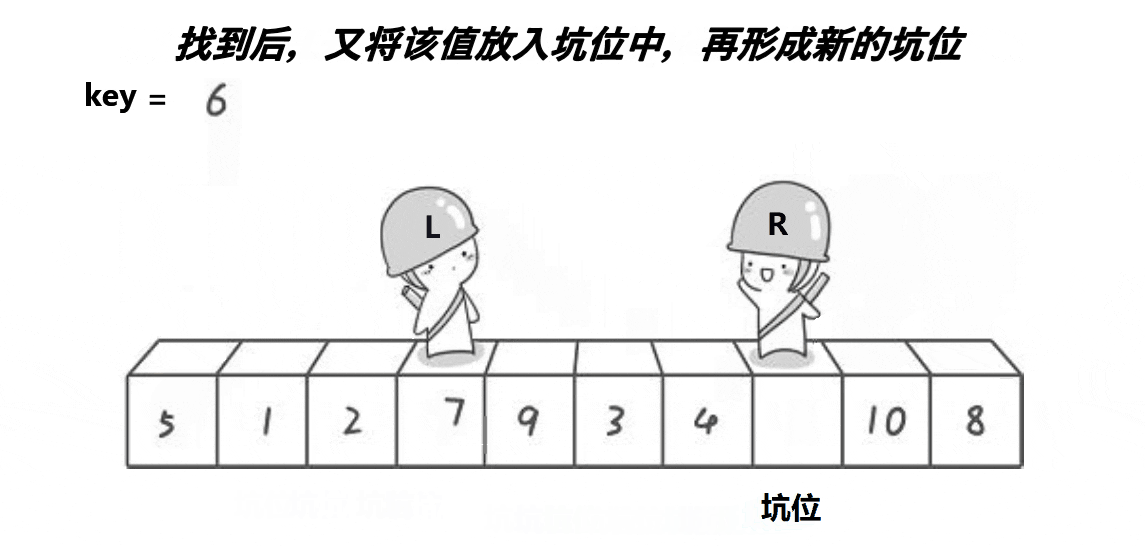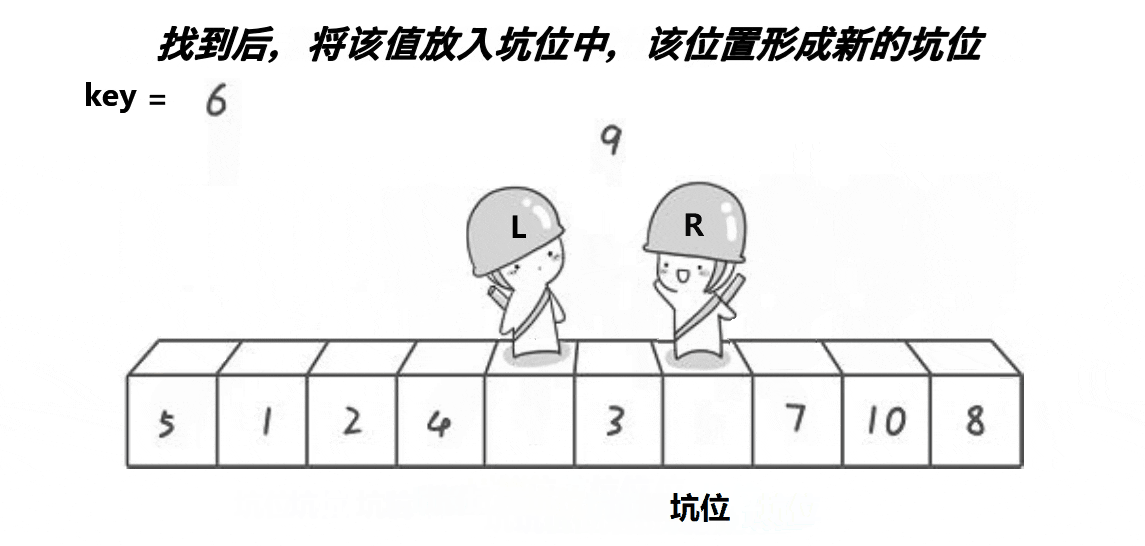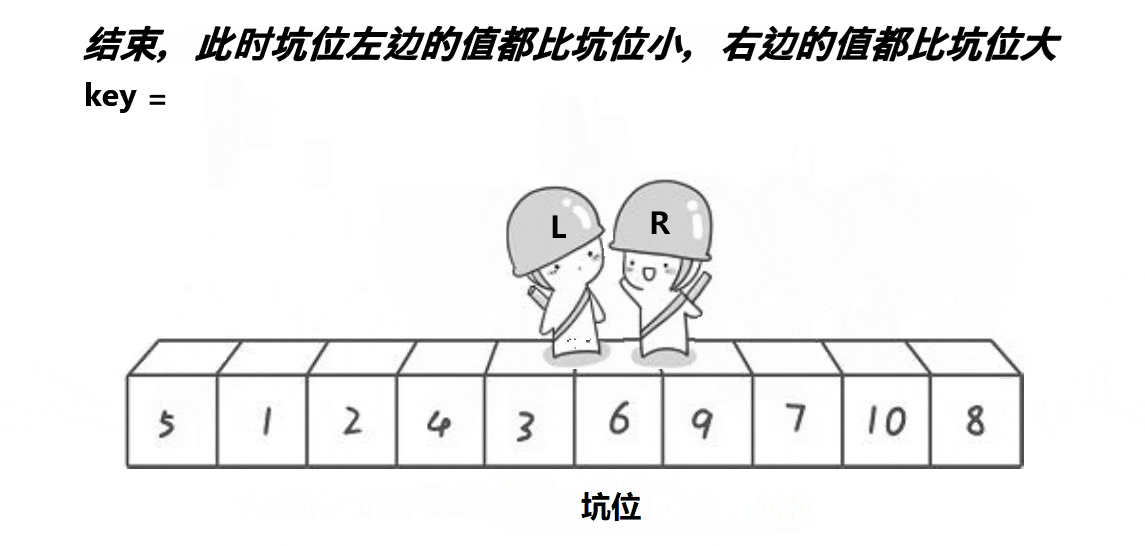
//Excavation method
int Partion2(int* a, int left, int right)
{
	int mid = GetMidIndex(a, left, right);
	Swap(&a[mid], &a[left]);

	int pivot = left;
	int keyi = left;
	//Start from the right, meet a small pit and update the pit
	while (left < right)
	{
		while (left < right&&a[right] >= a[keyi])
		{
			right--;
		}
		a[pivot] = a[right];
		pivot = right;

		//Go to the left and meet a large pit. Update the pit
		while (left < right&&a[left] <= a[keyi])
		{
			left++;
		}
		a[pivot] = a[left];
		pivot = left;
	}
	//When they meet, they jump out of the cycle and put the key into the pit
	a[pivot] = a[keyi];
	return pivot;
}
void QSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = Partion2(a, left, right);
	QSort(a, left, keyi - 1);
	QSort(a, keyi + 1, right);
}

3. Front and rear pointer versions

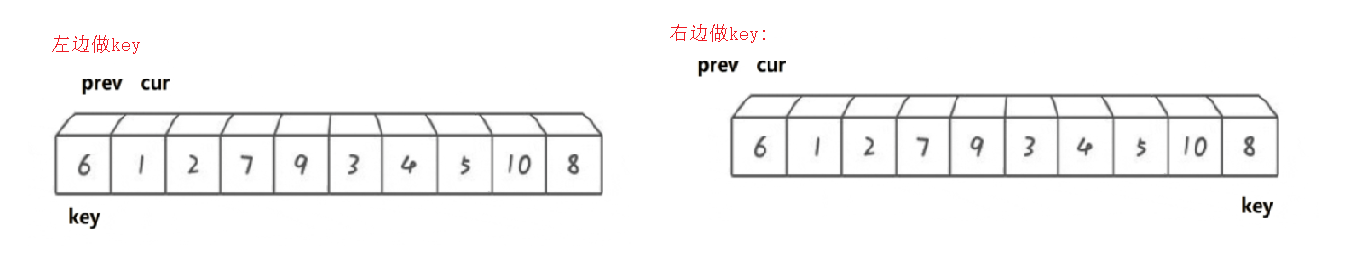
You can select the left as the key or the right as the key

Key on the left: two pointers prev and cur are used here. When the value in cur is smaller than the key, cur and prev + + exchange. If the value of cur is greater than or equal to the key, continue to look down., Until cur traverses the entire array. Exchange the value of key with prev.

Make key on the right: when making key on the right, cur still points to the previous key and prev points to the latter cur. As in the above procedure, when cur is greater than or equal to the value of key, look down, find the value smaller than key, prev + + and exchange with cur. But at this time, when cur traverses the entire array, prev needs to use + + again, and then exchange with key.

 

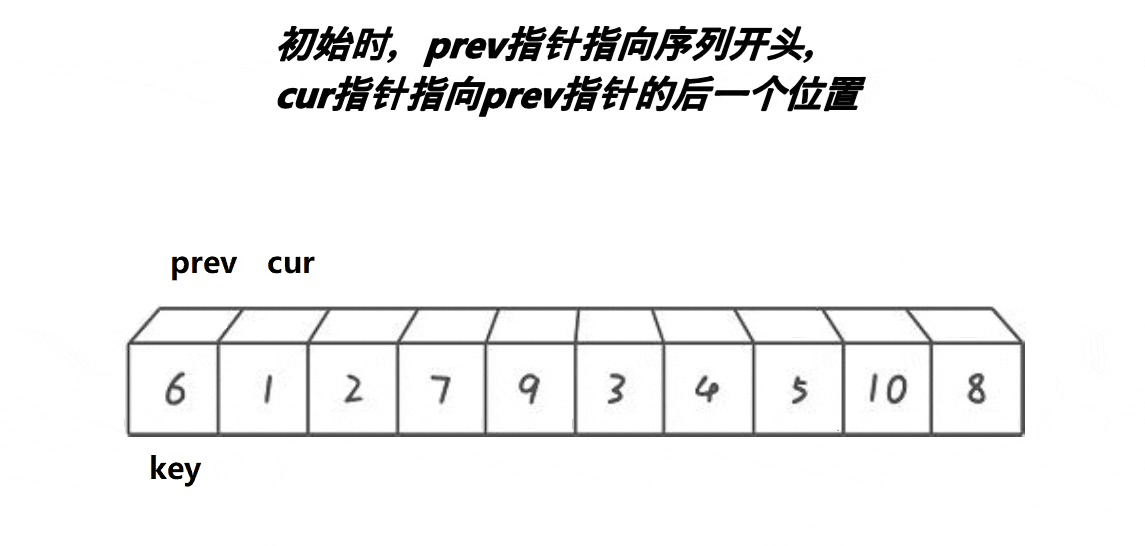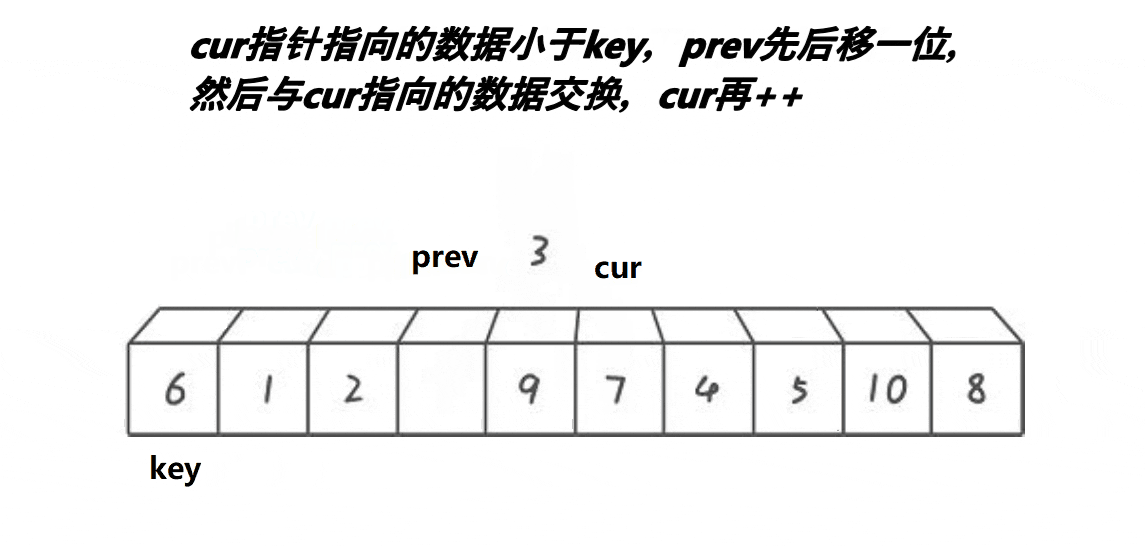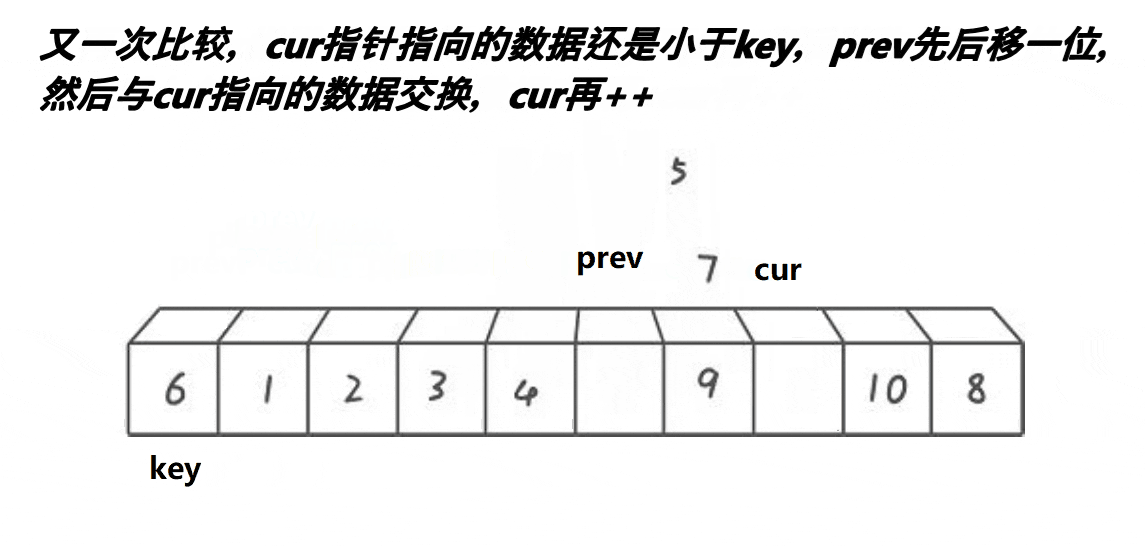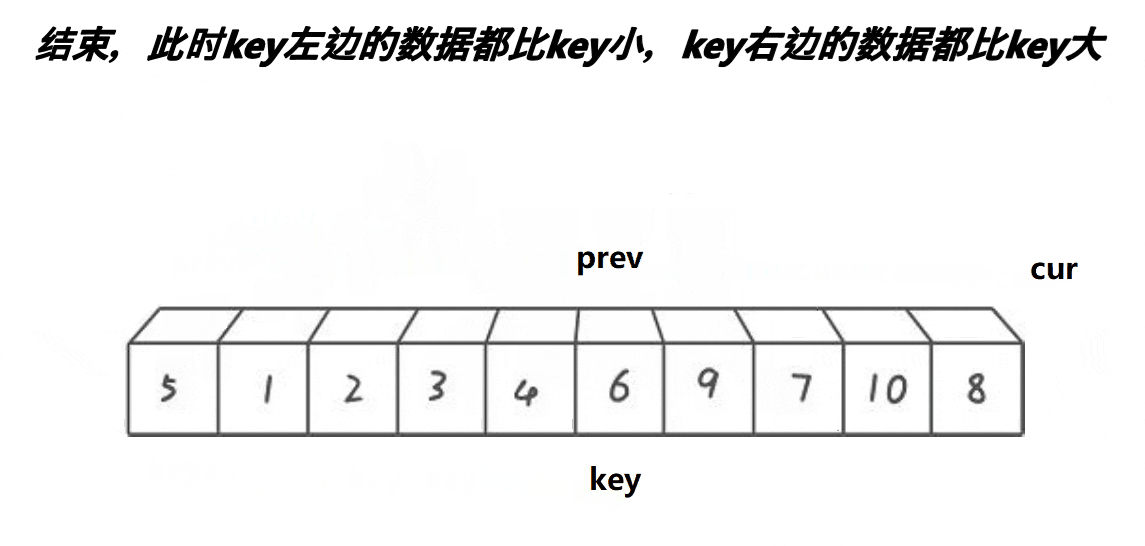
int Partion3(int* a, int left, int right)
{
	int keyi = left;
	int prev = left;
	int cur = left + 1;
	//When cur is smaller than key, exchange prev + + and cur and find the smaller one
	while (cur <= right)
	{
		while (cur<=right && a[cur] >= a[keyi])
		{
			++cur;
		}
		if (cur > right)
			break;
		++prev;
		if (prev == cur)
		{
			cur++;
		}
		else
		{
			Swap(&a[prev], &a[cur]);
			++cur;
		}
	}
	Swap(&a[prev], &a[keyi]);
	return prev;

	//int keyi = left;
	//int prev = left;
	//int cur = left + 1;
	//while (cur <= right)
	//{
	//	if (a[cur] < a[keyi] )//&& ++prev != cur)
	//	{
	//		++prev;
	//		Swap(&a[cur], &a[prev]);
	//	}
	//	++cur;
	//}
	//Swap(&a[prev], &a[keyi]);
	//return prev;
}
void QSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = Partion3(a, left, right);
	QSort(a, left, keyi - 1);
	QSort(a, keyi + 1, right);
}

4. Non recursive algorithm

[defects of recursive program]:

1. For early compilers, the performance of recursion is worse than that of circular programs, because the optimization of establishing stack frame is not large for recursive calls. Now the compiler optimization is very good, and the performance of recursion is not much worse than that of loop

2. Too deep recursion will lead to stack overflow, which is why we use the method of three data fetching.

The non recursive method is applied to the stack, because it is necessary to get the range of the array, and put the first number and the last number of the array into the stack in turn. Because the nature of the stack is first in and last out, the number at the top of the stack is the last number of the array. Delete it, and then get the first number of the array. If you get two numbers, get the subscripts of them and sort them, Then put the left and right subscripts of the new array into the stack, get their subscripts again and sort them until the left subscript is not less than the right subscript, and the cycle stops.

It is equivalent to using medium order traversal

//non-recursive 
void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	StackInit(&st);
	StackPush(&st, left);
	StackPush(&st, right);

	while (!StackEmpty(&st))
	{
		int end = StackTop(&st);
		StackPop(&st);

		int begin = StackTop(&st);
		StackPop(&st);

		int keyi = Partion3(a, begin, end);
		//[begin,keyi-1] keyi [keyi+1,end];
		if (begin < keyi - 1)
		{
			StackPush(&st, begin);
			StackPush(&st, keyi - 1);
		}
		if (keyi + 1 < end)
		{
			StackPush(&st, keyi + 1);
			StackPush(&st, end);
		}
	}
    //malloc's space needs to be released
	StackDestroy(&st);
}

Implementation of stack