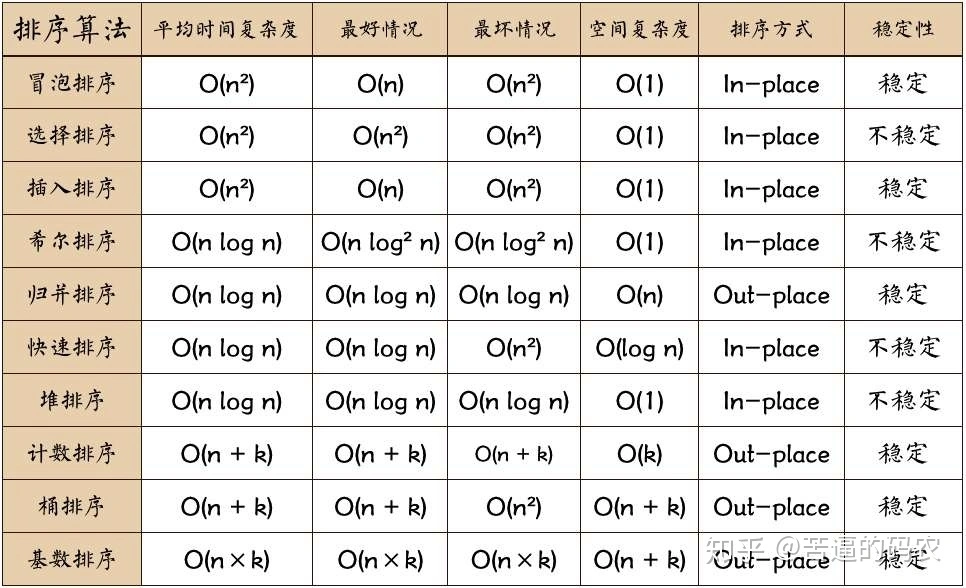
1 Classification of sorting algorithms
1.1 stable sorting vs unstable sorting
- Stable sorting: for elements with the same value, the relative positions before and after sequence sorting remain the same, that is, if Ai = Aj, Ai is before Aj, and Ai is still before Aj after sorting. Such as insert sort, bubble sort and merge sort.
- Unstable sorting: the relative positions of elements with the same value before and after sequence sorting may not be consistent, such as selective sorting, fast sorting and heap sorting.
- Note: for elements with different values, the effect of stable sorting and unstable sorting is the same.
1.2 internal sorting VS external sorting
- Internal sorting: read the data to be sorted into memory at one time for sorting;
- External sorting: when the data to be sorted is very large, that is, the data cannot be read into memory at one time. It is necessary to sort the data with the help of external memory and memory.
2 select sort
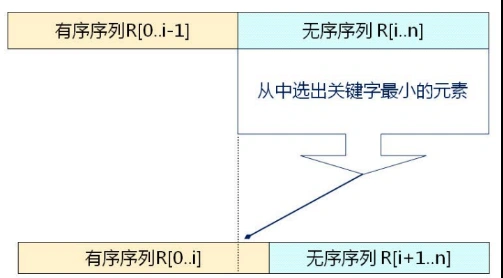
2.1 ideas
- Each time (for example, the ith time, i=0, 1, 2,..., n-2), select the element with the smallest keyword from the following n-i data elements to be sorted as the ith element of the ordered element sequence.
- Example of the i-th sorting:
2.2 code implementation
void select_sort(int *num, int n) {
for (int i = 0; i < n - 1; i++) {
int ind = i; // Index of minimum value
for (int j = i + 1; j < n; j++) {
if (num[j] < num[ind]) ind = j;
}
// ind != i indicates that a new minimum element index was found
if (ind != i) swap(num[i], num[ind]);
}
return ;
}
3 insert sort
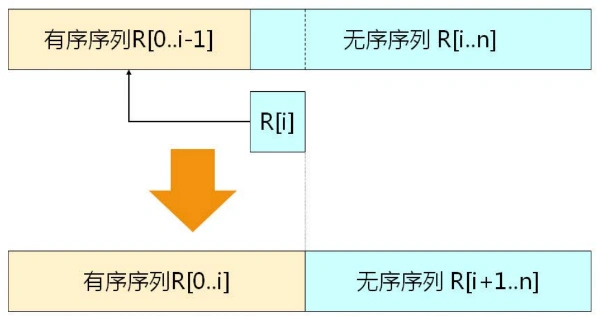
3.1 ideas
- When the i (i ≥ 1) th data element is inserted, the previous V[0], V[1], V[i-1] has been arranged; At this time, use the keyword of V[i] and V[i-1], V[i-2], Compare the keywords of V[0], insert V[i] after finding the position, and move the object in the original position backward.
- Example of inserting the ith element:
3.2 code implementation
void insert_sort(int *arr, int len) {
for (int i = 1; i < len; i++) {
int k = i;
int v = arr[i];
for (int j = i - 1; (j >= 0) && (v < arr[j]); j--) {
arr[j + 1] = arr[j];
k = j;
}
if (k != i) arr[k] = v;
}
return ;
}
4 bubble sorting
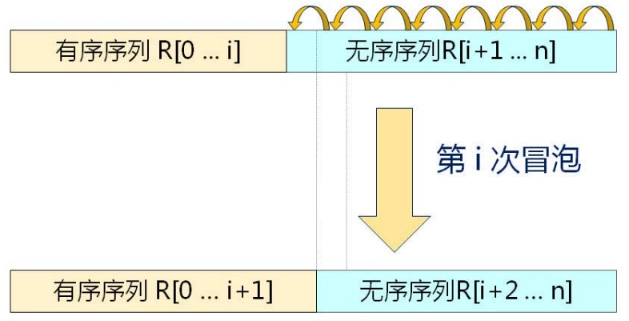
4.1 ideas
- Each time from back to front (assuming the i-th time), j=n-1, n-2, i. Compare the keywords of V[j-1] and V[j] in pairs; If reverse order occurs, exchange V[j-1] and V[j];
- Note: in the bubble sorting algorithm, if there is no element exchange operation in a bubble process, it indicates that the sequence at this time is an ordered sequence and should be ended in advance; (optimization means)
- Example of the ith bubbling:
4.2 code implementation
void bubble_sort(int* arr, int len) {
int exchange = 1;
for (int i = 0; (i < len) && exchange; i++) {
exchange = 0;
for (int j = len - 1; j > i; j--) {
if (arr[j] < arr[j - 1]) {
swap(arr[j], arr[j - 1]);
exchange = 1;
}
}
}
return ;
}
5 Hill sort
5.1 ideas
- Divide the sequence to be sorted into several groups, insert sort in each group to make the whole sequence basically orderly, and then insert sort the whole sequence;
5.2 code implementation
void Shell(int* arr, int len) {
int d = len;
do {
d = d / 3 + 1;
for (int i = d; i < len; i += d) {
int k = i;
int v = arr[i];
for (int j = i - d; (j >= 0) && (v < arr[j]); j -= d) {
arr[j + d] = arr[j];
k = j;
}
if (k != i) arr[k] = v;
}
} while (d > 1);
return ;
}
6 merge sort
6.1 ideas
- Merge two ordered sequences into a new ordered sequence. This merging method is called 2-way merging, and its time complexity is \ (O(n*log_2n) \);

- Merging routine:
- Merging three ordered sequences into a new ordered sequence is called 3-way merging;
- Merging N ordered sequences into a new ordered sequence is called N-way merging;
- Merging multiple ordered sequences into a new ordered sequence is called multi-channel merging;
- Example display of 2-way merging:

-
Question: how to sort 20G data on a computer with 4G memory?
A: divide 20G data into 10*2G, sort each 2G data separately, and then merge them;
6.2 code implementation
void merge_sort(int* arr, int l, int r) {
if (r == l) return; // Recursive exit
// Two way merging
int mid = l + (r - l) / 2;
merge_sort(arr, l, mid);
merge_sort(arr, mid + 1, r);
// Merge left and right arrays - > copy
int* temp = (int*)malloc(sizeof(int) * (r - l + 1));
int p1 = l, p2 = mid + 1, p = 0; // p1: the subscript of the first element of data on the left, p2: the subscript of the first element of data on the right
while (p1 <= mid || p2 <= r) {
// P2 > R: the right array element traversal ends
if (p2 > r || (p1 <= mid && arr[p1] <= arr[p2])) {
temp[p++] = arr[p1++];
} else {
temp[p++] = arr[p2++];
}
}
memcpy(arr + l, temp, sizeof(int) * (r - l + 1));
free(temp);
return ;
}
7 quick sort
7.1 ideas
- Taking any element in the sequence as the benchmark, the whole sequence is divided into left and right subsequences;
- All elements in the left subsequence are less than or equal to the reference element, and all elements in the right subsequence are greater than the reference element; (sort in ascending order)
- The reference element is arranged in the middle of the two subsequences;
- The two subsequences are divided repeatedly until all the data elements are arranged in the corresponding positions; (recursive implementation)
- Example of fast platoon:
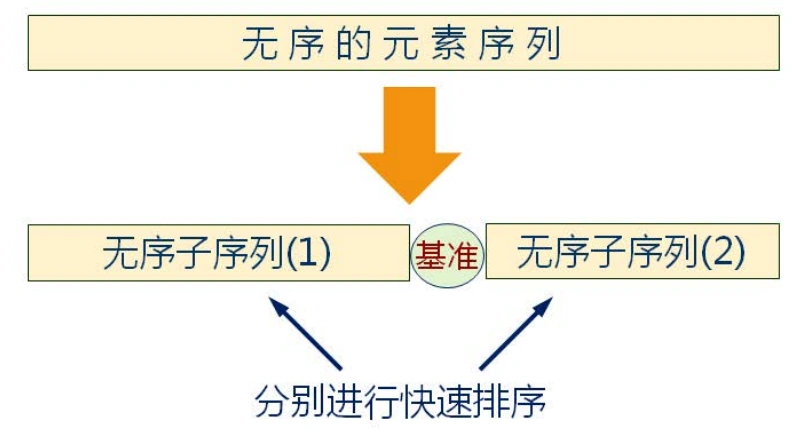
7.2 code implementation
void quick_sort(int *num, int l, int r) {
if (l >= r) return ;
int x = l, y = r, z = num[x]; // x: Position of head pointer; y: Position of tail pointer; z: Primary element, which defaults to the first element of the array to be sorted
while (x < y) {
while (x < y && num[y] > z) y--;
if (x < y) num[x++] = num[y];
while (x < y && num[x] < z) x++;
if (x < y) num[y--] = num[x];
}
num[x] = z;
quick_sort(num, l, x - 1);
quick_sort(num, x + 1, r);
return ;
}
8 sorting algorithm induction