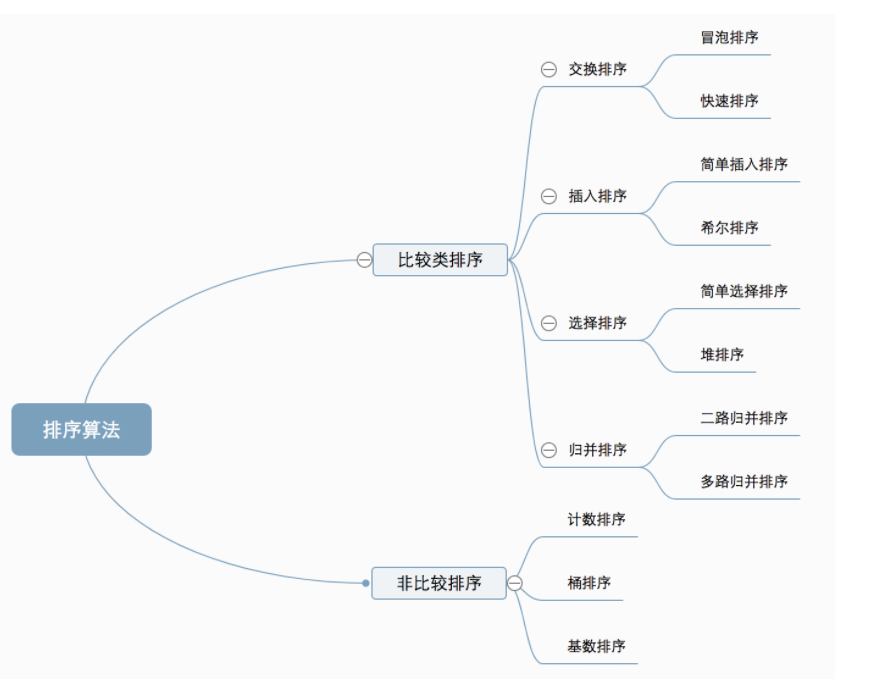
classification
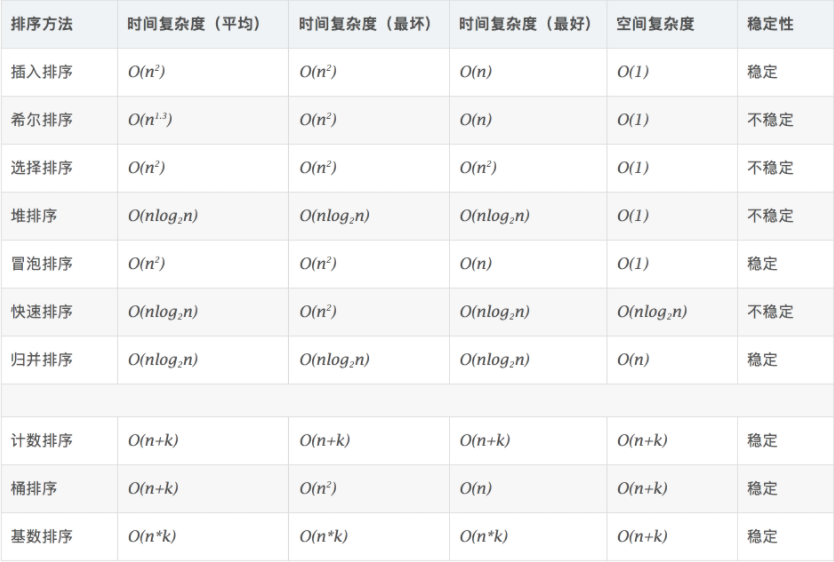
How to judge whether the sorting is stable
Stable: if a is in front of b and a=b, a is still in front of b after sorting.
Unstable: if a was originally in front of b and a=b, a may appear after b after sorting.
1. Bubble sorting
Algorithm process:
Compare adjacent elements. If the first one is bigger than the second, exchange them two;
Do the same work for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end, so that the last element should be the largest number;
Repeat the above steps for all elements except the last one;
Repeat steps 1 to 3 until the sorting is completed.
Implementation code:
function bubbleSort(arr) {
var len = arr.length;
for (var i = 0; i < len - 1; i++) {
for (var j = 0; j < len - 1 - i; j++) {
if (arr[j] > arr[j+1]) {//Pairwise comparison of adjacent elements
var temp = arr[j+1];// Element exchange
arr[j+1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
2. Selection sort
A simple and intuitive sorting algorithm. Its working principle: first, find the smallest (large) element in the unordered sequence and store it at the beginning of the sorted sequence, then continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence. And so on until all elements are sorted.
Algorithm description:
The direct selection sorting of n records can get ordered results through n-1 times of direct selection sorting. The specific algorithm is described as follows:
Initial state: the disordered area is R[1... n], and the ordered area is empty;
At the beginning of the i-th sorting (i=1,2,3... n-1), the current ordered area and disordered area are R[1... i-1] and R[i... n] respectively.
In this sequence, the record R[k] with the smallest keyword is selected from the current unordered area, and the record subscript k is exchanged with the first record R[i] in the unordered area, so that R[1... I] and R[i+1... n) become a new ordered area with an increase in the number of records and a new unordered area with a decrease in the number of records respectively;
After n-1 times, the sorting is completed.
characteristic:
One of the most stable sorting algorithms, because no matter what data goes in, it is O(n2) time complexity, so when using it, the smaller the data scale, the better. The only benefit may be that it does not take up additional memory space.
Implementation code:
function selectionSort(arr) {
var len = arr.length;
var minIndex, temp;
for (var i = 0; i < len - 1; i++) {
minIndex = i;
for (var j = i + 1; j < len; j++) {
if (arr[j] < arr[minIndex]) { // Find the smallest number
minIndex = j; // Save the index of the smallest number
}
}
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}
3. Insertion Sort
The algorithm description of insertion sort is a simple and intuitive sorting algorithm. Its working principle is to build an ordered sequence, scan the unordered data from back to front in the sorted sequence, find the corresponding position and insert it.
Algorithm description:
Starting from the first element, the element can be considered to have been sorted;
Take out the next element and scan from back to front in the sorted element sequence;
If the element (sorted) is larger than the new element, move the element to the next position;
Repeat step 3 until the sorted element is found to be less than or equal to the position of the new element;
After inserting the new element into this position;
Repeat steps 2 to 5.
characteristic:
In the implementation of insertion sort, in place sort is usually adopted (that is, the sort that only needs the additional space of O(1)). Therefore, in the process of scanning from back to front, the sorted elements need to be moved back step by step to provide insertion space for the latest elements.
Code implementation:
function insertionSort(arr) {
var len = arr.length;
var preIndex, current;
for (var i = 1; i < len; i++) {
preIndex = i - 1;
current = arr[i];
while (preIndex >= 0 && arr[preIndex] > current) {
arr[preIndex + 1] = arr[preIndex];
preIndex--;
}
arr[preIndex + 1] = current;
}
return arr;
}
4. Sort (Shell Sort)
In 1959, Shell invented the first sorting algorithm to break through O(n^2), which is an improved version of simple insertion sorting. It differs from insert sorting in that it preferentially compares elements that are far away. Hill sort is also called reduced incremental sort.
Algorithm description:
First, divide the whole record sequence to be sorted into several subsequences for direct insertion sorting. The specific algorithm description is as follows:
t1, tk, tk = t1, tk = t2;
Sort the sequence k times according to the number of incremental sequences k;
For each sorting, the sequence to be sorted is divided into several subsequences with length m according to the corresponding increment ti, and each sub table is directly inserted and sorted. Only when the increment factor is 1, the whole sequence is treated as a table, and the table length is the length of the whole sequence.
Code implementation:
function shellSort(arr) {
var len = arr.length;
for (var gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
// Note: This is different from the dynamic diagram. The dynamic diagram is executed in groups, and the actual operation is that multiple groups are executed alternately
for (var i = gap; i < len; i++) {
var j = i;
var current = arr[i];
while (j - gap >= 0 && current < arr[j - gap]) {
arr[j] = arr[j - gap];
j = j - gap;
}
arr[j] = current;
}
}
return arr;
}
5. Merge Sort
Merge sort is an effective sort algorithm based on merge operation. The algorithm is a very typical application of Divide and Conquer. Merge the ordered subsequences to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one, it is called 2-way merging.
Algorithm description:
The input sequence with length n is divided into two subsequences with length n/2;
Merge and sort the two subsequences respectively;
Merge the two sorted subsequences into a final sorting sequence.
Algorithm analysis:
Merge sort is a stable sort method. Like selective sorting, the performance of merge sorting is not affected by the input data, but it is much better than selective sorting, because it is always O(nlogn) time complexity. The cost is the need for additional memory space.
Code implementation:
function mergeSort(arr) {
var len = arr.length;
if (len < 2) {
return arr;
}
var middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
var result = [];
while (left.length>0 && right.length>0) {
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length)
result.push(left.shift());
while (right.length)
result.push(right.shift());
return result;
}
6. Quick Sort
Basic idea of quick sort: divide the records to be arranged into two independent parts through one-time sorting. If the keywords of one part of the records are smaller than those of the other part, the records of these two parts can be sorted separately to achieve the order of the whole sequence.
Algorithm description:
Quick sort uses divide and conquer to divide a list into two sub lists. The specific algorithm is described as follows:
Pick out an element from the sequence, which is called "pivot";
Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition exits, the benchmark is in the middle of the sequence. This is called a partition operation;
Recursively sorts subsequences that are smaller than the reference value element and subsequences that are larger than the reference value element.
Code implementation:
function quickSort(arr, left, right) {
var len = arr.length,
partitionIndex,
left = typeof left != 'number' ? 0 : left,
right = typeof right != 'number' ? len - 1 : right;
if (left < right) {
partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex-1);
quickSort(arr, partitionIndex+1, right);
}
return arr;
}
function partition(arr, left ,right) { // Partition operation
var pivot = left, // Set reference value (pivot)
index = pivot + 1;
for (var i = index; i <= right; i++) {
if (arr[i] < arr[pivot]) {
swap(arr, i, index);
index++;
}
}
swap(arr, pivot, index - 1);
return index-1;
}
function swap(arr, i, j) {
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
7. Heap Sort
Heap sort refers to a sort algorithm designed by using the data structure of heap. Heap is a structure similar to a complete binary tree, and satisfies the nature of heap at the same time: that is, the key value or index of a child node is always less than (or greater than) its parent node.
Algorithm description:
Build the initial keyword sequence to be sorted (R1,R2,... Rn) into a large top heap, which is the initial unordered area;
Exchange the top element R[1] with the last element R[n], and obtain a new disordered region (R1,R2,... Rn-1) and a new ordered region (Rn), and meet R[1,2... N-1] < = R[n];
Since the new heap top R[1] may violate the nature of the heap after exchange, it is necessary to adjust the current unordered area (R1,R2,... Rn-1) to a new heap, and then exchange R[1] with the last element of the unordered area again to obtain a new unordered area (R1,R2,... Rn-2) and a new ordered area (Rn-1,Rn). Repeat this process until the number of elements in the ordered area is n-1, and the whole sorting process is completed.
Code implementation:
var len; // Because multiple functions declared need data length, set len as a global variable
function buildMaxHeap(arr) { // Build large top reactor
len = arr.length;
for (var i = Math.floor(len/2); i >= 0; i--) {
heapify(arr, i);
}
}
function heapify(arr, i) { // Heap adjustment
var left = 2 * i + 1,
right = 2 * i + 2,
largest = i;
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest);
}
}
function swap(arr, i, j) {
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
function heapSort(arr) {
buildMaxHeap(arr);
for (var i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i);
len--;
heapify(arr, 0);
}
return arr;
}
8. Counting Sort
Counting sort is not a sort algorithm based on comparison. Its core is to convert the input data values into keys and store them in the additional array space. As a sort with linear time complexity, count sort requires that the input data must be integers with a certain range.
Algorithm description:
Find the largest and smallest elements in the array to be sorted;
Count the number of occurrences of each element with value i in the array and store it in item i of array C;
All counts are accumulated (starting from the first element in C, and each item is added to the previous item);
Reverse fill the target array: put each element i in item C(i) of the new array, and subtract 1 from C(i) for each element.
Algorithm analysis:
Counting sorting is a stable sorting algorithm. When the input elements are n integers between 0 and K, the time complexity is O(n+k), and the space complexity is O(n+k). Its sorting speed is faster than any comparison sorting algorithm. When k is not very large and the sequence is relatively concentrated, counting sorting is a very effective sorting algorithm.
Code implementation:
function countingSort(arr, maxValue) {
var bucket = new Array(maxValue + 1),
sortedIndex = 0;
arrLen = arr.length,
bucketLen = maxValue + 1;
for (var i = 0; i < arrLen; i++) {
if (!bucket[arr[i]]) {
bucket[arr[i]] = 0;
}
bucket[arr[i]]++;
}
for (var j = 0; j < bucketLen; j++) {
while(bucket[j] > 0) {
arr[sortedIndex++] = j;
bucket[j]--;
}
}
return arr;
}
9. Bucket Sort
Bucket sorting is an upgraded version of counting sorting. It makes use of the mapping relationship of the function. The key to efficiency lies in the determination of the mapping function. Working principle of bucket sort: assuming that the input data is uniformly distributed, divide the data into a limited number of buckets, and then sort each bucket separately (it is possible to use another sorting algorithm or continue to use bucket sorting recursively).
Algorithm description:
Set a quantitative array as an empty bucket;
Traverse the input data and put the data into the corresponding bucket one by one;
Sort each bucket that is not empty;
Splice the ordered data from a bucket that is not empty.
algorithm analysis
In the best case, the linear time O(n) is used for bucket sorting. The time complexity of bucket sorting depends on the time complexity of sorting the data between buckets, because the time complexity of other parts is O(n). Obviously, the smaller the bucket division, the less data between buckets, and the less time it takes to sort. But the corresponding space consumption will increase.
Code implementation:
function bucketSort(arr, bucketSize) {
if (arr.length === 0) {
return arr;
}
var i;
var minValue = arr[0];
var maxValue = arr[0];
for (i = 1; i < arr.length; i++) {
if (arr[i] < minValue) {
minValue = arr[i]; // Minimum value of input data
} else if (arr[i] > maxValue) {
maxValue = arr[i]; // Maximum value of input data
}
}
// Initialization of bucket
var DEFAULT_BUCKET_SIZE = 5; // Set the default number of buckets to 5
bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
var buckets = new Array(bucketCount);
for (i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
// The mapping function is used to allocate the data to each bucket
for (i = 0; i < arr.length; i++) {
buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
}
arr.length = 0;
for (i = 0; i < buckets.length; i++) {
insertionSort(buckets[i]); // Sort each bucket. Insert sort is used here
for (var j = 0; j < buckets[i].length; j++) {
arr.push(buckets[i][j]);
}
}
return arr;
}
10. Radix Sort
Cardinality sorting is to sort first according to the low order, and then collect; Then sort according to the high order, and then collect; And so on until the highest position. Sometimes some attributes have priority order. They are sorted by low priority first, and then by high priority. The final order is high priority, high priority first, high priority with the same low priority, high priority first.
Algorithm description:
Get the maximum number in the array and get the number of bits;
arr is the original array, and each bit is taken from the lowest bit to form a radio array;
Count and sort the radix (using the characteristics that count sorting is suitable for a small range of numbers);
Algorithm analysis:
Cardinality sorting is based on sorting separately and collecting separately, so it is stable. However, the performance of cardinality sorting is slightly worse than bucket sorting. Each bucket allocation of keywords requires O(n) time complexity, and obtaining a new keyword sequence after allocation requires O(n) time complexity. If the data to be arranged can be divided into D keywords, the time complexity of cardinality sorting will be O(d*2n). Of course, D is far less than N, so it is basically linear.
The spatial complexity of cardinality sorting is O(n+k), where k is the number of buckets. Generally speaking, n > > k, so about n additional spaces are needed.
Code implementation:
var counter = [];
function radixSort(arr, maxDigit) {
var mod = 10;
var dev = 1;
for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
for(var j = 0; j < arr.length; j++) {
var bucket = parseInt((arr[j] % mod) / dev);
if(counter[bucket]==null) {
counter[bucket] = [];
}
counter[bucket].push(arr[j]);
}
var pos = 0;
for(var j = 0; j < counter.length; j++) {
var value = null;
if(counter[j]!=null) {
while ((value = counter[j].shift()) != null) {
arr[pos++] = value;
}
}
}
}
return arr;
}