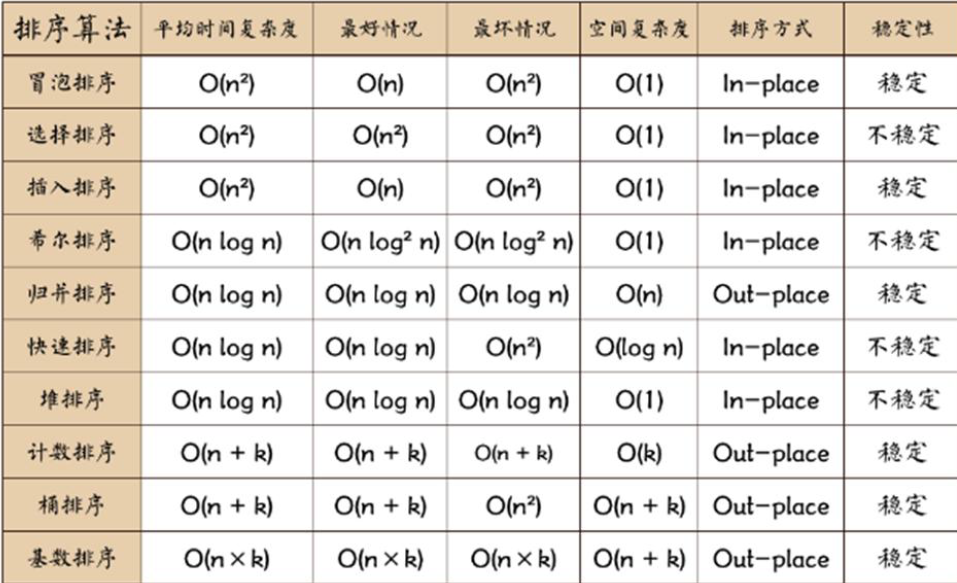
Sorting algorithm summary
1. Comparison of various sorting algorithms
Compare the current mainstream sorting algorithms:
Of which:
1. Stability: indicates that if a before sorting was originally in front of b and a=b, after sorting, a is still in front of b;
2. Instability: Contrary to the above;
3. Internal sorting: all sorting is completed in memory;
4. External sorting: due to the large amount of sorted data, the data can be placed on the disk, and the sorting can only be carried out through the data transmission in the disk memory (Note: the following sorts are internal sorting);
5. Time complexity: the time spent in the execution of an algorithm: expressed in O(f(n)), where f(n) is a function of data scale n;
6. Space complexity: the size of memory required to run a program;
7.n: data scale;
8.k: number of barrels;
In place: no additional memory;
10; Out place: taking up extra memory
2. Exchange type sorting algorithm
2.1 Bubble Sort algorithm
/**
* Created by FengBin on 2020/10/28 15:20
* Bubble sorting algorithm: stable sorting
* Time complexity T(n): optimal time complexity O(n), average time complexity O(n^2), and worst time complexity O(n^2)
*/
public class BubbleSorting {
public static void main(String[] args) {
int[] arr = {-9,78,0,23,-567,70};
int n = arr.length;
for (int i = 0; i < n - 1; i++) { //n- 1 sorting is required
for (int j = 0; j < n - 1 - i; j++) {//[0,n - 1 - j] are compared. If the former is greater than the latter, the positions of the former and the latter are exchanged in order
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
System.out.println("The array after bubble sorting is :" + Arrays.toString(arr));
}
}
2.2 Quick Sort algorithm
Quick sort idea:
Quick sort is also an exchange sort, which is an improvement on bubble sort. It defines an element of an array as the benchmark value, and divides the data to be sorted into two independent parts after one sort. All the data in one part is less than the benchmark value, and the data in the other part is greater than the benchmark value, Then the two parts are sorted quickly according to this method. The whole sorting process is recursive, and finally all data become an ordered sequence
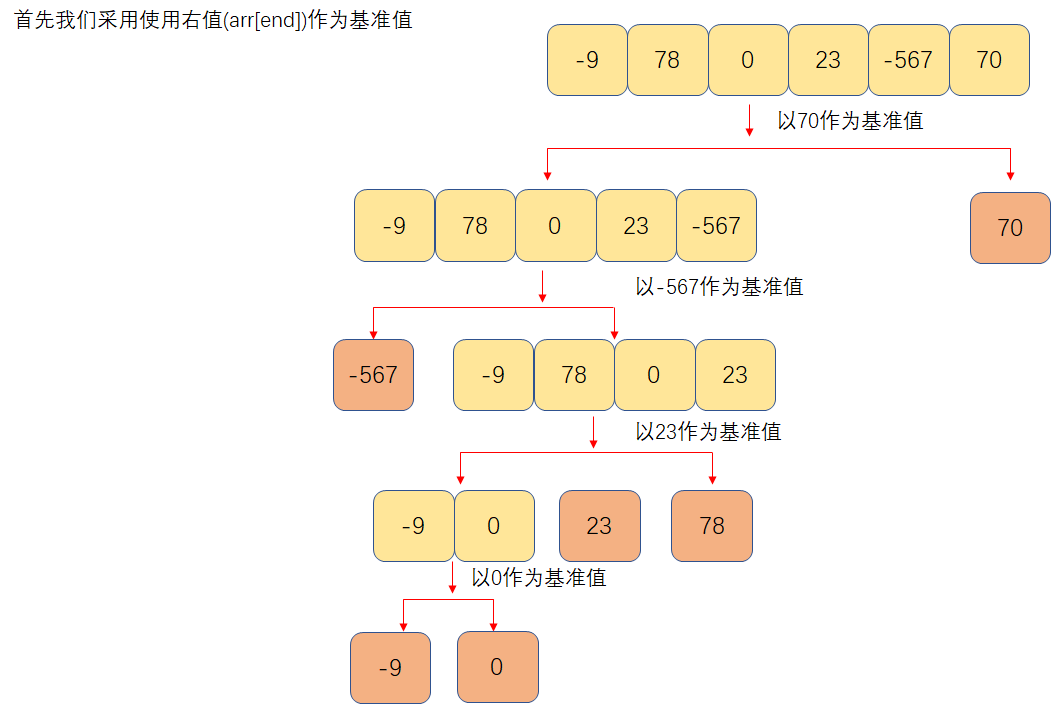
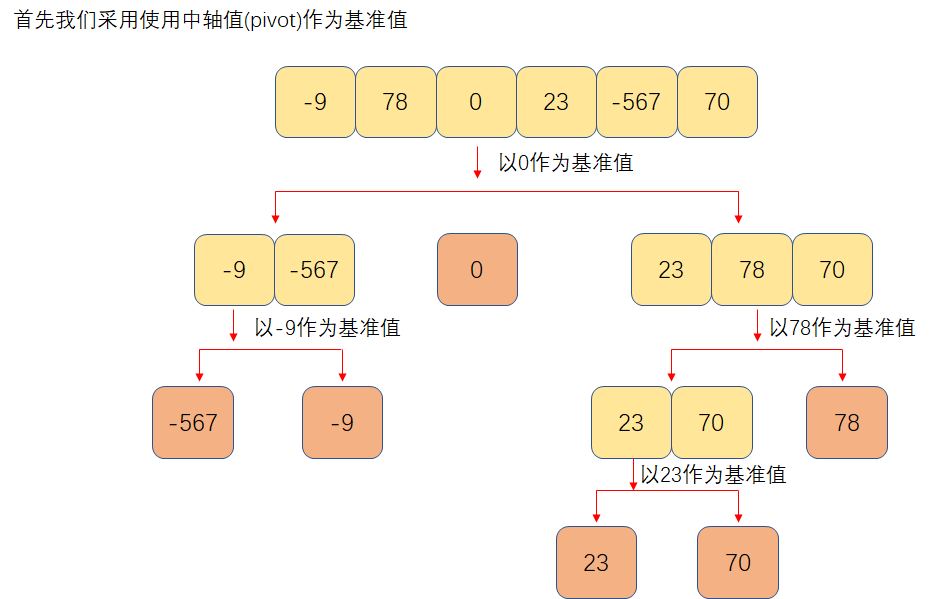
Next, we give the illustration and code implementation of the quick sorting algorithm by taking the defined reference value as the first value, the middle axis value and the end value as examples respectively;
The quick sort algorithm belongs to unstable sorting:
Time complexity T(n): optimal time complexity O(nlogn), worst time complexity O(n^2), average time complexity O(nlogn)

Summary:
Quick sort idea:
First, we define start=0,end=arr.length-1;
Perform while quick sort operation: condition [start! = end]
If start > end: indicates the end of sorting and returns directly
We first define the base value [base]
Redefine the auxiliary variables left = start,right = end,temp;
(1) We define the reference value as the leftmost value
At this time, we first find the first number less than the benchmark value from the right, and then find the first number greater than the benchmark value from the left
Then perform the number exchange operation
When exiting the while loop, the left index is located at the last position less than the reference value. We exchange its position with the reference value and place the reference value in the middle
Then, the quick sort operation to the left and right of the benchmark value is performed recursively
(2) We define the reference value as the rightmost value
At this time, we first find the first number greater than the benchmark value from the left, and then find the first number less than the benchmark value from the right
Then perform the number exchange operation
When exiting the while loop, the right index is at the first position greater than the reference value. We exchange its position with the reference value and place the reference value in the middle
Then, the quick sort operation to the left and right of the benchmark value is performed recursively
be careful:
(1) If we search from the left and then from the right, then the benchmark value is exchanged with the right index
(2) If we search from the right and then from the left, the benchmark value will be exchanged with the left index
java code implements the above three forms of quick sorting
Take the left value as the reference value
public class QuickSorting {
public static void main(String[] args) {
int[] nums = {-9,78,0,23,-567,70};
quickSort(nums,0,nums.length - 1);
System.out.println("The array after quick sorting is:" + Arrays.toString(nums));
}
//Take the left value as the reference value
public static void quickSort(int[] nums, int start, int end) {
//If start > end: is not satisfied, return directly
if (start >= end) return;
//Take the left value as the reference value
int base = nums[start];
//Define two pointer variables, pointing to start and end respectively
int left = start;
int right = end;
while (left != right) {
//Order is very important. First find a number [must] smaller than the benchmark value from the right
while (left < right && nums[right] >= base) {
--right;
}
//Then find a number larger than the reference value from the left
while (left < right && nums[left] <= base) {
++left;
}
//At this time, judge whether left is less than right
if (left < right) {
//Swap the position of two numbers in the array
swap(nums,left,right);
}
}
//Place the reference value at the index position of left [that is, there is the last position less than base, so that the left side of the reference value is less than it and the right side is less than it]
swap(nums,start,left);
//Then perform a quick sort recursively
quickSort(nums,start,left - 1);
quickSort(nums,left + 1,end);
}
public static void swap(int[] nums,int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
Take the right value as the reference value
public class QuickSorting {
public static void main(String[] args) {
int[] nums = {-9,78,0,23,-567,70};
quickSort(nums,0,nums.length - 1);
System.out.println("The array after quick sorting is:" + Arrays.toString(nums));
}
//Take the right value as the reference value
public static void quickSort(int[] nums, int start, int end) {
//If start > end: is not satisfied, return directly
if (start >= end) return;
//Take the left value as the reference value
int base = nums[end];
//Define two pointer variables, pointing to start and end respectively
int left = start;
int right = end;
while (left != right) {
//Order is very important. You must first find a number greater than the benchmark value from the left
while (left < right && nums[left] <= base) {
++left;
}
//Then find a number less than the reference value from the right
while (left < right && nums[right] >= base) {
--right;
}
//At this time, judge whether left is less than right
if (left < right) {
//Swap the position of two numbers in the array
swap(nums,left,right);
}
}
//Place the reference value at the index position of left [that is, there is the last position less than base, so that the left side of the reference value is less than it and the right side is less than it]
swap(nums,end,right);
//Then perform a quick sort recursively
quickSort(nums,start,right - 1);
quickSort(nums,right + 1,end);
}
public static void swap(int[] nums,int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
//The central axis value is used as the reference value -- it is realized by another method, which has not been realized yet
3. Insert Sort algorithm
3.1 Direct Insert Sort algorithm

Figure out the direct insertion sorting process of arr={8,5,7,2,9,3,1}
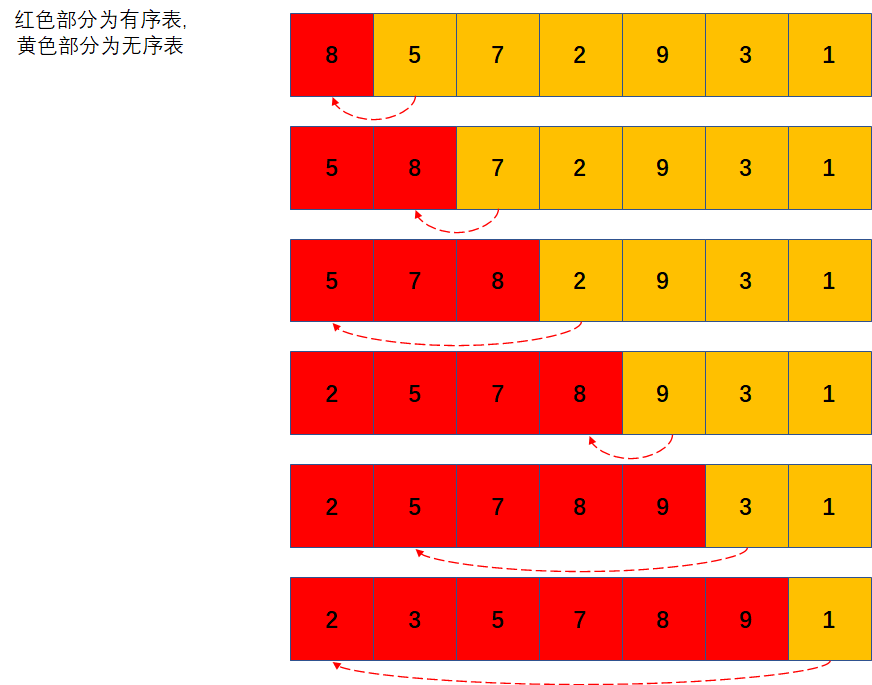
java code implementation of direct insertion sorting algorithm
public class InsertSorting {
/*
* Insertion sorting algorithm: time complexity T(n): optimal time complexity: O(n), worst time complexity: O(n^2), average time complexity: O(n^2)
* */
public static void main(String[] args) {
int[] nums = {65,789,-23,2,2,15,-56,60};
insertSort(nums);
System.out.println("The array after direct insertion and sorting is:" + Arrays.toString(nums));
}
private static void insertSort(int[] nums) {
int n = nums.length;
for (int j = 1; j < n; j++) { //Unordered set index subscript: [1,n - 1]
int insert = nums[j];
int i = j - 1;
while (i >= 0 && nums[i] > insert) {
nums[i + 1] = nums[i];
--i;
}
//Exit the while loop. At this time, the position of i + 1 is the position of insert
nums[i + 1] = insert;
}
}
}
3.2 Hill sorting algorithm Shell Sort
Hill sorting algorithm:
Direct insertion sorting algorithm, if sorting from small to large, and the smaller number is at the end of the array, it will greatly increase the number of comparisons and increase the time spent;
This paper introduces a more efficient insertion sorting algorithm - Hill sorting algorithm
T(n): optimal time complexity O(nlogn), average time complexity O(nlogn), worst time complexity O(nlogn)
Basic realization idea:
Hill sorting is to group the array elements to be sorted according to a certain increment of the subscript, and then sort the groups using the direct insertion sorting algorithm;
In this way, with the gradual reduction of increment, each group contains more and more keywords; When the increment is reduced to 1, the whole array is divided into 1 group, and the sorting is completed;
We explain Hill's thought through diagrams:
Define the array to be sorted arr = {8,9,1,7,2,3,5,4,6,0}, and sort it from small to large. The following is the graphic analysis process:

java code implementation:
/**
* Created by FengBin on 2020/10/26 14:49
* Hill sorting: upgrade optimized insertion sorting algorithm: time complexity T(n): optimal time complexity: O(nlogn), worst time complexity: O(nlogn), average time complexity: O(nlogn)
* It belongs to unstable sorting algorithm
*/
public class ShellSorting {
public static void main(String[] args) {
int[] nums = {8,9,1,7,2,3,5,4,6,0};
//Hill sorting by exchange method
int temp = 0;
for (int gap = nums.length / 2; gap > 0; gap /= 2) {
//The initial value of gap is num Length / 2, and then decrease to the original 1 / 2
for (int i = gap; i < nums.length; i++) {
//Traverse gap to the last element of the array: complete the internal insertion sorting of the array into gap groups
for (int j = i - gap; j >= 0; j -= gap) {
if (nums[j] > nums[j + gap]) {
temp = nums[j];
nums[j] = nums[j + gap];
nums[j + gap] = temp;
}
}
}
}
//At the end of the for loop, the array nums is sorted from small to large
System.out.println("nums Array sorted : " + Arrays.toString(nums));
//Hill sorting is realized by moving method (this implementation method is recommended)
public static void shellSort(int[] nums) {
int n = nums.length;
//Incremental gap: start from half of the array and process in half until 1 stops
for (int gap = n / 2; gap > 0; gap /= 2) {
//There is a direct insertion sort interspersed here, but the starting position here changes from 1 to gap, and moving forward one bit below changes to moving gap bit
for (int j = gap; j < n; j++) {
int insert = nums[j];
int i = j - gap;
while (i >= 0 && nums[i] > insert) {
nums[i + gap] = nums[i];
i -= gap;
}
//Exit the while loop, and i + gap is the insert ion position
nums[i + gap] = insert;
}
}
}
}
4. Select Sort Algorithm
4.1 Simple Select Sort Algorithm
Simple selection sort: unstable sort
Time complexity T(n): optimal time complexity O(n2), worst time complexity O(n2), average time complexity O(n^2)
Basic idea of simple selection sorting:
Select an element from the pre sorted array according to the specified rules, and then exchange positions according to the regulations to achieve the purpose of sorting
For an arr array: assume a total of n elements
The first time: select a minimum (large) value from arr[0] ~ arr[n-1] and exchange it with arr[0]
The second time: select a minimum (large) value from arr[1] ~ arr[n-1] and exchange it with arr[1]
...
The N-1 time: select the minimum (large) value from arr[n-2] ~ arr[n-1] and exchange it with arr[n-2]
A total of n-1 selections are required to obtain an ordered sequence that requires sorting from small to large (from large to small)
be careful:
1. Select sorting. There are (array size – 1) rounds of sorting
2. Each round of sorting is a cycle. The rules of the cycle are as follows:
- Let's first assume that the current value is the minimum (large) number
- Then compare with each subsequent number. If it is found that there is a smaller (larger) number than the current number, update the minimum (larger) value and obtain its subscript
- When traversing to the end of the array, we get the minimum (large) number of this round and its subscript
- Then the exchange operation is carried out
We use arr={8,9,1,7,2,3} to analyze the graphical process of simple selection and sorting:
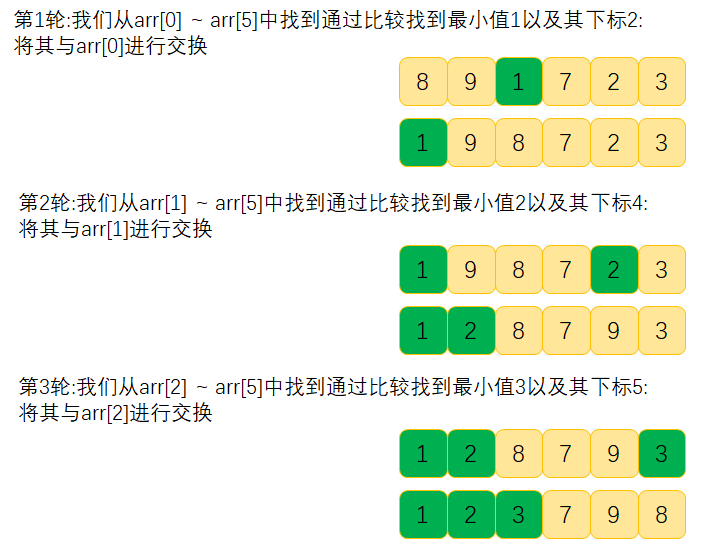

java code implements simple selection sorting:
/**
* Created by FengBin on 2020/10/26 15:25
* Select sorting algorithm: it belongs to unstable sorting algorithm
* Time complexity T(n): optimal time complexity: O(n^2), worst time complexity: O(n^2), average time complexity: O(n^2)
*/
public class SelectSorting {
public static void main(String[] args) {
int[] arr = {8,9,1,7,2,3};
//Select Sorting: through continuous comparison: update the array 0,1,2, The value of the arr.length-2 index. After sorting the current n - 1 values, the last value must be ordered
for (int i = 0; i < arr.length - 1; i++) {
//First assume that the current value is the minimum value and record its subscript
int minIndex = i;
int min = arr[i];
for (int j = i + 1; j < arr.length; j++) {
if (min > arr[j]) {
min = arr[j];//Update the minimum value of this round
minIndex = j;//At the same time, the subscript of the minimum value is updated
}
}
//If the index value of [Mini] changes, we will exchange it with the minimum value of the current index
if (minIndex != i) {
arr[minIndex] = arr[i];
arr[i] = min;
}
}
}
}
4.2 heap sorting algorithm
Basic introduction to heap sorting:
1) Heap sort is a sort algorithm designed by using heap data structure. Heap sort belongs to selective sort. Its worst, best and average time complexity are O(nlogn). It is an unstable sort algorithm
2) Heap is a complete binary tree with the following properties:
Each node is greater than or equal to the val value of its left and right child nodes, which is called large top heap
Each node is less than or equal to the val value of its left and right child nodes, which is called small top heap
Examples of large top pile and small top pile are shown in the figure below:

Taking the large top heap as an example, we number the vertices in the heap according to layers, and then map them to the array. The characteristics of the corresponding large top heap are as follows:
a
r
r
[
i
]
>
=
a
r
r
[
2
∗
i
+
1
]
and
And
a
r
r
[
i
]
>
=
a
r
r
[
2
∗
i
+
2
]
his
in
i
yes
answer
The first
A few
individual
section
spot
,
from
0
open
beginning
enter
that 's ok
Compile
number
Arr [i] > = arr [2 * I + 1] and arr [i] > = arr [2 * I + 2], where I corresponds to the first node and is numbered from 0
Arr [i] > = arr [2 * i+1] and arr [i] > = arr [2 * i+2] where I corresponds to the first node and is numbered from 0

Similarly, the characteristics of small top reactor are:
a
r
r
[
i
]
<
=
a
r
r
[
2
∗
i
+
1
]
and
And
a
r
r
[
i
]
<
=
a
r
r
[
2
∗
i
+
2
]
his
in
i
yes
answer
The first
A few
individual
section
spot
,
from
0
open
beginning
enter
that 's ok
Compile
number
Arr [i] < = arr [2 * I + 1] and arr [i] < = arr [2 * I + 2], where I corresponds to the first node and is numbered from 0
Arr [i] < = arr [2 * i+1] and arr [i] < = arr [2 * i+2], where I corresponds to the first few nodes and is numbered from 0
be careful:
- We choose the sorting algorithm to use the large top heap in ascending order and the small top heap in descending order
Basic idea of heap sorting:
-
Construct a large top heap of the sequence to be sorted (assuming n elements) [array implementation, that is, use our order to store the binary tree]
-
At this point, the maximum value of the whole sequence is the root node at the top of the heap
-
Swap it with the end element, where the end is the maximum value
-
Then, n-1 elements are reconstructed into a large top heap, so that the sub small value of the sequence can be obtained. After repeated execution, an ordered sequence can be obtained
-
The number of final elements (large top heap) is less and less, and finally an ascending ordered sequence is obtained
Note: with the same idea, we build a small top heap, that is, we can get a descending ordered sequence
Graphic thinking analysis:
Step 1: construct the initial heap. The given disordered sequence is constructed into a large top heap (generally, the large top heap is used in ascending order and the small top heap is used in descending order).
- Suppose that the structure of a given unordered sequence is as follows
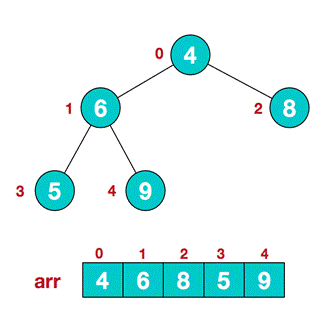
- At this time, we start from the last non leaf node (the leaf node does not need to be adjusted naturally. The first non leaf node arr.length/2-1=5/2-1=1, that is, the 6 nodes below), and adjust from left to right and from bottom to top.
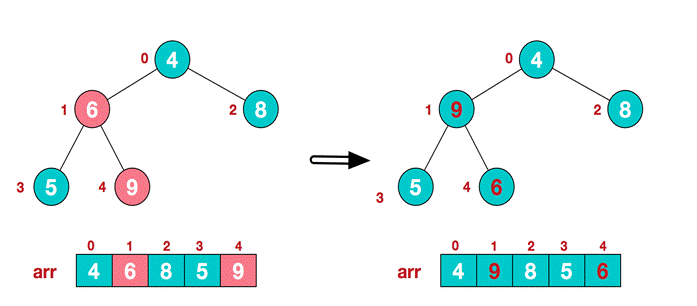
- . find the second non leaf node 4. Since the 9 element in [4,9,8] is the largest, 4 and 9 exchange.
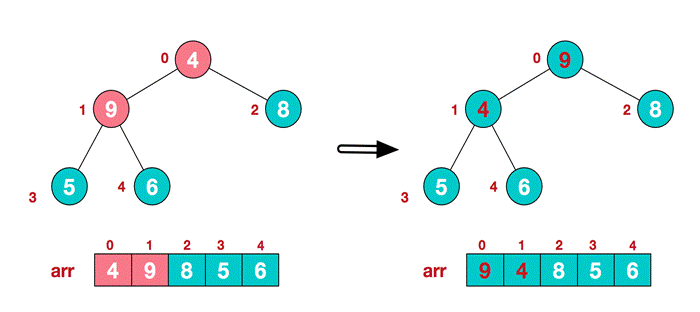
- At this time, the exchange leads to the confusion of the structure of the sub root [4,5,6]. Continue to adjust. 6 is the largest in [4,5,6], and exchange 4 and 6.
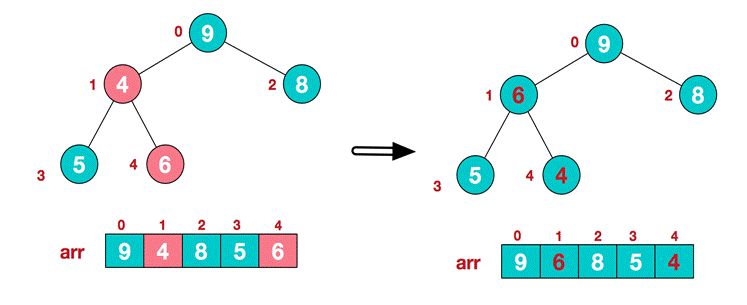
At this point, we construct an unordered sequence into a large top heap.
In step 2, the top element of the heap is exchanged with the last element to maximize the last element. Then continue to adjust the heap, and then exchange the top element with the end element to get the second largest element. Such repeated exchange, reconstruction and exchange.
- . swap top element 9 and end element 4
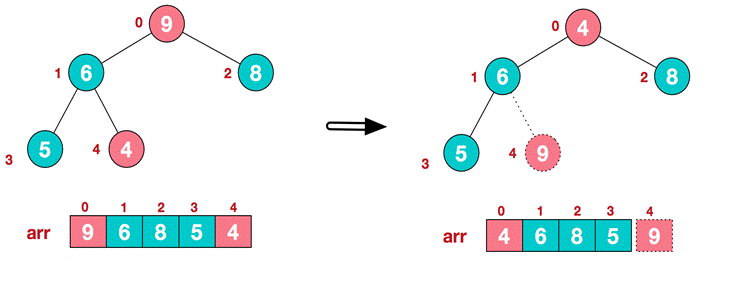
- . restructure to continue to meet the heap definition
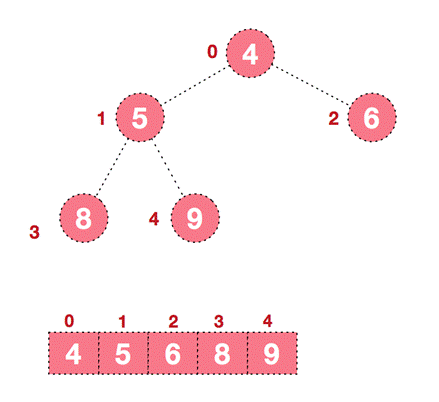
- . then exchange the top element 8 with the end element 5 to obtain the second largest element 8

- In the subsequent process, continue to adjust and exchange, so as to make the whole sequence orderly
Code implementation:
public class HeapSorting {
public static void main(String[] args) {
int[] arr = {4,6,8,5,9};
heapSort(arr);
System.out.println("Sorted array arr: " + Arrays.toString(arr));
}
//Defines the main method for heap sorting
public static void heapSort(int[] arr) {
//Define an auxiliary variable: used to adjust the exchange of array elements after the large top heap
int temp = 0;
//Step 1: adjust the whole binary tree to a large top heap
for (int i = arr.length / 2 - 1; i >= 0 ; i--) {
adjustHeap(arr,i,arr.length);
}
//After the first operation, the array binary tree becomes a large top heap. We exchange the top of the binary tree [i.e. the first element of the array] with the last element of the array to be sorted to complete the placement of the current maximum value
//Step 2: execute the operation of adjusting the large top heap in a loop. After each adjustment, exchange the maximum value. As the number of elements adjusted becomes less and less, finally complete the sorting of the array
for (int i = arr.length - 1; i > 0; i--) {
//Swap the maximum value to the end of the array
temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
//Adjust the large top heap of the remaining arrays
adjustHeap(arr,0,i);
}
}
//Adjust an array (corresponding to a binary tree) to a large top heap: adjust the subtree structure of non leaf nodes corresponding to i to a large top heap
//arr: refers to the passed in array to be adjusted; i represents the index of the non leaf node in the array; length indicates how many elements are adjusted [gradually reduced]
public static void adjustHeap(int[] arr,int i,int length) {
//Step 1: get the value of the current i index position and save it to a temporary variable
int temp = arr[i];
//Step 2: start to adjust the subtree with the i index position as the root node: adjust it to a large top heap
//Where k = 2 * i + 1,k represents the left child node of i node. If it is less than length, the next cycle is the left child node of K node
for (int k = 2 * i + 1; k < length; k = 2 * k + 1) {
//k + 1 is the right child of node i
if (k + 1 < length && arr[k] < arr[k + 1]) {
//If the value of the left child node is less than the value of the right child node
k++;
}
if (arr[k] > temp) {
//If the value of the child node is greater than the value of the parent node, the larger value is assigned to the parent node
arr[i] = arr[k];
//And assign k to i to continue the cyclic comparison [this step is very important!!!]
i = k;
}else {
//If the child node is less than or equal to the value of the parent node, no exchange is required
break;
}
}
//At the end of the for loop, the maximum value of the subtree with i as the parent node has been placed at the root node [top] of the subtree
//Step 3: put the value of temp at the position of I at this time [i.e. after adjustment]
arr[i] = temp;
}
}
5. Merge Sort algorithm
Basic idea: the algorithm adopts the classical divide and conquer strategy: divide and conquer is to divide the problem into some small problems and then solve them recursively, while conquer is to "patch" the answers obtained in different stages, that is, divide and conquer;
Where Java arrays By default, merge sort () adopts merge algorithm. Merge sort is another sort method different from insert sort, exchange sort and selection sort. Merging means merging two or more ordered tables into a new ordered table.
Merge sort includes multi-channel merge sort and two-way merge sort, which can be used for internal sort or external sort. Here, only the two-way merging method of inner sorting is discussed.
1. Two way merging sorting algorithm:
N records are regarded as n ordered sub tables with length 1; Merge the record keywords in order to obtain n/2 ordered sub tables with a length of 2; Repeat step until all records are merged into an ordered table with length n.
2. Implementation of the algorithm
(two-way merging) the implementation of this algorithm is not as simple as that shown in the figure. It is discussed in three steps. First, from a macro perspective, let the sub table length L=1 for processing; Continuously make L=2L and process the sub table until l > = n. write this process as a main framework function mergeport. Then, for a certain sub table length L, divide n records into several groups of sub tables and merge them in pairs. Here, it is obvious to cycle several times. Write this step as a function mergepass, which can be called by mergeport. Finally, let's look at the merging of each group (pair) of sub tables. The principle is the same, but the sub table table length is different. In other words, the first record number and the last record number of the sub table are different. Take the merging operation as the core algorithm and write it into the function merge, which is called by mergepass. Assuming that we have a sequence that is not well ordered, we first use the segmentation method to divide the sequence into ordered subsequences, and then use the merging method to merge the subsequences into ordered sequences. The process of segmentation and merging can be seen in the following illustration.
3. Time complexity and space complexity calculation
Time complexity analysis of merging algorithm: mainly considering the time cost of two functions,
1, Array partition function sortArrays(); 2, Ordered array merge function mergeArrays();
The time complexity of mergeArrays() is O(n). Because there are two loops with length n (non nested) in the code, the time complexity is O(n);
The time T[n] consumed by merging and sorting with element length n under simple analysis
Call sortArrays() to divide the function into two parts, and the time taken to sort each small part is T[n/2],
Finally, the two ordered arrays are combined into an ordered array_ The time taken by the mergeSort() function is O(n);
Formula: T[n] = 2T[n/2] + O(n);
The formula is not carefully deduced. You can refer to the following: rapid sorting of sorting algorithm and the derivation of time complexity in time complexity and space complexity
So the result is: T[n] = O(nlogn)
The space complexity of merging is the space occupied by the temporary array and the data pushed into the stack during recursion: n + logn; Therefore, the spatial complexity is: O(n);
4. Summary:
Although merging sorting is relatively stable, it is also very effective in time (the worst time complexity and the optimal time complexity are O(nlogn),
However, this algorithm consumes a lot of space. Generally speaking, this method is not used for internal sorting, but quick sorting; External sorting will consider using this method;
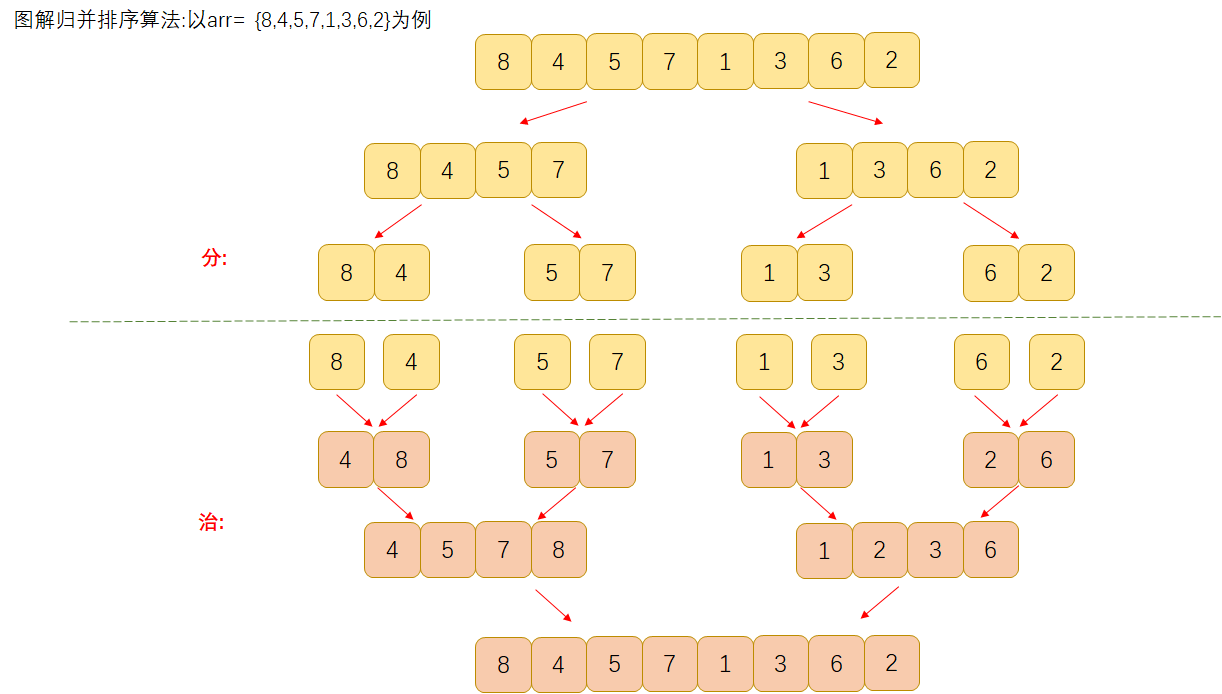
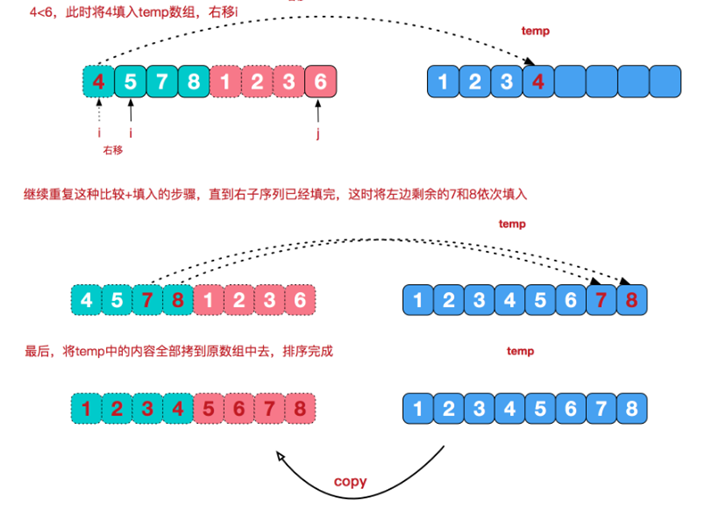
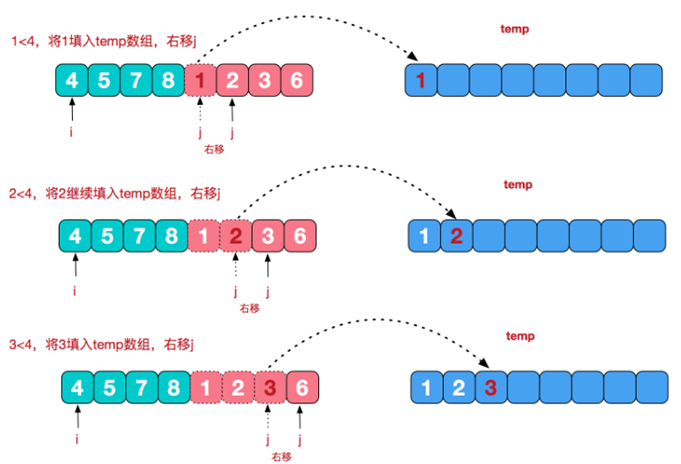
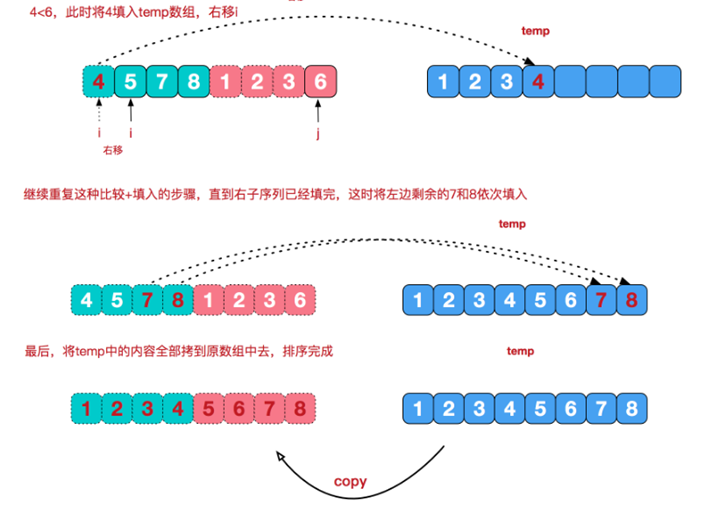
We illustrate the process of the last merge:
Step 1: fill the data of the left and right sides (ordered array) into the temp array according to the rules from small to large until one side of the left and right sides is processed;
Step 2: save one side of the remaining data to the temp array in turn;
Step 3: copy all the temp array elements to the arr original array
java code implements merge sorting algorithm:
/**
* Created by FengBin on 2020/10/28 13:53
* Merge sorting algorithm: a stable sorting algorithm
* Time complexity T(n): optimal time complexity O(nlogn), worst time complexity O(nlogn), average time complexity O(nlogn)
*/
public class MergeSorting {
public static void main(String[] args) {
int[] nums = {65,789,-23,2,2,15,-56,60};
mergeSort(nums,0,nums.length - 1);
System.out.println("After merging and sorting nums Array:" + Arrays.toString(nums));
}
private static void mergeSort(int[] nums, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(nums,left,mid);
mergeSort(nums,mid + 1,right);
merge(nums,left,mid,right);
}
}
//Merging method
private static void merge(int[] nums, int left, int mid, int right) {
//Define an auxiliary array
int[] temp = new int[nums.length];
//Define index pointer pointing to left index position [start index of temp array]
int index = left;
//Then define two pointer variables pre - > left; next->mid + 1;
int pre = left;
int next = mid + 1;
while (pre <= mid && next <= right) {
if (nums[pre] <= nums[next]) {
temp[index++] = nums[pre++];
}else {
temp[index++] = nums[next++];
}
}
while (pre <= mid) {
temp[index++] = nums[pre++];
}
while (next <= right) {
temp[index++] = nums[next++];
}
//Copy and assign the elements of temp array to num array
index = left;
while (index <= right) {
nums[index] = temp[index];
index++;
}
}
}
6. Radix Sort algorithm
Cardinality sorting algorithm idea: stable sorting algorithm
Time complexity T(n): optimal time complexity O(n x k), average time complexity O(n x k), worst time complexity O(n x k), where k is the number of barrels
It belongs to "distribution sort", also known as bucket sort, through the value of each bit of the key value Assigning the elements to be sorted to some buckets has achieved the purpose of sorting The bucket is realized by one-dimensional array
Basic idea:
All arrays to be compared shall be unified into the same digit length, and the zero filling operation shall be carried out in front of the shorter digit, and then the next bit shall be compared successively from the lowest bit. In this way, after sorting from the lowest bit to the highest bit, the whole sequence will become an ordered sequence

java code implements cardinality sorting algorithm:
/**
* Created by FengBin on 2020/10/28 14:26
* Cardinality sorting algorithm: a stable sorting algorithm
* Time complexity T(n): optimal time complexity O(n x k), average time complexity O(n x k), worst time complexity O(n x k), where k is the number of barrels
*/
public class RadixSorting {
public static void main(String[] args) {
int[] arr = {53,3,542,748,14,214};
radixSort(arr);
System.out.println("The array after cardinality sorting is:" + Arrays.toString(arr));
}
private static void radixSort(int[] arr) {
//According to the passed in array, we first need to get the number of digits of the highest digit
int max = arr[0];
for (int i = 0; i < arr.length; i++) {
if (arr[i] > max)
max = arr[i];
}
//Get the highest number of digits
int maxDigit = (max + "").length();
//Define ten buckets: each bucket is a one-dimensional array:
//1. Because ten buckets are defined, the number of rows of the two-dimensional array is 10, that is, it contains ten one-dimensional arrays
//2. In order to prevent data overflow, the size of each one-dimensional array (i.e. the size of the bucket) is defined as the length of the array to be compared, arr.length
//3. Cardinality sorting: the classical space for time sorting algorithm
int[][] bucket = new int[10][arr.length];
//In order to record how many data are stored in real time in each of the ten buckets
//We define a one-dimensional array to record the number of data put into each bucket, bucketElementCount
int[] bEC = new int[10];
for (int i = 0,n = 1; i < maxDigit; i++,n *= 10) {
//Sort the number of bits corresponding to the element: single bit -- > ten bit -- > hundred bit
//Take out the value of the corresponding bit of each element
for (int j = 0; j < arr.length; j++) {
int digitOfEle = arr[j] / n % 10;
//Put it into the corresponding bucket
bucket[digitOfEle][bEC[digitOfEle]] = arr[j];
//Add 1 to the number of elements stored in the bucket
bEC[digitOfEle]++;
}
//At the end of the above for loop, all arr elements have been placed in different buckets according to the size of the corresponding bit value
//We then put the data in the bucket into the original array in order
int index = 0;
for (int k = 0; k < 10; k++) {//Ten barrels
//If there are elements in the bucket
if (bEC[k] != 0) {
//Loop the bucket and store it in the arr array
for (int l = 0; l < bEC[k]; l++) {
arr[index++] = bucket[k][l];
}
}
//After each round, remember to set bEC[k] to zero to prepare for recording the number of higher and different values in the corresponding bucket in the next round
bEC[k] = 0;
}
}
}
}