1. Basic Principles

Heap sorting is to sort an unordered sequence by utilizing the characteristics of heap.

Characteristics of heap

The heap is divided into the largest heap and the smallest heap, which is actually a complete binary tree.

1. Maximum heap requires no fewer elements than its children

2. The minimum heap requires no more node elements than its left and right children.

They don't require anything about the size of the relationship between the right and left children. In fact, they are very understandable.

With the above definition, we can know that the element at the root node of the largest heap must be the maximum in the heap.

In fact, our heap sorting algorithm is to grasp this feature of heap, each time take the top of the heap element, put it at the end of the sequence, and then the remaining

The remaining elements are readjusted to the maximum heap, followed by analogy, and the sorted sequence is finally obtained.

basic thought

1. The initial sequence of keywords to be sorted (a1,a2,..., an) is constructed into a large-top heap, which is the initial unordered region.

2. By exchanging the top element a[1] with the last element a[n], a new disordered region (a1,a2,..., an_1) and a new ordered region (an) are obtained.

3. Since the new top a[1] may violate the nature of the heap after exchange, it is necessary to adjust the current disordered region (a1,a2,, an_1) to a new heap, and then exchange a[1] with the last element of the disordered region to obtain a new disordered region (a1,a2,, an_2) and a new ordered region (an_1,an_2). Repeat this process until the number of elements in the ordered region is n-1, then the whole ordering process is completed.

An example

Here's an unordered sequence, [16, 7, 3, 20, 17, 8]

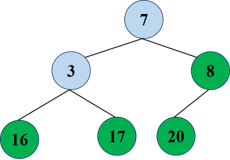
Firstly, a binary tree is constructed.

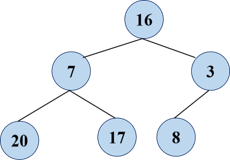
Then, according to the constructed binary tree, adjust from bottom to top to get an initialized maximum heap.

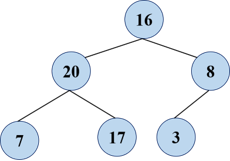
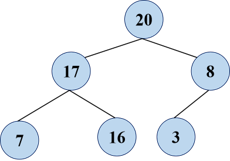
The number of the top and bottom of the reactor is exchanged.

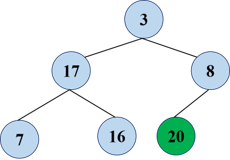
However, the heap may not meet the requirements at this time, and need to be readjusted again:

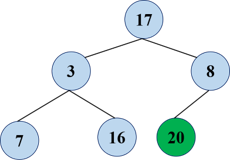
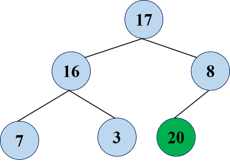
Repeat and swap the top and bottom of the heap (before, of course, the size of the heap was reduced by 1)

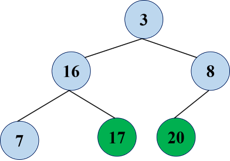
Another adjustment:

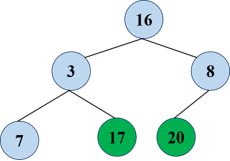
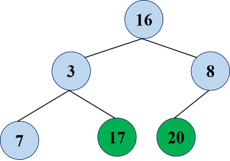
Repeat and swap the top and bottom of the heap (before, of course, the size of the heap has to be reduced by 1)

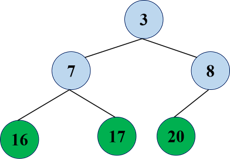
Readjustment:

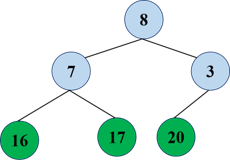
Re exchange:

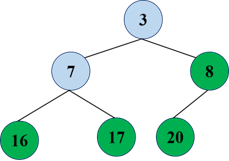
Readjustment:

Re exchange: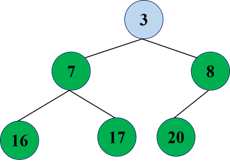

At this point, a heap sorting is completed and a minimum heap is finally obtained.

2. Python implementation

program

#Define a function for the parent node of a single node and its child size exchange
def initialMaxHeap(a,startIndex,endIndex):
    leftChildIndex=2*startIndex+1 #The parent node is I and the child on the left is 2*i+1
    #Judge whether the left child has the right child
    if leftChildIndex+1<=endIndex and a[leftChildIndex+1]>a[leftChildIndex]:
        leftChildIndex+=1       
    if a[leftChildIndex]>a[startIndex]:#When the left and right child values are greater than the value of the parent node, swap so that the maximum value of the binary tree is located on the parent node.
        temp=a[startIndex]
        a[startIndex]=a[leftChildIndex]

def myHeapSort(a):
    #a is the sequence to be sorted
    listLength=a.__len__()
    while True:
        if listLength==1:
            break;
        finalNodeHavingChild=(listLength)//2-1 #Find the parent node of the lowest layer
        #Down-to-up heap adjustment
        for i in range(finalNodeHavingChild,-1,-1):
            #print(a[i])
            initialMaxHeap(a,i,listLength-1)
        #After this adjustment, the definition of the maximum heap may not be satisfied and needs to be adjusted again from top to bottom.
        #Up-to-down heap adjustment
        for j in range(0,finalNodeHavingChild+1):
            #print(a[j])
            initialMaxHeap(a,j,listLength-1)
        #Change the number of top to bottom
        temp=a[0]
        a[0]=a[listLength-1]
        a[listLength-1]=temp
        #Reduce the number of heaps
        listLength-=1
    return a    

def generatingRandomNumber(sampleNumber,lower,upper):
    #sampleNumber: The length of the generated random sequence
    #Lower and upper are lower and upper bounds for generating random sequences, respectively
    #Finally, the function returns a random and disordered sequence a.
    import random
    a=[]
    aSize=a.__len__()
    while 1:
        aSize=a.__len__()
        if aSize>=sampleNumber:
            break
        else:
            temp=int(random.randint(lower,upper))
            a.append(temp)
    return a

if __name__=="__main__":
    a=generatingRandomNumber(20,1,100)
    print()
    print('the sequence before sorting is:\n')
    print(a)
    print()
    print('the sequence after sorting is:\n')
    print(myHeapSort(a))

The result is:

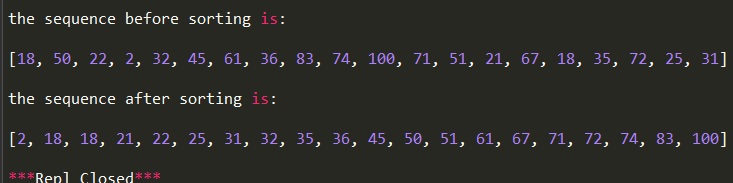
The result is correct!!!

Sorting dynamic graph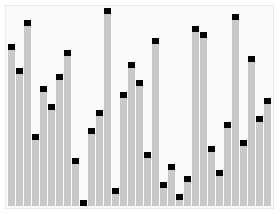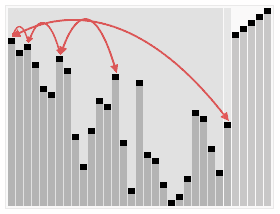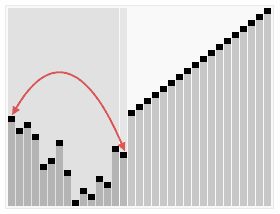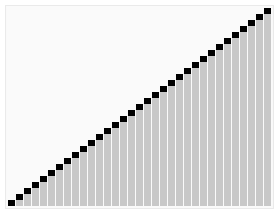

3. Time complexity analysis

In the process of building a heap (initializing a large top heap), a complete binary tree is constructed from the bottom and right non-terminal nodes, comparing it with its children and interchanging it as necessary. For each non-terminal node, in fact, at most two comparisons and one interchange operation are carried out, so the time complexity of the whole heap construction is O(n). About n2 2=n comparisons and n2 exchanges are needed.

In the formal sorting, the depth of the complete binary tree of N nodes is log2n +1, and the operation of adjusting n_1 to the large top heap is needed with n data. The time complexity of adjusting each time to the large top heap is O(log2n). Therefore, the time complexity of the reconstructed reactor can be approximated as O(nlog2n).