😶 🌫️ go official Programming Guide: https://pkg.go.dev/std
Go language official documents, learning notes are very complete, it is recommended to go to the official website to learn
😶 🌫️ My study notes: github: https://github.com/3293172751/golang-rearn
Blockchain Technology (also known as distributed ledger Technology) is an Internet database technology, which is characterized by decentralization, openness and transparency, allowing everyone to participate in database records
❤️💕💕 For blockchain technology, you can follow me and learn more blockchain technologies together. Blog http://nsddd.top
Learn to go in 45 days -- on the eighth day, golang sorting and searching
©️®️ Sorting and searching is a big direction. I'm going to combine the data structure with python, C/C + + as the auxiliary and Golang as the main line
sort
✍️ Sorting refers to the process of rearranging any sequence of data elements (or records) into an ordered sequence (increasing or decreasing) according to keywords, which is called sorting
Sorted classification
Sorting is divided into internal sorting and external sorting, as well as stable sorting and unstable sorting
1. Internal sorting
Internal sorting means that the whole sorting process is completely carried out in memory, including exchange sorting, selective sorting and plug-in sorting
2. External sorting
Due to the large amount of data, the memory cannot hold all the data. Sorting can be completed with the help of external storage devices, including * * (merge sorting method and direct merge sorting method)**
3. Stable sorting and unstable sorting
- Stable sorting: if the relative position of two equal numbers before and after sorting remains unchanged, the algorithm is stable
- Unstable sorting: if the relative position of two equal numbers changes before and after sorting, the algorithm is unstable
Discussion on the significance of stability
1. If you simply sort numbers, then stability will be meaningless.
2. If the sorting content is only a digital attribute of a complex object, then the stability will still be meaningless (the cost of the so-called exchange operation has been included in the cost of the algorithm. If you dislike this cost, you might as well change the algorithm?)
3. If the content to be sorted is multiple numeric attributes of a complex object, but its original initial order is meaningless, the stability will still be meaningless.
4. Unless the content to be sorted is multiple digital attributes of a complex object and its original initial order has meaning, we need to maintain the original sorting meaning on the basis of secondary sorting, and then we need to use a stable algorithm. For example, the content to be sorted is a group of objects originally sorted according to the price, and now we need to sort according to the sales volume, Using the stability algorithm, the objects with the same sales volume can still maintain the ranking display of price, and only those with different sales volume will be reordered. (of course, if the requirements do not need to maintain the initial sorting significance, it will still be meaningless to use the stability algorithm)
Exchange sort
✍️ The basic method of exchange sorting is to compare the keywords of the records to be sorted by pairwise. If there is a pair of data that does not meet the order requirements, exchange until all the positions are met
1. Bubble sort
Bubble Sort is also a simple and intuitive sorting algorithm. It repeatedly visits the sequence to be sorted, compares two elements at a time, and exchanges them if they are in the wrong order. The work of visiting the sequence is repeated until there is no need to exchange, that is, the sequence has been sorted. The name of this algorithm comes from the fact that smaller elements will slowly "float" to the top of the sequence through exchange.
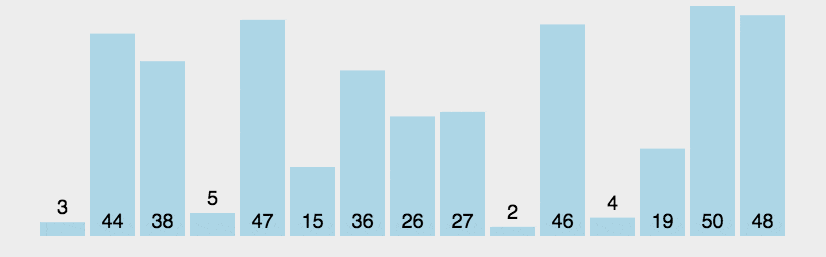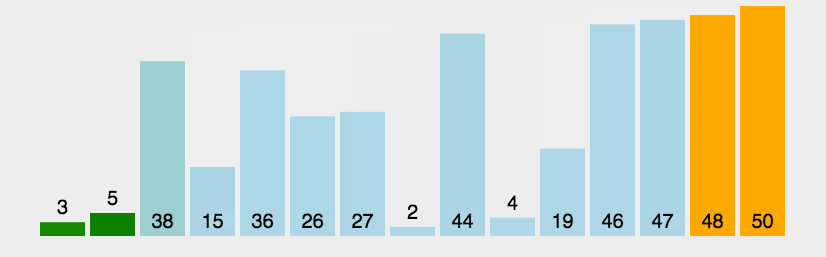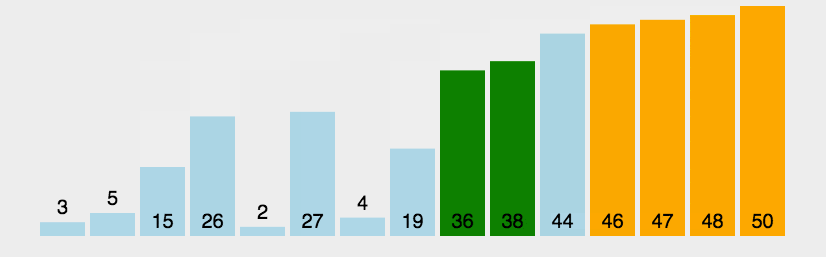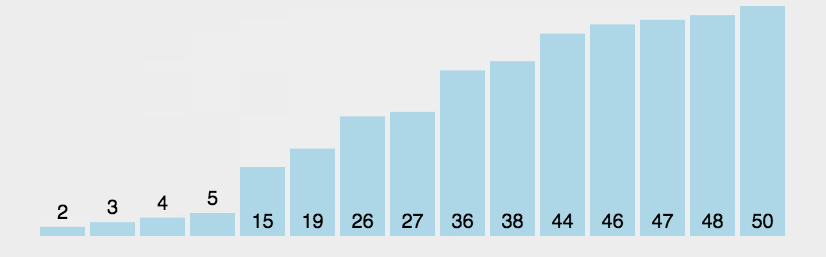
First, it is implemented in simple python
def bubbleSort(arr):
n = len(arr)
# Traverse all array elements
for i in range(n):
exchange = 0 #See if there is an exchange this time
# Last i elements are already in place
for j in range(0, n-i-1):
if arr[j] > arr[j+1] :
arr[j], arr[j+1] = arr[j+1], arr[j] //Direct exchange without intermediate variables
exchange = 1
if exchange == 0:
return arr
arr = [64, 34, 25, 12, 22, 11, 90]
bubbleSort(arr)
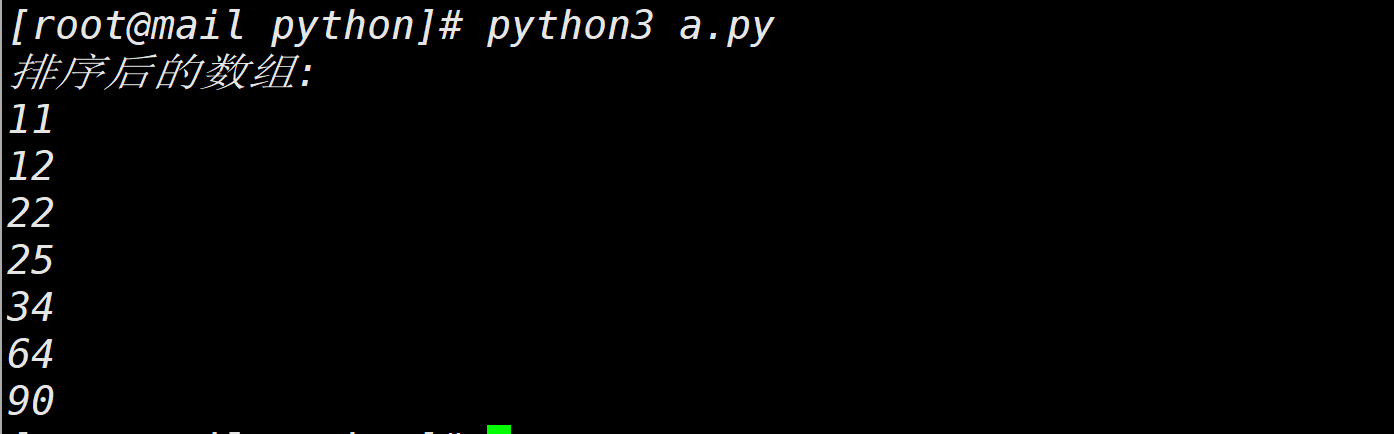
print ("Sorted array:")
for i in range(len(arr)):
print ("%d" %arr[i]),
compile:
def bubble_sort(array):
for i in range(1, len(array)):
a=0
for j in range(0, len(array)-i):
if array[j] > array[j+1]:
array[j], array[j+1] = array[j+1], array[j]
a=1
if a==0:
return array
return array
if __name__ == '__main__':
array = [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21]
print(bubble_sort(array))
compile:
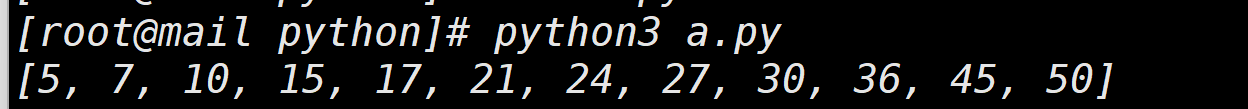
Thought:
An auxiliary is set. Once an operation without exchange is found, the program will be terminated immediately. At this time, the time complexity can be reduced
The following is Golang's bubble sorting algorithm:
package main
import (
"fmt"
"time"
)
func main() {
values := []int{4, 93, 84, 85, 80, 37, 81, 93, 27,12}
start := time.Now().UnixNano()
fmt.Println(values) //Prints the current slice
BubbleAsort(values) //Exchange function, values [i] > values [J] from small to large
BubbleZsort(values) //Exchange function, values [i] < values [J] from large to small
end := time.Now().UnixNano()
fmt.Println("Code execution time:",end-start)
}
func BubbleAsort(values []int) {
for i := 0; i < len(values)-1; i++ {
a := 0
for j := i+1; j < len(values); j++ {
if values[i]>values[j]{
values[i],values[j] = values[j],values[i] //Exchange directly like python
a = 1
}
}
if a ==0{
return
}
}
fmt.Println(values)
}
func BubbleZsort(values []int) {
a := 0
for i := 0; i < len(values)-1; i++ {
for j := i+1; j < len(values); j++ {
if values[i]<values[j]{
values[i],values[j] = values[j],values[i]
a = 1
}
}
if a ==0{
return
}
}
fmt.Println(values)
}
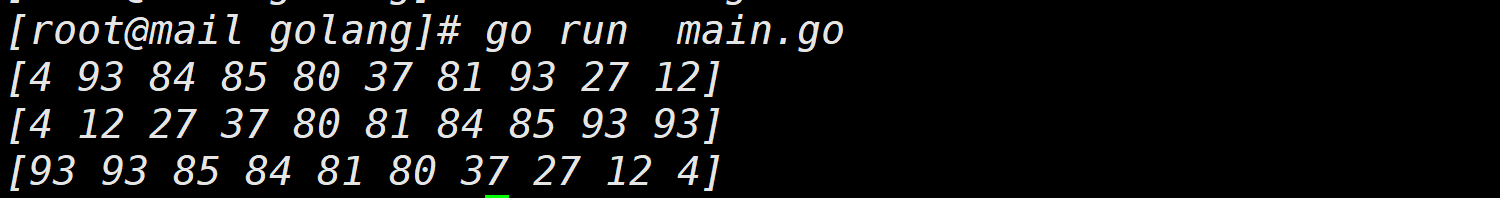
We can use Golang to count the code execution time with and without a
start := time.Now().UnixNano()
fmt.Println(values)
BubbleAsort(values)
BubbleZsort(values)
end := time.Now().UnixNano()
fmt.Println("Code execution time:",end-start)
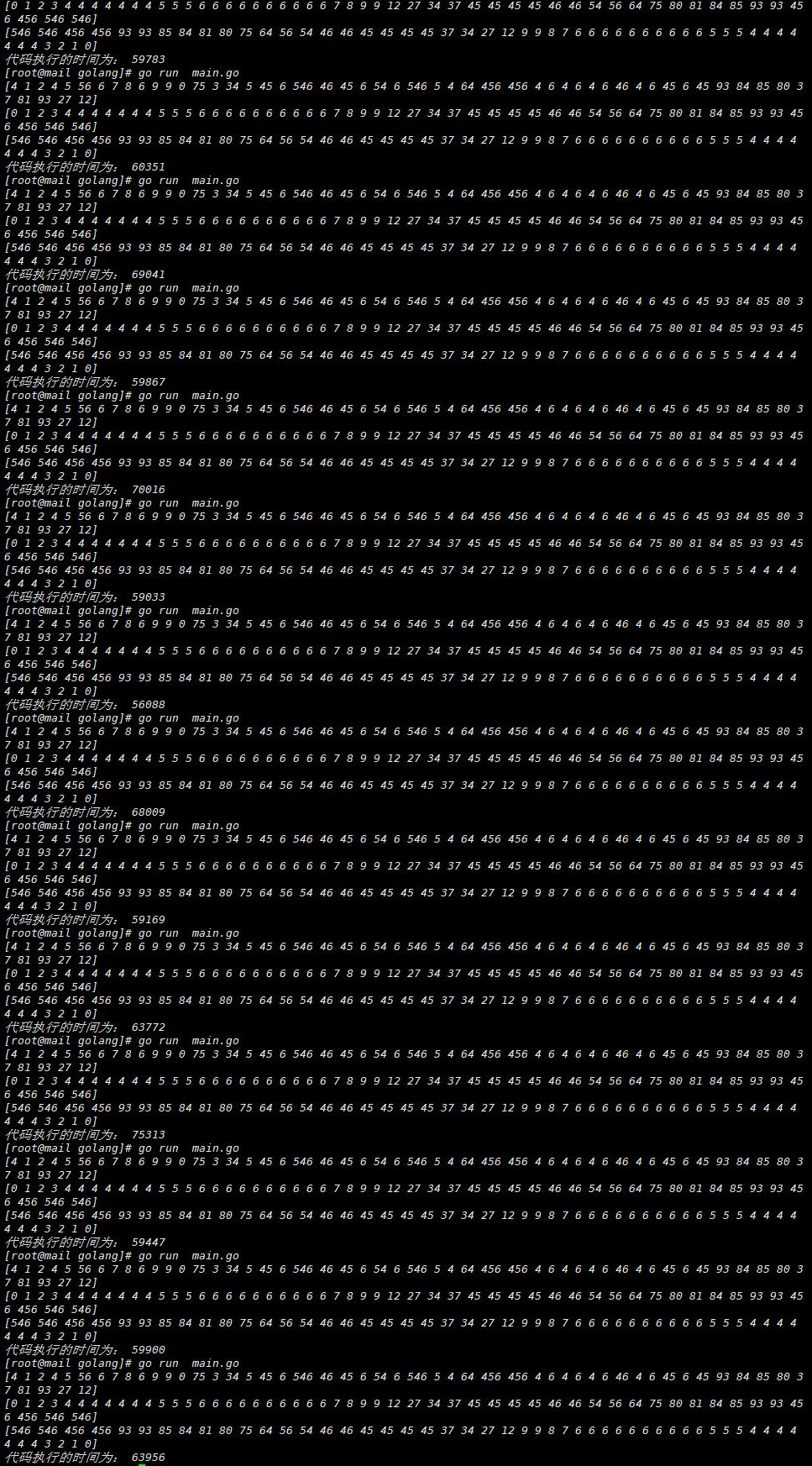
According to the big data analysis from top to bottom, it can be seen that the execution time of the code has indeed increased 😂😂😂
2. Quick sort
Quick sort is often used because its sorting efficiency is higher among several sorting methods called O(N*logN). In addition, the idea of quick sort - divide and conquer method is really practical. Therefore, many software companies like to take this test in written interviews, including well-known IT companies such as Tencent and Microsoft, as well as large-scale program tests such as soft test, Rapid sorting often appears in the postgraduate entrance examination.
Generally speaking, it is still difficult to write out quick sort directly from memory, because I have made a vernacular explanation for quick sort based on my own understanding, hoping to be helpful to everyone's understanding, so as to achieve quick sort and get it done quickly.
Quick sort is a partition exchange sort proposed by C.R.A.Hoare in 1962. It adopts a divide and conquer strategy, commonly known as divide and conquer method.
The basic idea of this method is:
-
1. First take a number from the sequence as the reference number.
-
2. In the partition process, all numbers larger than this number are placed on its right, and all numbers less than or equal to it are placed on its left.
-
3. Repeat the second step for the left and right intervals until there is only one number in each interval.
-
-
Although quick sort is called divide and conquer, the three words of divide and conquer obviously can not well summarize all the steps of quick sort. Therefore, my has further explained the quick sort: pit excavation and filling + divide and conquer method:
-
Let's take a look at the example first, and then give the definition below (it's best to summarize the definition in your own words, which will be helpful to the implementation code).
-
Taking an array as an example, take the first number of the interval as the benchmark number.
-
0 1 2 3 4 5 6 7 8 9 72 6 57 88 60 42 83 73 48 85 -
Initially, i = 0; j = 9; X = a[i] = 72
-
Since the number in a[0] has been saved to X, it can be understood as digging a hole in array a[0] and filling it with other data.
-
Start with J and move forward to find a number smaller than or equal to X. When j=8, meet the conditions, dig out a [8] and fill it into the previous pit a [0]. a[0]=a[8]; i++; Such a pit a [0] is solved, but a new pit a [8] is formed. What should we do? Easy, find the number to fill a[8] this hole. This time, find a number greater than x from I. When i=3, if it meets the conditions, dig out a[3] and fill it into the previous pit, a[8]=a[3]; j–;
-
The array becomes:
-
0 1 2 3 4 5 6 7 8 9 48 6 57 88 60 42 83 73 88 85 -
i = 3; j = 7; X=72
-
Repeat the above steps, first from the back to the front, and then from the front to the back.
-
Look forward from j, when j=5, meet the conditions, dig out a[5] and fill it into the previous pit, a[3] = a[5]; i++;
-
Start from i and look back. When i=5, exit because i==j.
-
At this time, i = j = 5, and a[5] is just the pit dug last time, so fill X in a[5].
-
The array becomes:
-
0 1 2 3 4 5 6 7 8 9 48 6 57 42 60 72 83 73 88 85 -
It can be seen that the numbers before a[5] are smaller than it, and the numbers after a[5] are larger than it. Therefore, repeat the above steps for the two sub intervals a[0... 4] and a[6... 9].
-
Sum up the number of excavation and filling:
-
- 1.i =L; j = R; Dig out the reference number to form the first pit a[i].
- 2. j – find the number smaller than it from back to front, dig out the number and fill it in the previous pit a[i].
- 3. i + + find a number larger than it from front to back. After finding it, dig out the number and fill it into the previous pit a[j].
- 4. Repeat steps 2 and 3 until i==j, and fill the benchmark number in a[i].
-
According to this summary, it is easy to implement the code of pit excavation and filling:
-
int AdjustArray(int s[], int l, int r) //Returns the position of the adjusted reference number
{
int i = l, j = r;
int x = s[l]; //s[l], or s[i], is the first pit
while (i < j)
{
// Find the number less than x from right to left to fill in s[i]
while(i < j && s[j] >= x)
j--;
if(i < j)
{
s[i] = s[j]; //When s[j] is filled into s[i], s[j] forms a new pit
i++;
}
// Find a number greater than or equal to x from left to right to fill in s[j]
while(i < j && s[i] < x)
i++;
if(i < j)
{
s[j] = s[i]; //When s[i] is filled into s[j], s[i] forms a new pit
j--;
}
}
//On exit, i equals j. Fill the hole with x.
s[i] = x;
return i;
}
Then write the code of divide and Conquer:
void quick_sort1(int s[], int l, int r)
{
if (l < r)
{
int i = AdjustArray(s, l, r);//Adjustment s[]t method of first excavation and filling
quick_sort1(s, l, i - 1); // Recursive call
quick_sort1(s, i + 1, r);
}
}
//Quick sort
void quick_sort(int s[], int l, int r)
{
if (l < r)
{
//Swap(s[l], s[(l + r) / 2]); // Swap the middle number with the first number. See Note 1
int i = l, j = r, x = s[l];
while (i < j)
{
while(i < j && s[j] >= x) // Find the first number less than x from right to left
j--;
if(i < j)
s[i++] = s[j];
while(i < j && s[i] < x) // Find the first number greater than or equal to x from left to right
i++;
if(i < j)
s[j--] = s[i];
}
s[i] = x;
quick_sort(s, l, i - 1); // Recursive call
quick_sort(s, i + 1, r);
}
}
Using python to implement
def partition(arr,low,high):
i = ( low-1 ) # Minimum element index
pivot = arr[high]
for j in range(low , high):
# The current element is less than or equal to pivot
if arr[j] <= pivot:
i = i+1
arr[i],arr[j] = arr[j],arr[i]
arr[i+1],arr[high] = arr[high],arr[i+1]
return ( i+1 )
# Arr [] -- > sort array
# Low -- > start index
# High -- > end index
# Quick sort function
def quickSort(arr,low,high):
if low < high:
pi = partition(arr,low,high)
quickSort(arr, low, pi-1)
quickSort(arr, pi+1, high)
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
quickSort(arr,0,n-1)
print ("Sorted array:")
for i in range(n):
print ("%d" %arr[i])
Execute the above code and the output result is:
Sorted array: 1 5 7 8 9 10
lookup
Linear search refers to checking each element in an array in a certain order until a specific value is found.
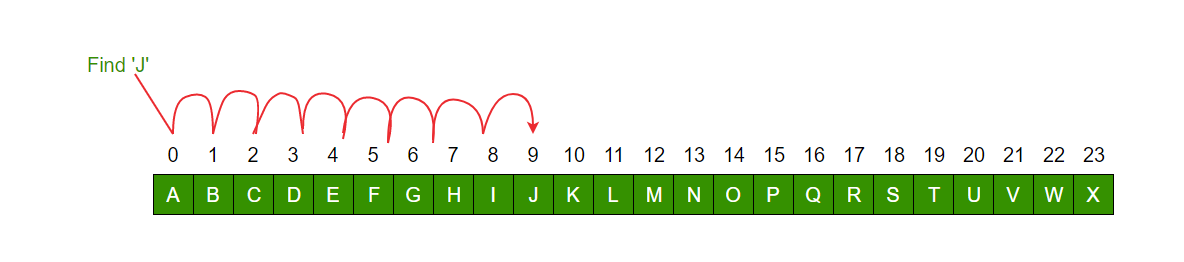
python instance
def search(arr, n, x):
for i in range (0, n):
if (arr[i] == x):
return i;
return -1;
# Find character D in array arr
arr = [ 'A', 'B', 'C', 'D', 'E' ];
x = 'D';
n = len(arr);
result = search(arr, n, x)
if(result == -1):
print("Element not in array")
else:
print("The index of the element in the array is", result);
Execute the above code and the output result is:
The index of the element in the array is 3
Python binary lookup
Binary search is a search algorithm to find a specific element in an ordered array. The search process starts from the middle element of the array. If the middle element is exactly the element to be found, the search process ends; If a specific element is greater than or less than the intermediate element, it is searched in the half of the array that is greater than or less than the intermediate element, and the comparison starts from the intermediate element as at the beginning. If the array is empty in a step, it means it cannot be found. Each comparison of this search algorithm reduces the search scope by half.
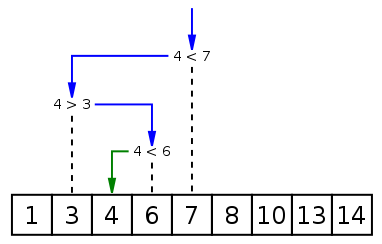
Example: recursion
# Returns the index of x in arr, or - 1 if it does not exist
def binarySearch (arr, l, r, x):
# Basic judgment
if r >= l:
mid = int(l + (r - l)/2)
# Middle position of element adjustment
if arr[mid] == x:
return mid
# If the element is smaller than the element in the middle, you only need to compare the element on the left
elif arr[mid] > x:
return binarySearch(arr, l, mid-1, x)
# If the element is larger than the element in the middle, you only need to compare the element on the right
else:
return binarySearch(arr, mid+1, r, x)
else:
# non-existent
return -1
# Test array
arr = [ 2, 3, 4, 10, 40 ]
x = 10
# function call
result = binarySearch(arr, 0, len(arr)-1, x)
if result != -1:
print ("The index of the element in the array is %d" % result )
else:
print ("Element not in array")
Execute the above code and the output result is:
The index of the element in the array is 3
Binary search of Golang
Binary search is based on an ordered array
package main
import (
"fmt"
)
func BinaryFind(arr *[6]int,lef int,rig int,find int){
//Arrays are passed by value and can be changed by using pointers
//Determine whether it is in the range of the array
if lef > rig{
fmt.Println("can't find") //Note that recursive calls conform to the inbound order, so
return
}
middle := (lef + rig) /2
if(*arr)[middle] > find{
//If it is greater than the number to find, you should look to the left
BinaryFind(arr,lef,middle - 1)
//Note that in this case, arr itself is a pointer, so no address character is required
}else if (*arr)[middle] < find{
BinaryFind(arr,middle+1,rig)
}else{
//Equality description found
fmt.Printf("All right, subscript%v \n",middle)
}
}
func main(){
arr := [6]int{1,2,3,4,5,6,7,8,9}
BinaryFind(&arr,0,len(arr)-1,4)
}
compile:
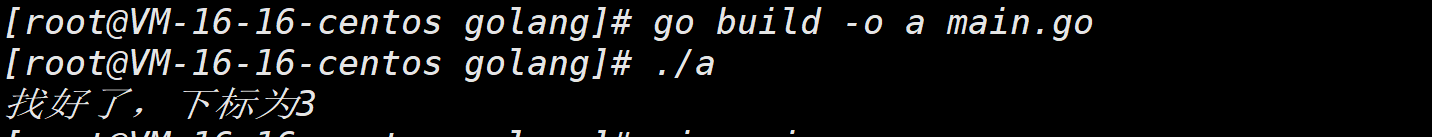
You can convert an array to a slice type without passing an address
rn
}
middle := (lef + rig) /2
if(*arr)[middle] > find{
//If it is greater than the number to find, you should look to the left
BinaryFind(arr,lef,middle - 1)
//Note that in this case, arr itself is a pointer, so no address character is required
}else if (*arr)[middle] < find{
BinaryFind(arr,middle+1,rig)
}else{
//Equality description found
fmt.Printf("found, subscript% v \n", middle)
}
}
func main(){
arr := [6]int{1,2,3,4,5,6,7,8,9}
BinaryFind(&arr,0,len(arr)-1,4)
}
compile: [External chain picture transfer...(img-hG7z2FJQ-1642076579101)] **You can convert an array to a slice type without passing an address**