Sorting concept

Before sorting, you should first introduce some concepts of sorting:

Sorting: it refers to the ascending or descending arrangement of a string of records according to the size of one or some keywords.
Stability: it is assumed that there are multiple records with the same keyword in the record sequence to be sorted. If they are sorted, the relative order of these records remains unchanged, that is, in the original sequence, r[i]=r[j], and r[i] is before r[j], while in the sorted sequence, r[i] is still before r[j], then this sorting algorithm is said to be stable; Otherwise, it is called unstable.
Internal sorting: sorting in which all data elements are placed in memory.
External sorting: there are too many data elements to be placed in memory at the same time. According to the requirements of the sorting process, the sorting of data cannot be moved between internal and external memory.

The scenario of sorting application is very common. For example, Taobao, jd.com and other e-commerce platforms will sort the babies you search, or make you hungry. Meituan will recommend nearby delicious food to you according to the high praise, which all use sorting.

Common sorting algorithms

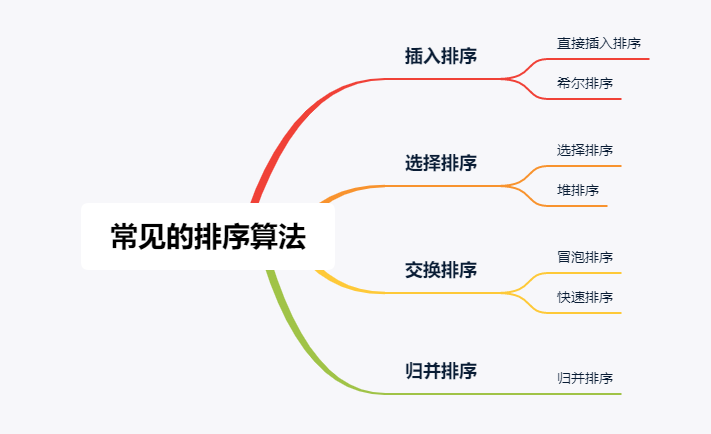
Implementation of sorting algorithm

Insert sort

Direct insert sort

First, let's look at a picture

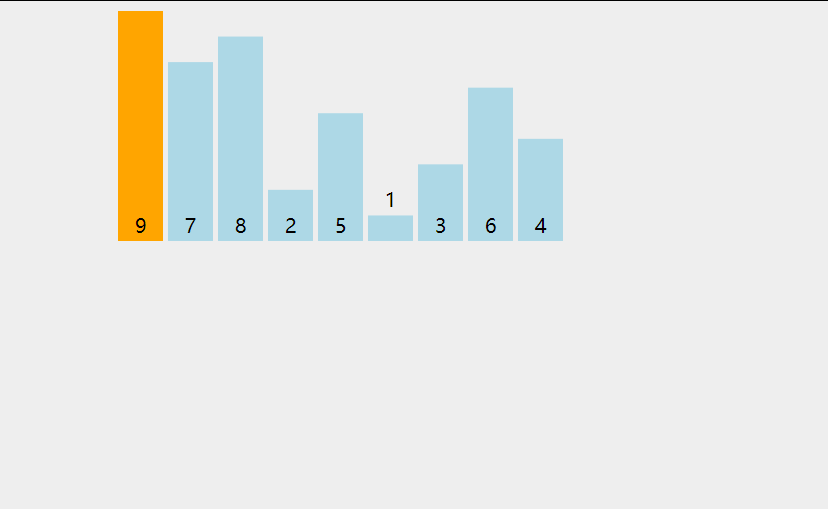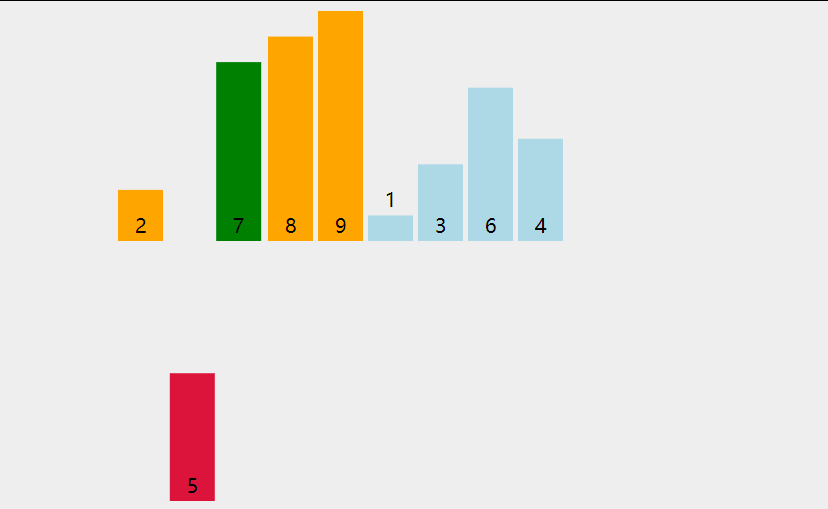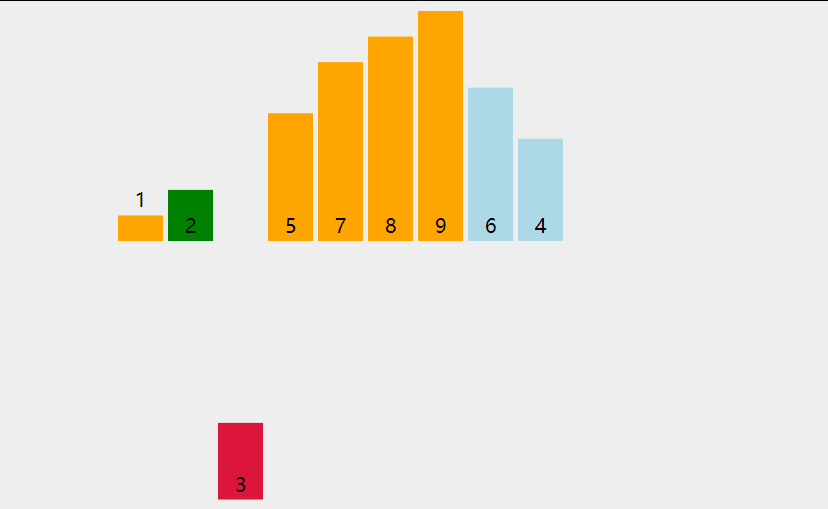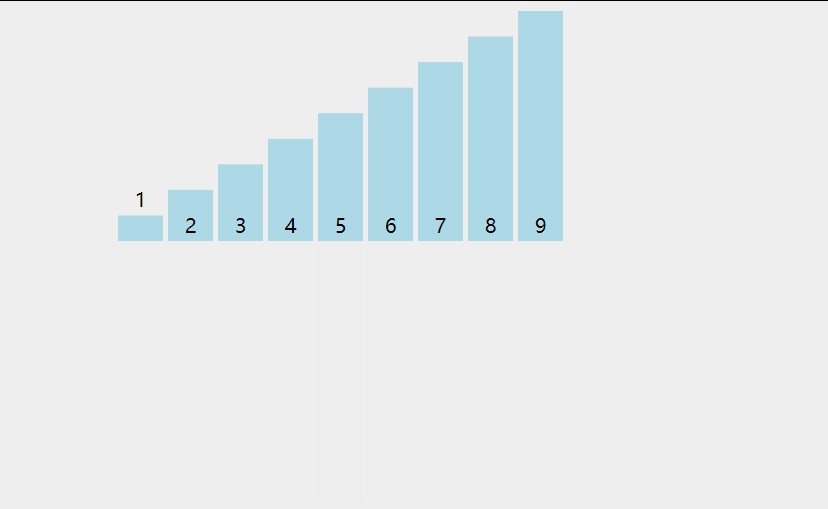
Analyze the steps of direct insertion sorting algorithm from this figure. First, the first number must be fixed. We think that the first number has been ordered. Then, starting from the first element, compare the value of arr[i] with the previously ordered value to find the appropriate position for insertion. If each comparison is not appropriate, move the element backward one bit.

Code implementation:

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void InsertSort(int* a, int n)
{
	int i = 0;
	for (i = 1; i < n; i++)
	{
		int num = a[i];
		int j = i - 1;
		while (j >= 0 && num < a[j])
		{
			Swap(&a[j], &a[j + 1]);
			j--;
		}
		a[j + 1] = num;
	}
}

Properties of direct insertion sort:

1. The closer the element set is to order, the higher the time efficiency of the direct insertion sorting algorithm
2. Time complexity: O(N^2)
3. Spatial complexity: O(1), which is a stable sorting algorithm
4. Stability: stable

Shell Sort

Hill ranking method is also known as reduced incremental method. The basic idea of hill sorting method is: first select an integer, divide all records in the file to be sorted into several groups, divide all records with gap distance into the same group, and sort the records in each group (insert sorting or other sorting). Then repeat the above grouping and sorting. When gap=1 is reached, all records are arranged in a unified group.

It can be said that Hill sort is to add the insertion sort of pre sort. When gap is not equal to 1, it is equivalent to a pre sort to make the sequence close to order. In this way, the efficiency of sub insertion sort is better.

As can be seen from the above figure, for an array, the gap of Hill sort for the first time is 5, and the elements with interval of 5 are inserted and sorted once; Then the gap becomes 2 and the insertion sort is performed again; Finally, gap is 1, that is, direct insertion sorting to make the whole array orderly.

Here's a little trick. If sorting groups by groups is too inefficient and you have to start from scratch after sorting a group, you can directly traverse the array and insert and sort for each element, because there will be no duplicate elements after gap grouping, so you can rest assured. In this way, you can pre sort a group divided by gap.

The code is as follows:

// Shell Sort 
void ShellSort(int* a, int n)
{
	//Given interval
	int gap = 5;
	while (gap)
	{
		//Due to the existence of gap, the number of traversals must be less than n-gap
		for (int i = 0; i < n - gap; i++)
		{
			//end every time it is i+gap, it avoids missing the last element
			int end = i + gap;
			//Terminates if the next element subscript is less than 0
			while (end - gap >= 0)
			{
				if (a[end] < a[end - gap])
					Swap(&a[end], &a[end - gap]);
				end -= gap;
			}
		}
		//gap divided by 2 each time  
		gap = gap / 2;
	}
}

Features of Hill sort:

1. Hill sort is an optimization of direct insertion sort.
2. When gap > 1, it is pre sorted, which aims to make the array closer to order. When gap == 1, the array is close to ordered, which will be very fast. In this way, the optimization effect can be achieved as a whole. We can compare the performance test after implementation.
3. The time complexity of Hill sort is not easy to calculate, so it needs to be deduced. The average time complexity deduced is O(N^1.3 - N^2)
4. Stability: unstable

Select sort

Selective sorting refers to selecting the smallest (or largest) element from the data elements to be sorted each time and storing it at the beginning of the sequence until all the data elements to be sorted are finished.

Direct selection sorting

1. Select the data element with the largest (smallest) key in the element set a[i] - a[n-1]
2. If it is not the last (first) element in the group, it is exchanged with the last (first) element in the group
3. In the remaining a[i] – a[n-2] (a[i+1] – a[n-1]) set, repeat the above steps until there is 1 element left in the set

Of course, we can choose the largest or the smallest at one time, or choose the largest and the smallest at the same time. There is no difference in the time complexity between the two.

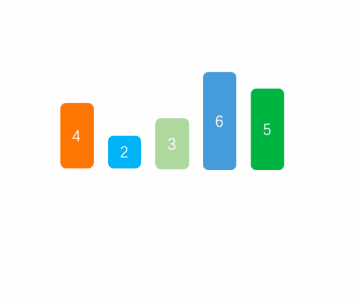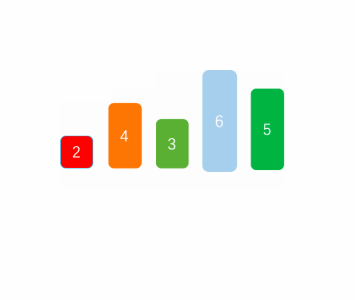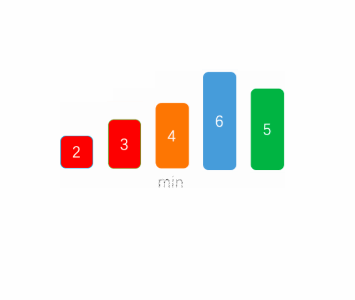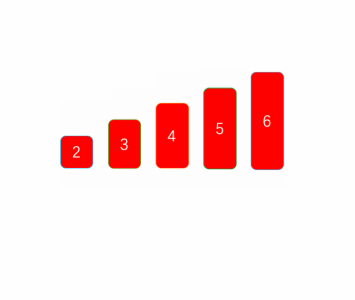
As can be seen from the above figure, select the smallest one at each time and put it at the first position of the sequence, then do not regard the smallest element found as the one in the next queue, and then continue to find the smallest of the remaining sequences, and so on until there is one element left.

The code is as follows:

// Select sort
void SelectSort(int* a, int n)
{
	int left = 0, right = n;
	while (left < right)
	{
		//Find the maximum and minimum value of the current sequence each time
		int min = left, max = left;
		for (int i = left; i < right; i++)
		{
			if (a[i] < a[min])
				min = i;
			if (a[i] > a[max])
				max = i;
		}
		//Place the maximum and minimum values at the beginning and end of the current sequence respectively
		Swap(&a[left], &a[min]);
		//If the maximum value is at the minimum value to be placed, it needs to be handled
		//After exchange, the original maximum value is at the original minimum value
		if (max == left)
			max = min;
		Swap(&a[right - 1], &a[max]);
		left++;
		right--;
	}
}

Directly select the characteristics of sorting:

1. It is very easy to understand the direct selection sorting thinking, but the efficiency is not very good. Rarely used in practice
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: unstable

Heap sort

Heap sort is a sort algorithm designed by using the data structure of heap. It is a kind of selective sort. It selects data through the heap. It should be noted that large piles should be built in ascending order and small piles should be built in descending order. Heap sorting is described in detail in my previous blog. Here is a picture for you to understand.

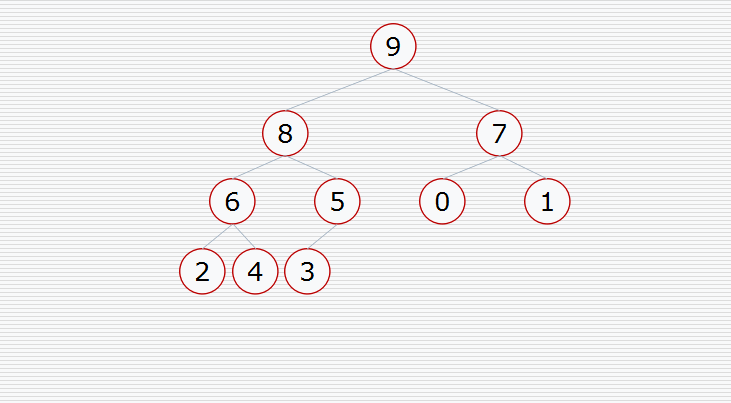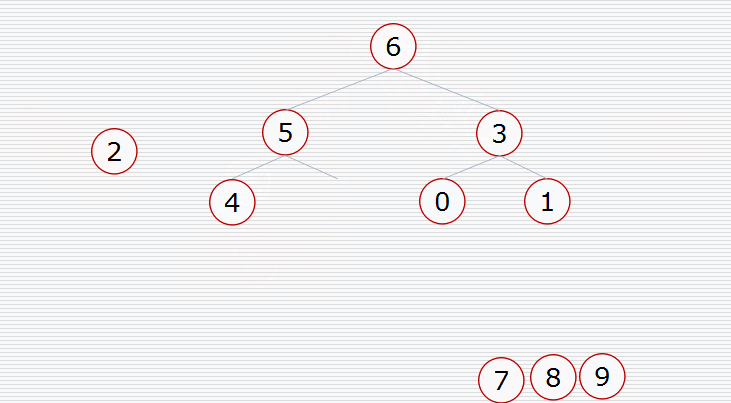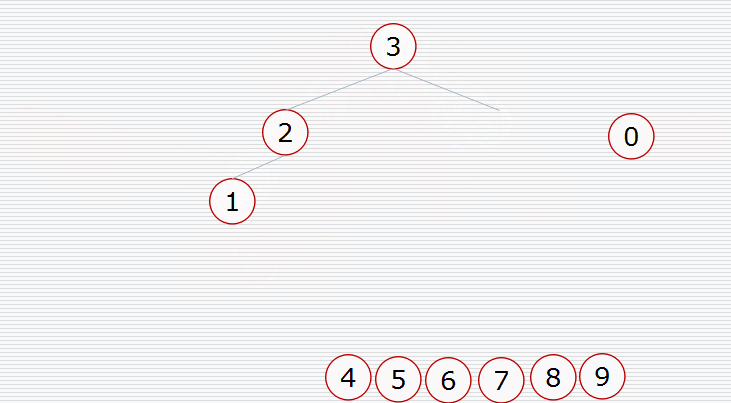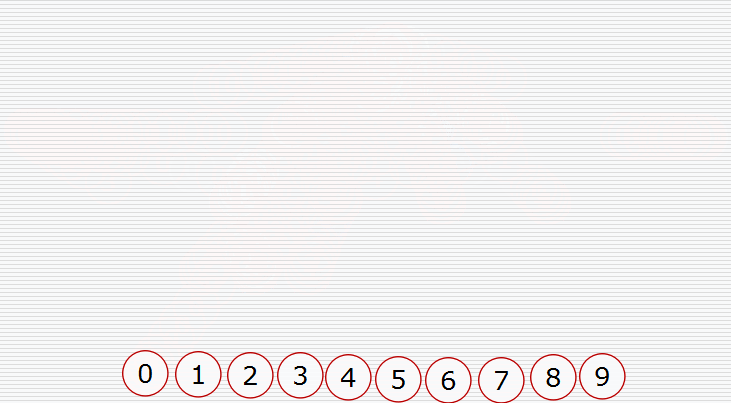
As can be seen from the above figure, if you want to arrange in ascending order, you need to build a large pile. If you build a small pile, you will destroy the structure of the tree (the same is true for arranging in descending order). After a heap is built, the maximum number must be at the top of the heap. Then take it down and exchange it with the last element of the heap. The maximum number is not counted as the element of the heap in the subsequent sorting. Putting the last element on the top of the heap may not meet the characteristics of a lot of heap. Then, after the exchange, make a downward adjustment to make the heap still maintain the characteristics of large root heap. Repeat until all numbers are sorted.

The code is as follows:

// Heap sort
void AdjustDwon(int* a, int n, int root)
{
	//Suppose a large root pile is built
	int parent = root;
	int child = 2 * parent + 1;//Suppose the left child is exchanged, and judge later
	//Each exchange must be the largest
	//Compare the left child with the right child. If the right child is older, change the child to the right child
	if (child + 1 < n && a[child] < a[child + 1])
		child++;
	while (child < n && a[parent] < a[child])
	{
		if (child + 1 < n && a[child] < a[child + 1])
			child++;
		Swap(&a[parent], &a[child]);
		parent = child;
		child = 2 * parent + 1;
	}
}
void HeapSort(int* a, int n)
{
	int i = 0;
	//Heap sorting requires building a heap first
	//Build a large pile in ascending order and a small pile in descending order
	for (i = n - 1; i >= 0; --i)
	{
		AdjustDwon(a, n, i);
	}
	//sort
	for (i = n - 1; i > 0; --i)
	{
		//Swap elements at the head and tail of the heap
		Swap(&a[i], &a[0]);
		//Adjust the stack head element downward
		//After the exchange, the largest element is not counted in the heap, so the length of the heap should be reduced by one
		AdjustDwon(a, --n, 0);
	}
}

Characteristics of heap sorting:

1. Heap sorting uses heap to select numbers, which is much more efficient.
2. Time complexity: O(N*logN)
3. Space complexity: O(1)
4. Stability: unstable

Exchange sort

Exchange sorting refers to exchanging the positions of the two records in the sequence according to the comparison results of the key values of the two records in the sequence.

The characteristics of exchange sorting are: move the records with larger key values to the tail of the sequence, and the records with smaller key values to the front of the sequence.

Bubble sorting

Bubble sorting refers to repeatedly visiting the element column to be sorted, comparing two adjacent elements in turn, and exchanging them if the order is wrong.

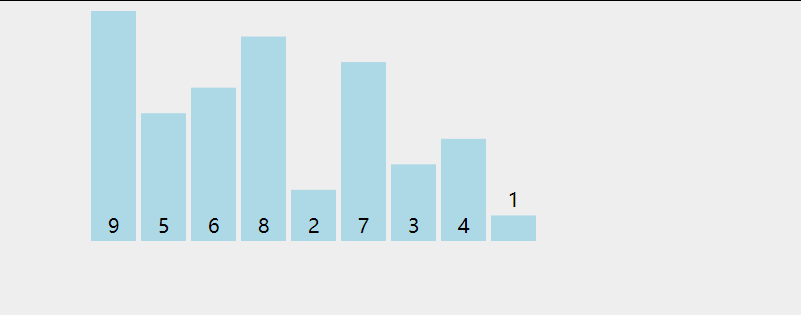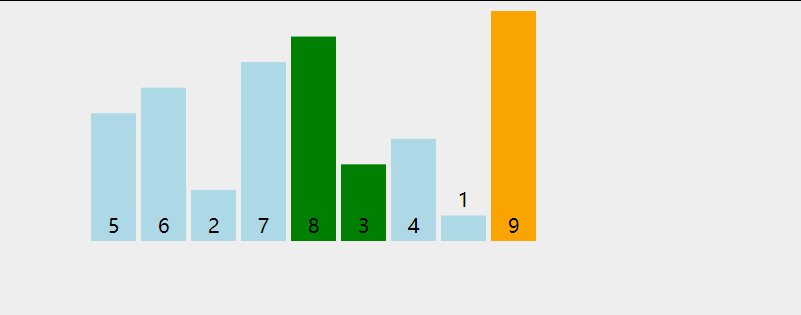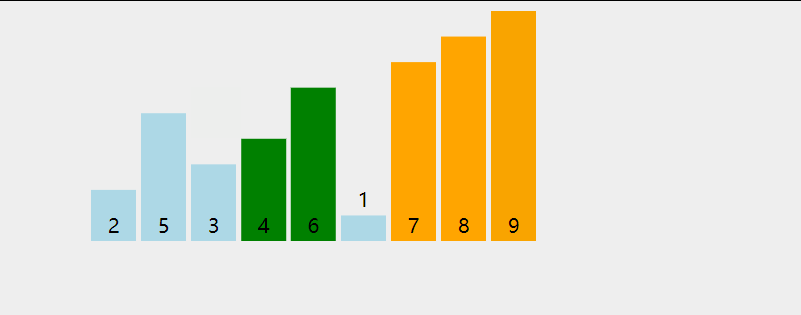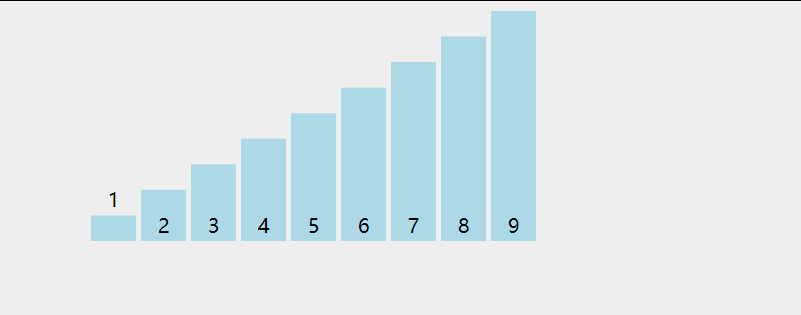
In each trip, the two elements in the wrong order are exchanged until they reach the end of the sequence. Then, the last element is not counted in the queue, and the next sorting is continued, and so on, until there are no exchangeable elements.

The code is as follows:

//Bubble sorting

void BubbleSort(int* a, int n)
{
	int i, j;
	int flag = 0;//As the identification of whether there are elements exchanged in the trip
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n - i - 1; j++)
		{
			flag = 1;
			if (a[j] > a[j + 1])
				Swap(&a[j], &a[j + 1]);
		}
		//If the flag is 0, it indicates that the sequence has been ordered
		if (flag == 0)
			break;
	}
}

Characteristics of bubble sorting:

1. Bubble sort is a sort that is very easy to understand
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: stable

Quick sort

Quick sort refers to dividing the data to be sorted into two independent parts through one-time sorting. All the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method.

(1) Hoare method

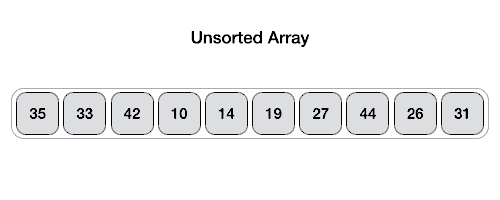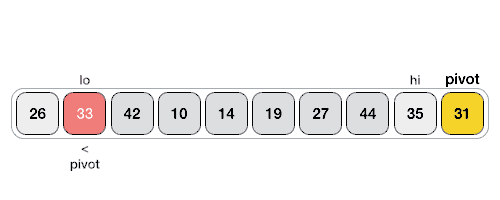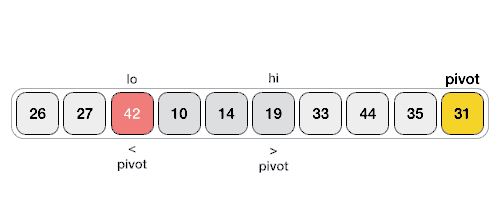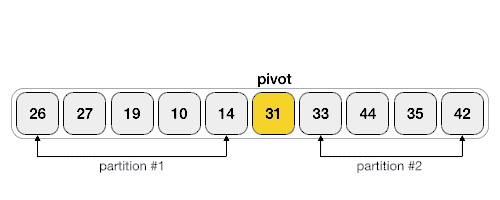
The figure above shows a quick sorting trip of Hoare method. The benchmark value can be the leftmost value or the rightmost value. This is not specified. Given two pointers, the left pointer lo and the right pointer Hi, if the reference value is on the left, let hi go first; If the reference value is on the right, let Lo go first. Assuming that the reference value is on the right, let the left pointer Lo go first to find a number larger than the reference value, and then the right pointer go again to find a number smaller than the reference value. Then exchange the elements of the two pointers, and so on, until the left and right pointers meet, and finally exchange the elements at the meeting position with the reference value. In this way, the left side of the benchmark value is the number smaller than the benchmark value, and the right side is the number larger than the benchmark value. In this way, the sorting is completed. At this time, the whole sequence is divided into left and right parts, and then continue to sort these two parts. Until all the elements are sorted.

The code is as follows:

//Hoare method --- one trip sorting
int PartSort_Hoare(int* a, int left, int right)
{
		int pivot = left;//The reference value is set to the left value
		while (left < right)
		{
			//Go first on the right and find one smaller than the benchmark value
			while (right > left && a[right] > a[pivot])
				right--;
			//Go to the left and find one larger than the benchmark value
			while (left < right && a[left] <= a[pivot])
				left++;
			//Exchange elements corresponding to left and right pointers
			if (left < right)
			Swap(&a[left], &a[right]);
		}

		//Finally, exchange the reference value and the value of the meeting point
		Swap(&a[pivot], &a[left]);

		return left;
}

(2) Excavation method

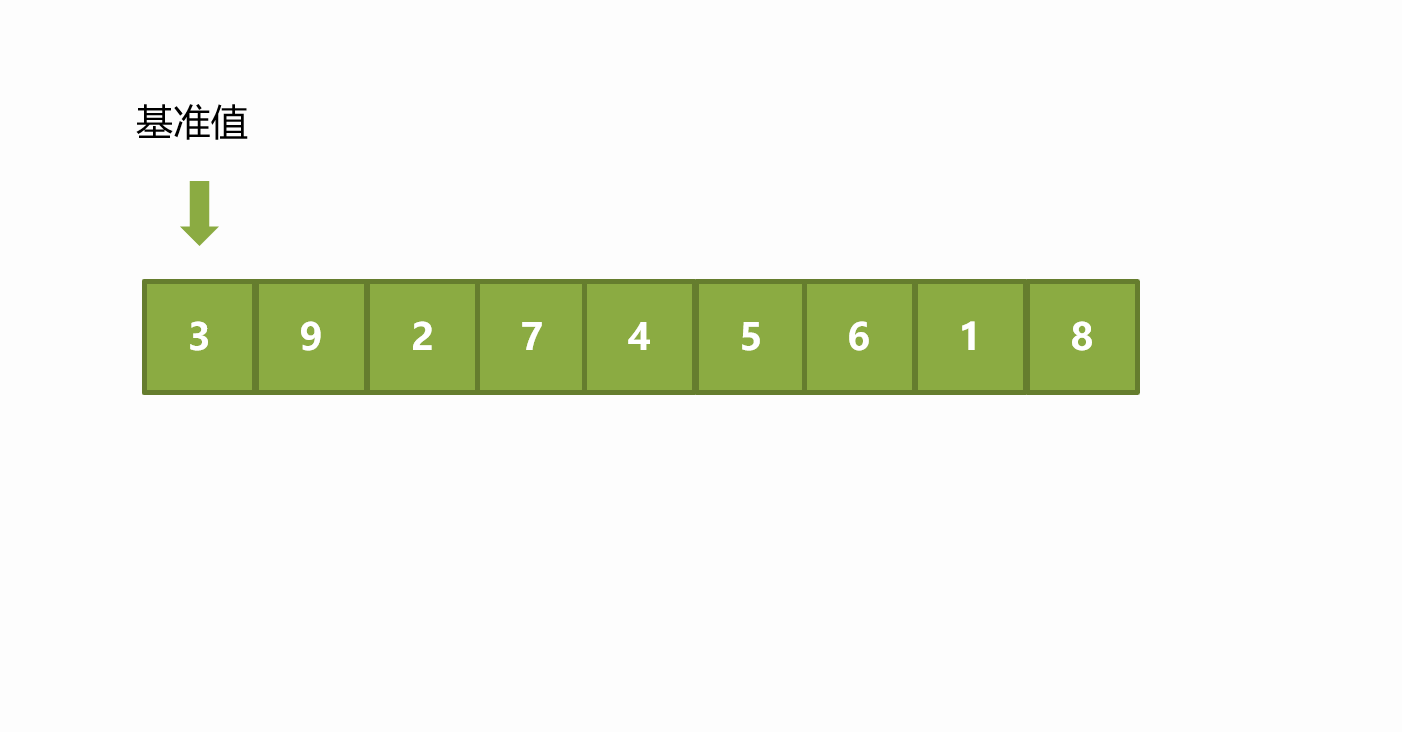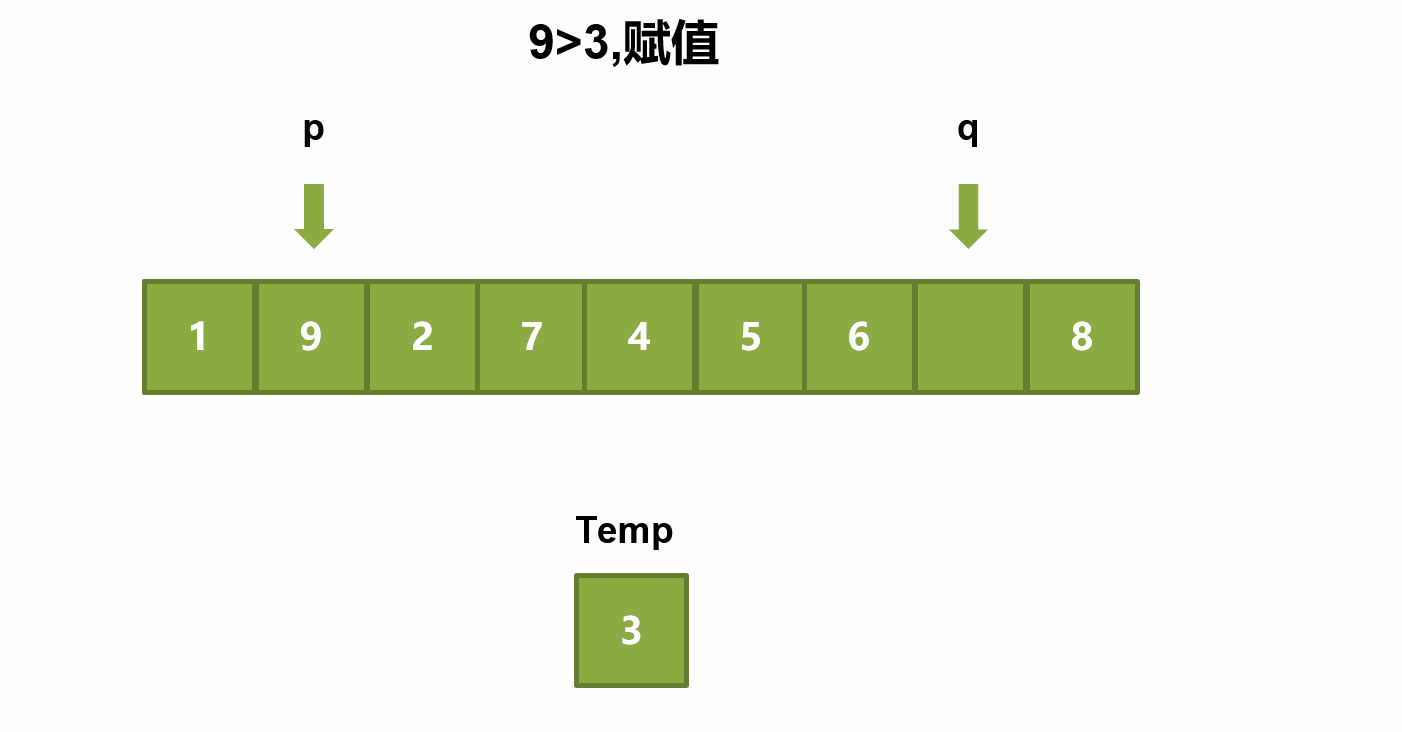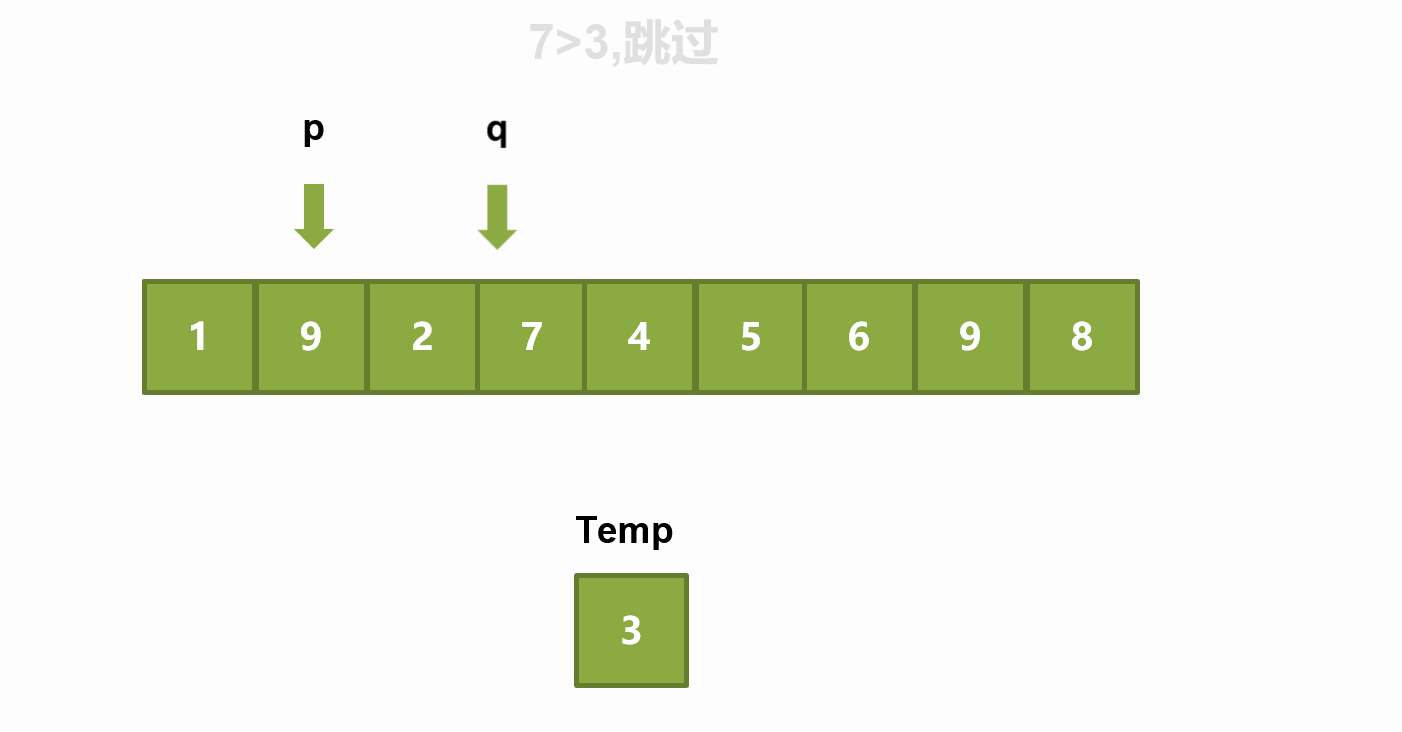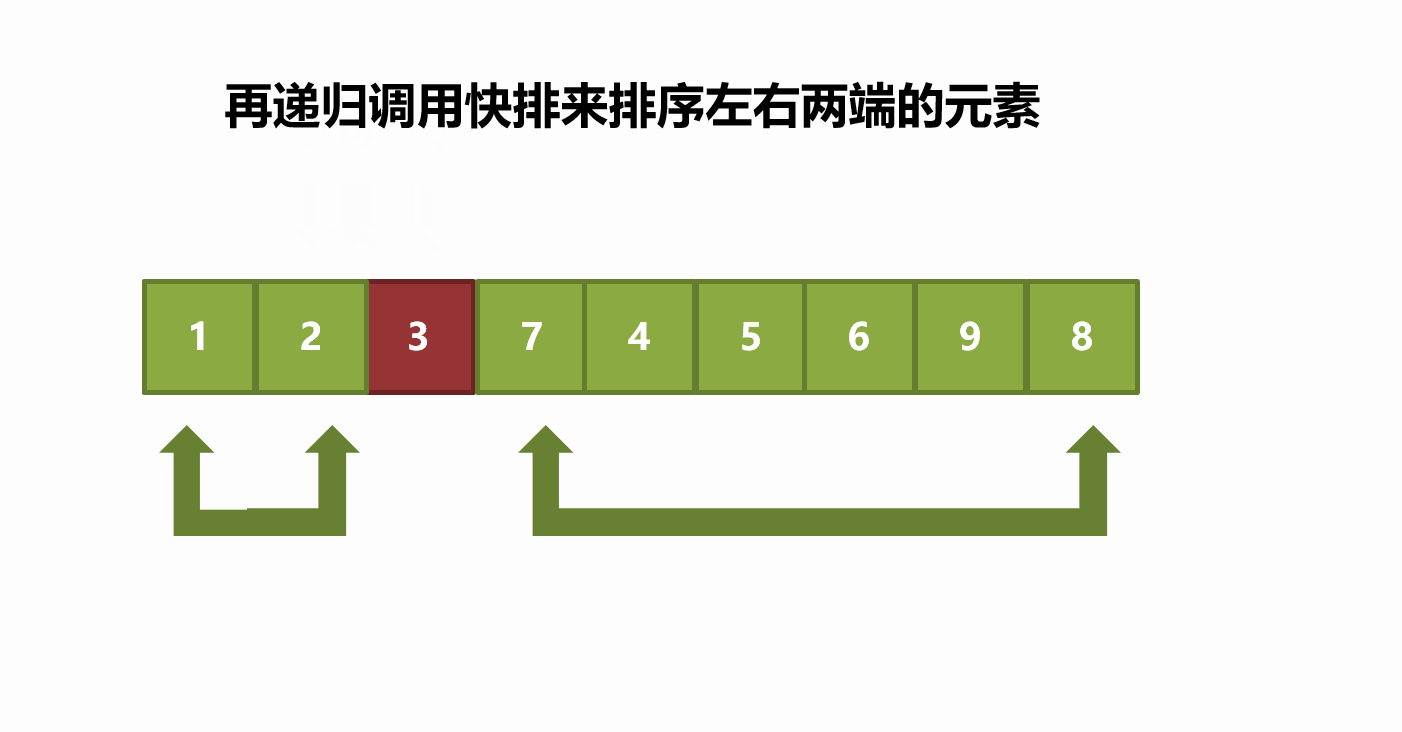
The basic idea of the pit digging method is similar to that of the Hoare method. The difference is that the Hoare method exchanges elements in the process of sorting in one trip, while the pit digging method takes out the elements at the benchmark value and regards the position corresponding to the benchmark value as a pit, that is, an empty position. Assuming that the reference value is the leftmost element, let the right pointer go first, find the element smaller than the reference value and put it in the empty pit. At this time, the corresponding position of the right pointer becomes a pit, and then move the left pointer to find the element larger than the reference value and put it in the pit, taking the corresponding position of the left pointer as a pit. And so on, until the left and right pointers meet, put the reference value in the last pit. At this time, the left and right of the benchmark values continue to be sorted according to this method until all sorting is completed.

The code is as follows:

//Pit digging method -- one trip sorting
int PartSort_Potholing(int* a, int left, int right)
{
	int space = left;//Representation pit
	int pivot = a[left];//The reference value is the leftmost
	while (left < right)
	{
		//Go first on the right, find one smaller than the reference value and put it in the pit
		while (right > left && a[right] >= pivot)
			right--;
		if (left < right)
		{
			a[space] = a[right];
			space = right;
		}
		//Go to the left again, find one larger than the reference value and put it in the pit
		while (left < right && a[left] <= pivot)
			left++;
		//Put the elements of the meeting point into the pit, and then the meeting point is a new pit
		if (left < right)
		{
			a[space] = a[left];
			space = left;
		}
	}
	//Finally, put the reference value in the empty pit
	a[space] = pivot;
	return space;
}

Front and back pointer method

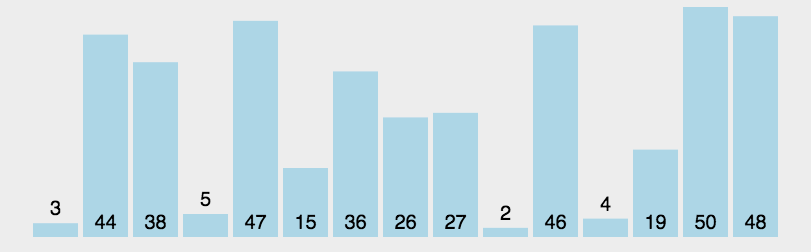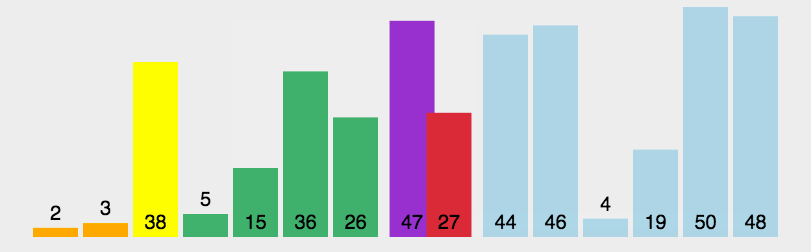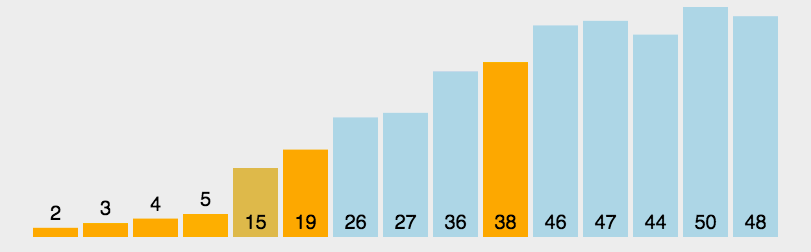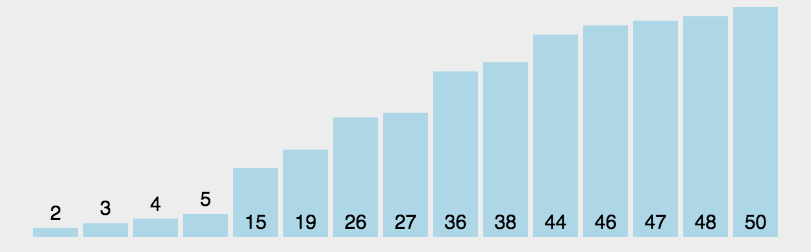
The front and back pointer method is slightly different from the first two methods. Through the first and second pointers prev and cur, cur first looks for the value smaller than the reference value, and then prev moves back one bit. If it is not equal to the subscript of cur, it will be exchanged. And so on, until cur comes to the end of the sequence, and then exchange prev and reference value, and the sorting is finished. Then, the left and right parts of the reference value are sorted in this way until all elements are sorted.

The code is as follows:

//Front and back pointer method -- one pass sorting
int PartSort_DoublrPtr(int*a, int left, int right)
{
	int pivot = left;
	int prev = left, cur = left + 1;
	while (cur <= right)
	{
		//cur first find the one smaller than the benchmark value
		while (cur <= right && a[cur] >= a[pivot])
			cur++;
		//If cur goes to the end of the sequence at this time, it means that there is no smaller number on the left of the benchmark value, and sorting is not required
		if (cur > right)
			break;
		//After finding it, prev + + will exchange if it is not equal to cur
		prev++;
		if (prev != cur)
		{
			Swap(&a[prev], &a[cur]);
		}
		//If cur is not added here, it will lead to dead cycle
		cur++;
	}
	Swap(&a[prev], &a[pivot]);
	return prev;
}

Fast scheduling can be realized by recursion or non recursion. Here we will talk about the recursive version first.
After each sorting, a middle coordinate will be found. The whole sequence is divided into two parts by the middle coordinate. In this way, it looks like the structure of binary tree, so we can complete the sorting by recursion.
Recursion needs to meet two conditions:
(1) The termination condition is that the left pointer is greater than or equal to the right pointer, because as long as the left pointer is less than the right pointer, it means that there are at least two elements in the sequence and sorting can continue; An element does not need to be sorted.
(2) After each sorting, the middle coordinate will divide the sequence into two halves. In this way, the continuous segmentation will slowly approach the end condition.

The code is as follows:

void _QuickSort(int* a, int left, int right)
{
	//If left is greater than or equal to right, it means that sorting is not required and you can return directly
	if (left >= right)
	{
		return;
	}
	//Otherwise, sort the left and right respectively
	else
	{
		//First, sort the sequence to find the benchmark
		int base = PartSort_DoublrPtr(a, left, right);
		//Sort the left and right parts respectively
		_QuickSort(a, left, base - 1);
		_QuickSort(a, base + 1, right);
	}
}

void QuickSort(int* a, int n)
{
	//Go in and call the quick row sub function directly
	_QuickSort(a, 0, n - 1);
}

Optimization of fast exhaust

I don't know if you have found it. If a sequence is arranged in descending order and we want to arrange in ascending order, the time complexity of using fast sorting is O(N^2), and the efficiency is very low. In this way, there may be no difference between using fast sorting and other sorting. However, fast sorting is a very common sort in sorting, so we need to make an optimization scheme for this situation.

There are two optimized schemes:

1. Triple median method

Taking the middle of three numbers refers to comparing the leftmost, rightmost and middle numbers, and selecting the middle value as the benchmark value. In this way, the problem of low efficiency in extreme cases can be avoided.

//Triple median method
int GetMiddle(int* a, int left, int right)
{
	int mid = (left + right) >> 1;
	//If the middle value is greater than the left value
	if (a[mid] > a[left])
	{
		//Compare the middle value with the right value. If the right value is large, the middle value is the reference value
		if (a[right] > a[mid])
			return mid;
		//If the middle value is greater than the right value, the middle value is the largest. Compare the size of the left value and the right value
		//If the right value is greater than the left value, the left value is the reference value
		else if (a[left] < a[right])
			return right;
		//If the left value is greater than the right value, the right value is the reference value
		else
			return left;
	}
	//If the middle value is less than or equal to the left value
	else
	{
		//If the intermediate value is greater than the right value, the intermediate value is the reference value
		if (a[mid] > a[right])
			return mid;
		//If the middle value is less than the right value and the middle value is the smallest, compare the size of the left value and the right value
		//If the right value is less than the left value, the right value is the reference value
		else if (a[right] < a[left])
			return right;
		//If the left value is less than the right value, the left value is the reference value
		else
			return left;
	}
}

2. Inter cell optimization

After recursion to a given cell, instead of using fast sorting, insert sorting is used. That is to say, in a small interval, this part can be sorted first, and then quickly sorted. The efficiency will be much higher.

void _QuickSort(int* a, int left, int right)
{
	//If left is greater than or equal to right, it means that sorting is not required and you can return directly
	if (left >= right)
	{
		return;
	}
	//Otherwise, sort the left and right respectively
	else
	{
		//Use fast platoon outside the cell
		if (right - left > MAX_LENGTH_INSERT_SORT)
		{
			//First, sort the sequence to find the benchmark
			int base = PartSort_DoublrPtr(a, left, right);
			_QuickSort(a, left, base - 1);
			_QuickSort(a, base + 1, right);
		}
		//Inter cell insertion sorting
		else
		{
			_InsertSort(a, left, right);
		}
	}
}

Fast non recursive

Fast scheduling can be implemented recursively or non recursively.
Non recursive implementation requires stack, which simulates the process of recursion. Each time, put the left and right subscripts that need to be partially sorted into the stack, and then after sorting for a period, take the left and right subscripts out of the stack, and update the left and right subscripts in the stack until the stack is empty.

//Fast non recursive
void QuickSort_NonR(int* a, int left, int right)
{
	Stack s;
	StackInit(&s);

	//Put the first left and right subscripts on the stack
	StackPush(&s, left);
	StackPush(&s, right);

	//loop
	//If the stack is not empty, it indicates that there are still sequences to be sorted
	while (!StackEmpty(&s))
	{
		//The left pointer enters the stack first, and the left pointer enters later
		//The right pointer comes out first, and the left pointer comes out later
		int end = StackTop(&s);
		StackPop(&s);
		int begin = StackTop(&s);
		StackPop(&s);
		//Partial sorting according to left and right pointers
		int base = PartSort_Hoare(a, begin, end);
		//If the left pointer is smaller than the right pointer, put the subscript on the stack
		if (begin < base - 1)
		{
			StackPush(&s, begin);
			StackPush(&s, base - 1);
		}

		if (end > base + 1)
		{
			StackPush(&s, base + 1);
			StackPush(&s, end);
		}
	}

	StackDestory(&s);
}

Quick sort features:

1. The overall comprehensive performance and usage scenarios of quick sort are relatively good
2. Time complexity: O(N*logN)
3. Space complexity: O(logN)
4. Stability: unstable

Merge sort

Merge sort is a very typical application of divide and conquer. Merge the ordered subsequences to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered.

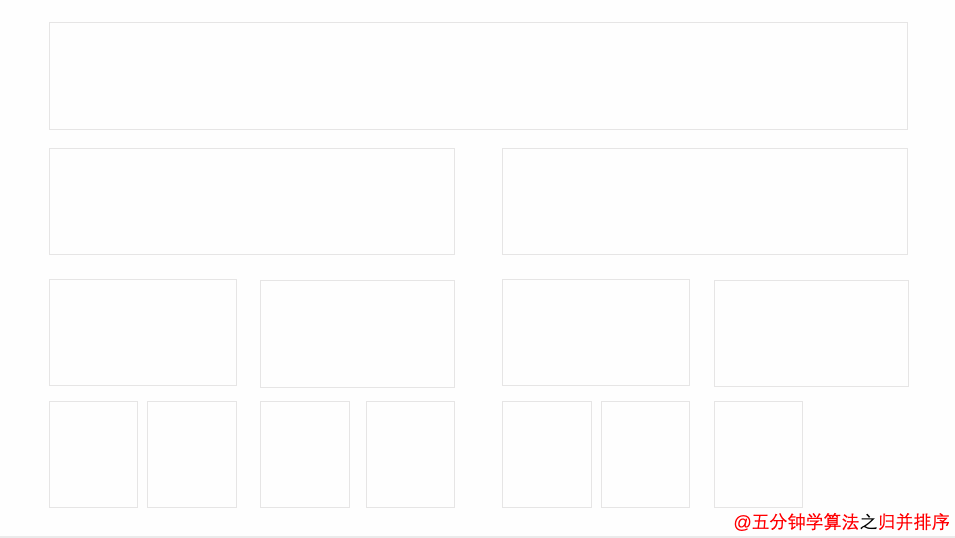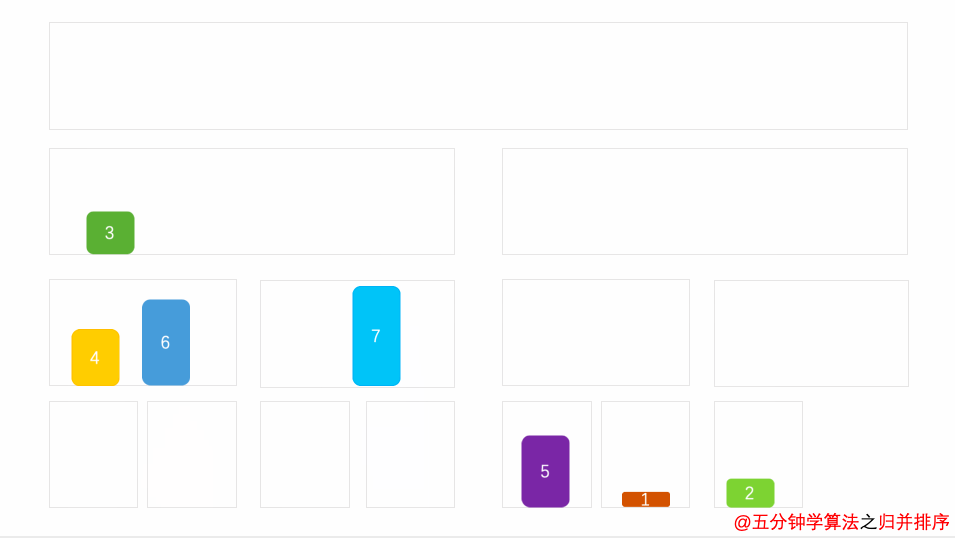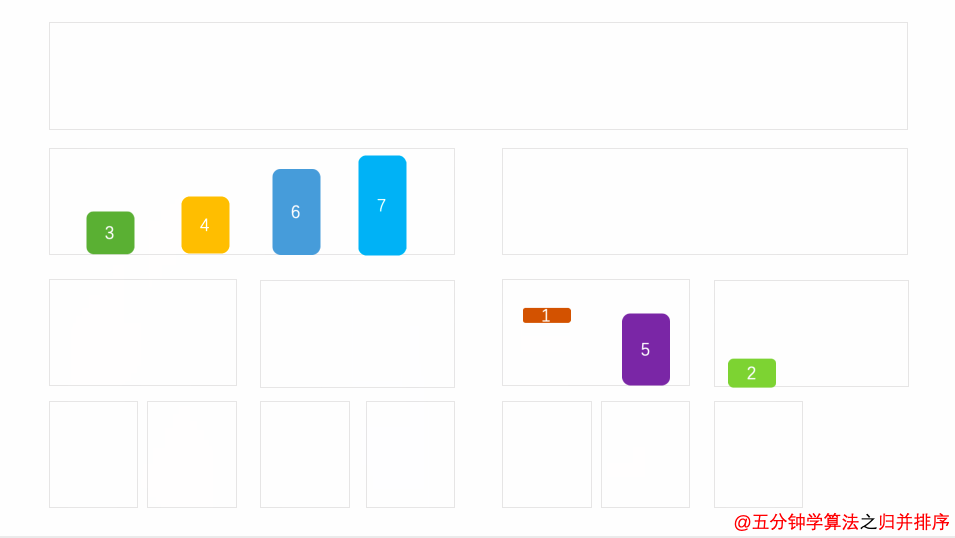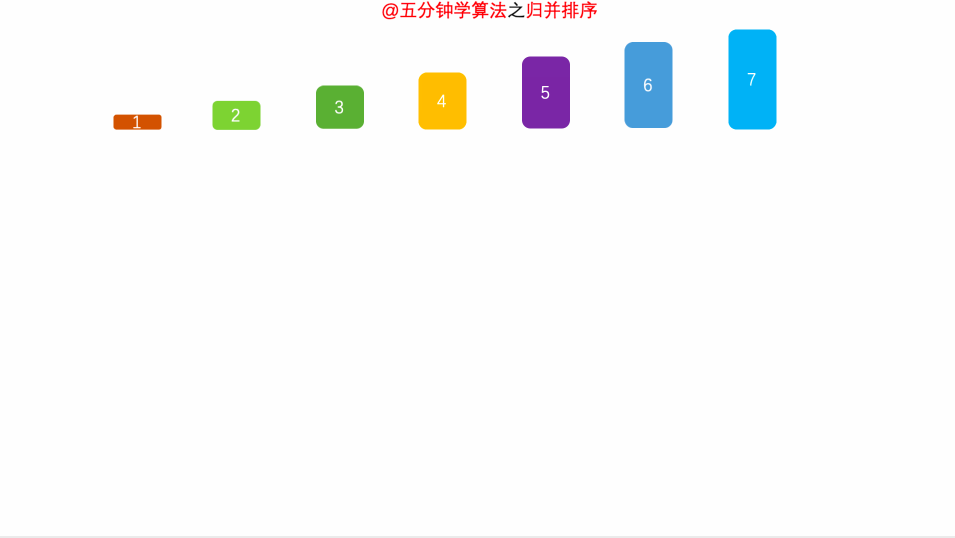
As can be seen from the above figure, merging sorting first divides a sequence into many subsequences, first makes these subsequences orderly, and then combines them into an orderly sequence. The idea of merging is to select elements according to the size in the two subsequences to make the two subsequences orderly, from bottom to top, until the whole sequence is orderly.

The code is as follows:

//Merge sort

void MergePartSort(int* a, int* arr, int left1, int right1, int left2, int right2)
{
	int ptr1 = left1, ptr2 = left2;
	int index = left1;//To be placed in the corresponding position
	//One of the two intervals stops at the end
	while (ptr1 <= right1 && ptr2 <= right2)
	{
		if (a[ptr1] < a[ptr2])
		{
			arr[index++] = a[ptr1];
			ptr1++;
		}
		else
		{
			arr[index++] = a[ptr2];
			ptr2++;
		}
	}
	//Just put all the remaining elements behind
	while (ptr1 <= right1)
	{
		arr[index++] = a[ptr1];
		ptr1++;
	}

	while (ptr2 <= right2)
	{
		arr[index++] = a[ptr2];
		ptr2++;
	}
}

void _MergeSort(int* a, int* arr, int left, int right, int n)
{
	if (left >= right)
	{
		return;
	}
	else
	{
		int mid = (left + right) >> 1;
		_MergeSort(a, arr, left, mid, n);
		_MergeSort(a, arr, mid + 1, right, n);
		//After the two sub intervals are found, they are merged and placed
		MergePartSort(a, arr, left, mid, mid + 1, right);
		//Merge and copy once
		//Don't use memcpy. When copying, just copy a certain interval. It is more flexible to use loop
		for (int i = left; i <= right; ++i)
			a[i] = arr[i];
	}
}


void MergeSort(int* a, int n)
{
	int* arr = (int*)malloc(sizeof(int)*n);
	if (arr == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	//Copy the elements of the original array to the new array
	_MergeSort(a, arr, 0, n - 1, n);
	free(arr);
}

The above explanation is the recursive version of merge sorting, so it can also be completed with non recursion.
The non recursive method is equivalent to merging each section of cells in the recursion, and then changing the length of cells by maintaining the variable gap until the sorting of left and right elements is completed.

There are three special situations to pay attention to when non recursive:
(1) The first is merging. When the second subinterval does not exist, the first subinterval is gap, so merging is not necessary, because this subinterval has been sorted in the previous gap.
(2) The second is that the second subinterval does not exist. If the first subinterval is not enough gap, there is no need to merge.

These two schemes can be summarized as that they do not need to merge and directly jump out of the loop.

(3) The third is that the second subinterval exists but there are not enough gap s, so you need to adjust the last begin2, otherwise it will cross the boundary. Adjust begin2 to reduce the length of the array by one.

void MergeSort_NonR(int* a, int n)
{
	int* arr = (int*)malloc(sizeof(int)*n);
	if (arr == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	int gap = 1;
	int i = 0;
	while (gap < n)
	{
		//gap refers to the interval between two sub intervals to be merged
		for (i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1, begin2 = i + gap, end2 = i + 2 * gap - 1;
			//For non recursive merging, there are three situations to pay attention to
			//The first is merging. When the second subinterval does not exist, the first subinterval is gap, so merging is not necessary, because this subinterval has been sorted in the previous gap
			//The second is that the second subinterval does not exist. If the first subinterval is not enough gap, there is no need to merge
			//To sum up, if the second subinterval does not exist, it does not need to be merged
			if (begin2 >= n)
				break;
			//The third is that the second subinterval exists but there are not enough gap s, so you need to adjust the last begin2, otherwise it will cross the boundary. Just adjust begin2 to the length of the array
			//This indicates that there is a second sub interval
			if (end2 >= n)
				end2 = n - 1;
			MergePartSort(a, arr, begin1, end1, begin2, end2);
		}

		gap *= 2;
	}
	//Release the open space
	free(arr);
}

Characteristics of merge sort:

1. The disadvantage of merging is that it requires O(N) space complexity. The thinking of merging sorting is more to solve the problem of external sorting in the disk.
2. Time complexity: O(N*logN)
3. Space complexity
4. Stability: stable

Non comparison sort

The most widely used non comparative sorting is counting sorting, which is used very much in OJ questions.
Steps of counting and sorting:
(1) Count the number of occurrences of the same element
(2) Put the data back into the original sequence according to the statistical results.

If the count array is a sorted positive integer array, the subscript does not need to be changed, but if there are negative numbers in the array, the value corresponding to the subscript needs to be changed, that is, the range represented by the subscript needs to be changed.
For example, to sort the numbers in the range of - 100 ~ 100, you need to open up an array with a length of 201, that is, add 100 to the subscript, so that the range represented by the subscript becomes 0 ~ 200, and then subtract 100 when restoring.

//Count sort

void CountSort(int* a, int n)
{
	int i = 0;
	//You can optimize the space complexity and open up a count array with a length of the largest element in the array
	int max = 0;
	for (i = 0; i < n; i++)
	{
		if (a[i] > max)
			max = a[i];
	}
	int* count = (int*)malloc(sizeof(int)*(max + 1));
	if (count == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	memset(count, 0, sizeof(int)*(max + 1));
	//Counts the number of occurrences of elements in the array
	for (i = 0; i < n; i++)
		count[a[i]]++;
	int index = 0;
	//Put the elements in the count array back into the original array
	for (i = 0; i < max + 1; i++)
	{
		while (count[i]--)
		{
			a[index++] = i;
		}
	}

	free(count);
}

Characteristics of count sorting:

1. When the counting sorting is in the data range set, the efficiency is very high, but the scope of application and scenarios are limited.
2. Time complexity: O(MAX(N, range))
3. Space complexity: O (range)
4. Stability: stable