[source code analysis] PyTorch distributed optimizer (1) -- Cornerstone
0x00 summary
Let's look at the distributed optimizer in a few articles. This series is divided into three articles: the cornerstone, the data parallel optimizer in DP/DDP/Horovod, and the PyTorch distributed optimizer, which are progressive in depth.
This article is the cornerstone. Through this article, you can understand the structure of the model, the basic principle of the optimizer, the interaction between the two, how to optimize and update the model, etc., which lays a foundation for the subsequent level-by-level analysis.
Other PyTorch distributed articles are as follows:
Automatic differentiation of deep learning tools (1)
Automatic differentiation of deep learning tools (2)
[Source code analysis] automatic differentiation of deep learning tools (3) - example interpretation
[Source code analysis] how PyTorch implements forward propagation (1) - basic class (1)
[Source code analysis] how PyTorch implements forward propagation (2) - basic classes (2)
[Source code analysis] how PyTorch implements forward propagation (3) - specific implementation
[Source code analysis] how pytoch implements backward propagation (1) -- call engine
[Source code analysis] how pytoch implements backward propagation (2) -- engine static structure
[Source code analysis] how pytoch implements backward propagation (3) -- engine dynamic logic
[Source code analysis] how PyTorch implements backward propagation (4) -- specific algorithm
[Source code analysis] PyTorch distributed (1) -- history and overview
[Source code analysis] PyTorch distributed (2) -- dataparallel (Part 1)
[Source code analysis] PyTorch distributed (3) -- dataparallel (Part 2)
[Source code analysis] PyTorch distributed (4) -- basic concept of distributed application
[Source code analysis] PyTorch distributed (5) -- overview of distributeddataparallel & how to use
[Source code analysis] PyTorch distributed (6) - DistributedDataParallel - initialize & store
[Source code analysis] PyTorch distributed (7) -- process group of distributeddataparallel
[Source code analysis] PyTorch distributed (8) -- distributed dataparallel
[Source code analysis] PyTorch distributed (9) -- initialization of distributeddataparallel
[Source code analysis] PyTorch distributed (12) -- distributeddataparallel forward propagation
[Source code analysis] PyTorch distributed (13) -- back propagation of distributed dataparallel
[Source code analysis] PyTorch distributed Autograd (1) -- Design
[Source code analysis] PyTorch distributed autograd (2) -- RPC Foundation
[Source code analysis] PyTorch distributed Autograd (3) -- context sensitive
[Source code analysis] PyTorch distributed Autograd (4) -- how to cut into the engine
[Source code analysis] PyTorch distributed Autograd (5) -- engine (I)
[Source code analysis] PyTorch distributed Autograd (6) -- engine (Part 2)
For better explanation, the code in this article will be simplified according to the specific situation.
0x01 starting from the problem
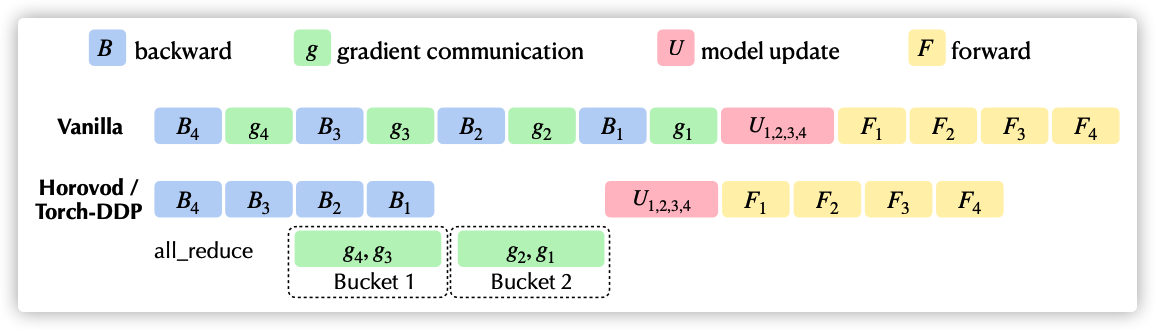
The following is a Kwai Lok paper. The chart shows the comparison between the native training process and DDP/Horovod. The vanilla above is the native training process, where the U part corresponds to the optimizer process. The main function of the general optimizer is to optimize & update the current parameters of the model according to the gradient: w.data -= w.grad * lr.
1.1 example
Let's use an example to see how to train.
class ToyModel(nn.Module):
def __init__(self):
super(ToyModel, self).__init__()
self.net1 = nn.Linear(10, 10)
self.relu = nn.ReLU()
self.net2 = nn.Linear(10, 5)
def forward(self, x):
return self.net2(self.relu(self.net1(x)))
net = ToyModel()
optimizer = optim.SGD(params=net.parameters(), lr = 1)
optimizer.zero_grad()
input = torch.randn(10,10)
outputs = net(input)
outputs.backward(outputs)
optimizer.step()
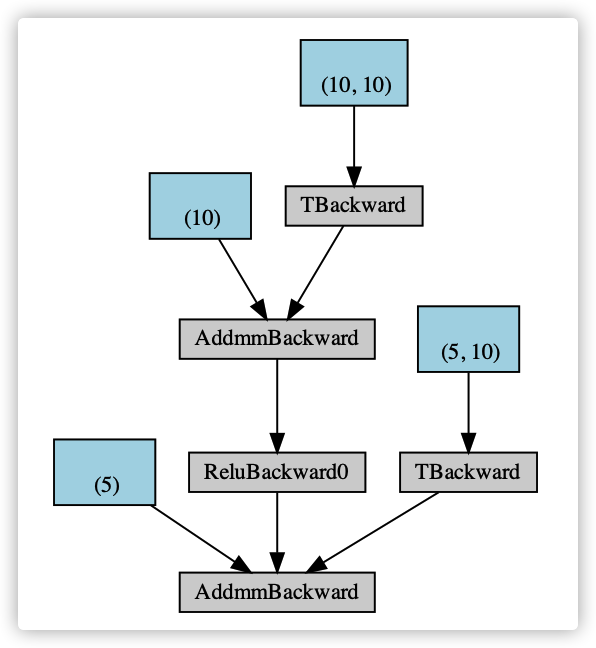
A rough reverse calculation diagram is given as follows.
1.2 problem points
Because we have other experiences such as the previous analysis engine, we have sorted out several problem points in combination with the previous knowledge to guide our analysis. We analyze in the order of building the optimizer according to the model parameters - > engine calculation gradient - > optimizer optimization parameters - > optimizer updating the model. We know that the autograd engine calculates the gradient, so the problem comes:
-
Build optimizer based on model parameters
- It is constructed with optimizer = optim. SGD (parameters = net. Parameters(), LR = 1), so it looks like parameters are assigned to the internal member variables of the optimizer (we assume they are called parameters).
-
- The model includes two Linear layers. How do these layers update parameters?
-
Engine calculation gradient
- How to ensure that Linear can calculate gradients?
-
- For the model, how does the calculated gradient correspond to the Linear parameter? Where do these gradients calculated by the engine accumulate?
-
Optimizer optimization parameters:
-
- Call step for optimization. The optimization goal is the internal member variable self.parameters of the optimizer.
-
-
Optimizer update model:
-
- How to reflect the update of optimization objectives (self.parameters) to the update of model parameters (such as Linear)?
-
The numbers and question marks in the figure below correspond to the above four questions.
+-------------------------------------------+ +------------------+
|ToyModel | | Engine |
| | forward / backward | |
| Linear(10, 10)+--> ReLU +--> Linear(10, 5)| +----------------> | Compute gradient |
| | | + |
+-------------------+-----------------------+ | | |
| | | |
1 ??? | parameters() +------------------+
| |
| | gradient
| ^ |
| | v
| | 4 ??? 2 ???
| |
+------------------------------------------+
|SGD | | |
| | | |
| v + |
| |
^ +---------------> self.parameters +---------------->
| | | |
| | | |
| +------------------------------------------+ |
| |
<---------------------------------------------------+ v
3 step()
We need to analyze it step by step.
0x01 model construction
Since the optimizer is the parameter to optimize and update the model, let's first introduce the model related information.
1.1 Module
If you define a model in PyTorch, you generally need to inherit nn.Module.
import torch
import torch.nn as nn
import torch.nn.functional as F
class ToyModel(nn.Module):
def __init__(self):
super(ToyModel, self).__init__()
self.net1 = nn.Linear(10, 10)
self.relu = nn.ReLU()
self.net2 = nn.Linear(10, 5)
def forward(self, x):
return self.net2(self.relu(self.net1(x)))
Module is defined as follows:
class Module:
r"""Base class for all neural network modules.
Your models should also subclass this class.
Modules can also contain other Modules, allowing to nest them in
a tree structure. You can assign the submodules as regular attributes::
import torch.nn as nn
import torch.nn.functional as F
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.conv1 = nn.Conv2d(1, 20, 5)
self.conv2 = nn.Conv2d(20, 20, 5)
def forward(self, x):
x = F.relu(self.conv1(x))
return F.relu(self.conv2(x))
Submodules assigned in this way will be registered, and will have their
parameters converted too when you call :meth:`to`, etc.
:ivar training: Boolean represents whether this module is in training or
evaluation mode.
:vartype training: bool
"""
dump_patches: bool = False
_version: int = 1
training: bool
_is_full_backward_hook: Optional[bool]
def __init__(self):
"""
Initializes internal Module state, shared by both nn.Module and ScriptModule.
"""
torch._C._log_api_usage_once("python.nn_module")
self.training = True
self._parameters = OrderedDict()
self._buffers = OrderedDict()
self._non_persistent_buffers_set = set()
self._backward_hooks = OrderedDict()
self._is_full_backward_hook = None
self._forward_hooks = OrderedDict()
self._forward_pre_hooks = OrderedDict()
self._state_dict_hooks = OrderedDict()
self._load_state_dict_pre_hooks = OrderedDict()
self._modules = OrderedDict()
1.2 member variables
There are the following important variables inside the Module, which can be roughly divided into the following three categories.
Foundation type:
- _ Parameters: weight parameters of tensor type, which are used for forward and backward propagation. Saving the model is to save these parameters. You can get all the parameters of the model recursively by using the parameters() function, but note that the parameters() function returns the iterator.
- _ buffers: stores variables of non network parameters that need to be persisted, such as BN's running_mean.
- _ modules: stores variables of type Module. When you go to the parameters of a model, PyTorch recursively traverses all variables_ modules.
Calculation related types:
During model calculation, it is completed in the following order:
_backward_hooks ----> forward ----> _forward_hooks ----> _backward_hooks
The details are as follows:
-
_ forward_pre_hooks: runs before forward and does not change the forward input parameter.
-
_ forward_hooks: runs after forward and does not change the input and output of forward.
-
_ backward_hooks: runs after backward and does not change the input and output of backward.
Save / load related:
The following is related to saving. PyTorch saves torch.save(cn.state_dict()...) and load_state_dict(state_dict).
- _ load_state_dict_pre_hooks: when calling_ load_ from_ state_ What you want to do when dict loads the model.
- _ state_dict_hooks: when calling state_ What you want to do when using the dict method.
The specific operation time is as follows:
net = {ToyModel}
T_destination = {TypeVar} ~T_destination
dump_patches = {bool} False
net1 = {Linear} Linear(in_features=10, out_features=10, bias=True)
net2 = {Linear} Linear(in_features=10, out_features=5, bias=True)
relu = {ReLU} ReLU()
training = {bool} True
_backward_hooks = {OrderedDict: 0} OrderedDict()
_buffers = {OrderedDict: 0} OrderedDict()
_forward_hooks = {OrderedDict: 0} OrderedDict()
_forward_pre_hooks = {OrderedDict: 0} OrderedDict()
_is_full_backward_hook = {NoneType} None
_load_state_dict_pre_hooks = {OrderedDict: 0} OrderedDict()
_modules = {OrderedDict: 3} OrderedDict([('net1', Linear(in_features=10, out_features=10, bias=True)), ('relu', ReLU()), ('net2', Linear(in_features=10, out_features=5, bias=True))])
_non_persistent_buffers_set = {set: 0} set()
_parameters = {OrderedDict: 0} OrderedDict()
_state_dict_hooks = {OrderedDict: 0} OrderedDict()
_version = {int} 1
1.3 _parameters
The optimizer is optimized_ parameters, so we need a special understanding.
1.3.1 construction
Let's first look at the characteristics of generation: requirements_ grad=True. If the Parameter is set in this way, it means that the gradient needs to be calculated for the Parameter.
Because the tensor does not need derivation by default_ The grad attribute defaults to False if a node requires_ If the grad property is set to True, it means that it needs derivation, and all nodes that depend on it require derivation_ Grad is True.
class Parameter(torch.Tensor):
r"""A kind of Tensor that is to be considered a module parameter.
Parameters are :class:`~torch.Tensor` subclasses, that have a
very special property when used with :class:`Module` s - when they're
assigned as Module attributes they are automatically added to the list of
its parameters, and will appear e.g. in :meth:`~Module.parameters` iterator.
Assigning a Tensor doesn't have such effect. This is because one might
want to cache some temporary state, like last hidden state of the RNN, in
the model. If there was no such class as :class:`Parameter`, these
temporaries would get registered too.
Args:
data (Tensor): parameter tensor.
requires_grad (bool, optional): if the parameter requires gradient. See
:ref:`locally-disable-grad-doc` for more details. Default: `True`
"""
def __new__(cls, data=None, requires_grad=True): # The gradient needs to be calculated
if data is None:
data = torch.tensor([])
return torch.Tensor._make_subclass(cls, data, requires_grad)
1.3.2 classification
If the member of the class is derived from the Parameter class, nn.Module uses__ setattr__ The mechanism attributed them to_ parameters. Such as Linear's weight and bias.
def __setattr__(self, name: str, value: Union[Tensor, 'Module']) -> None:
# Omit
params = self.__dict__.get('_parameters')
if isinstance(value, Parameter):
remove_from(self.__dict__, self._buffers, self._modules, self._non_persistent_buffers_set)
self.register_parameter(name, value) #
def register_parameter(self, name: str, param: Optional[Parameter]) -> None:
r"""Adds a parameter to the module.
The parameter can be accessed as an attribute using given name.
Args:
name (string): name of the parameter. The parameter can be accessed
from this module using the given name
param (Parameter): parameter to be added to the module.
"""
# Omit various checks
if param is None:
self._parameters[name] = None
elif not isinstance(param, Parameter):
raise TypeError("cannot assign '{}' object to parameter '{}' "
"(torch.nn.Parameter or None required)"
.format(torch.typename(param), name))
elif param.grad_fn:
raise ValueError(
"Cannot assign non-leaf Tensor to parameter '{0}'. Model "
"parameters must be created explicitly. To express '{0}' "
"as a function of another Tensor, compute the value in "
"the forward() method.".format(name))
else:
self._parameters[name] = param # Added here
1.3.3 acquisition
We can't get it directly_ The parameters variable can only be obtained through the parameters method, and it returns an Iterator.
For example:
for param in net.parameters():
print(type(param), param.size())
Output:
<class 'torch.nn.parameter.Parameter'> torch.Size([10, 10]) <class 'torch.nn.parameter.Parameter'> torch.Size([10]) <class 'torch.nn.parameter.Parameter'> torch.Size([5, 10]) <class 'torch.nn.parameter.Parameter'> torch.Size([5])
The parameters code is as follows.
def parameters(self, recurse: bool = True) -> Iterator[Parameter]:
r"""Returns an iterator over module parameters.
This is typically passed to an optimizer.
Args:
recurse (bool): if True, then yields parameters of this module
and all submodules. Otherwise, yields only parameters that
are direct members of this module.
Yields:
Parameter: module parameter
Example::
>>> for param in model.parameters():
>>> print(type(param), param.size())
<class 'torch.Tensor'> (20L,)
<class 'torch.Tensor'> (20L, 1L, 5L, 5L)
"""
for name, param in self.named_parameters(recurse=recurse):
yield param
Let's look at named_parameters, whose core is module_ Parameters. Items(), return a traversable tuple array as a list.
def named_parameters(self, prefix: str = '', recurse: bool = True) -> Iterator[Tuple[str, Parameter]]:
r"""Returns an iterator over module parameters, yielding both the
name of the parameter as well as the parameter itself.
Args:
prefix (str): prefix to prepend to all parameter names.
recurse (bool): if True, then yields parameters of this module
and all submodules. Otherwise, yields only parameters that
are direct members of this module.
Yields:
(string, Parameter): Tuple containing the name and parameter
Example::
>>> for name, param in self.named_parameters():
>>> if name in ['bias']:
>>> print(param.size())
"""
gen = self._named_members(
lambda module: module._parameters.items(),
prefix=prefix, recurse=recurse)
for elem in gen:
yield elem
It should be noted that we already have two key knowledge:
- Parameter requires in parameter constructor_ grad=True. This setting indicates that the parameter needs to calculate the gradient by default.
- It is obtained through the parameters method, which returns an Iterator.
Therefore, the previous figure can be expanded. Now the parameters of SGD point to ToyModel_ The iterator of parameters, which shows that the optimizer actually optimizes the ToyModel directly_ parameters. So we can remove the question mark corresponding to 4) in the original figure.
+-------------------------------------------+ +------------------+
|ToyModel | | Engine |
| | forward / backward | |
| Linear(10, 10)+--> ReLU +--> Linear(10, 5)| +----------------> | Compute gradient |
| | | + |
| para_iterator = parameters() | | | |
| + ^ | | | |
| | | | +------------------+
+-------------------------------------------+ |
| | | gradient
| | |
1 ??? | | 4 update v
| | 2 ???
| |
+----------------------------------------------------------------+
|SGD | | |
| | | |
| v | |
| + |
^ +--------> self.parameters = para_iterator(ToyModel._parameters) --------->
| | | |
| | | |
| +----------------------------------------------------------------+ |
| |
<-------------------------------------------------------------------------+ v
3 step()
1.4 Linear
Torch.nn.Linear can realize linear transformation of input data, which is generally used to set the full connection layer.
1.4.1 use
The example of using torch.nn.Linear in PyTorch is as follows.
input = torch.randn(2,3)
linear = nn.Linear(3,4)
out = linear(input)
print(out)
# The output results are as follows
tensor([[-0.6938, 0.0543, -1.4393, -0.3554],
[-0.4653, -0.2421, -0.8236, -0.1872]], grad_fn=<AddmmBackward>)
1.4.2 definitions
The specific definitions of Linear are as follows. You can see that its parameters are mainly
- self.weight = Parameter().
- self.bias = Parameter().
As we can see from the above, the Parameter is required when generating the Parameter_ Grad = true, indicating that the gradient of weight and bias needs to be calculated.
class Linear(Module):
r"""Applies a linear transformation to the incoming data: :math:`y = xA^T + b`
This module supports :ref:`TensorFloat32<tf32_on_ampere>`.
Args:
in_features: size of each input sample
out_features: size of each output sample
bias: If set to ``False``, the layer will not learn an additive bias.
Default: ``True``
Shape:
- Input: :math:`(N, *, H_{in})` where :math:`*` means any number of
additional dimensions and :math:`H_{in} = \text{in\_features}`
- Output: :math:`(N, *, H_{out})` where all but the last dimension
are the same shape as the input and :math:`H_{out} = \text{out\_features}`.
Attributes:
weight: the learnable weights of the module of shape
:math:`(\text{out\_features}, \text{in\_features})`. The values are
initialized from :math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})`, where
:math:`k = \frac{1}{\text{in\_features}}`
bias: the learnable bias of the module of shape :math:`(\text{out\_features})`.
If :attr:`bias` is ``True``, the values are initialized from
:math:`\mathcal{U}(-\sqrt{k}, \sqrt{k})` where
:math:`k = \frac{1}{\text{in\_features}}`
Examples::
>>> m = nn.Linear(20, 30)
>>> input = torch.randn(128, 20)
>>> output = m(input)
>>> print(output.size())
torch.Size([128, 30])
"""
__constants__ = ['in_features', 'out_features']
in_features: int
out_features: int
weight: Tensor
def __init__(self, in_features: int, out_features: int, bias: bool = True,
device=None, dtype=None) -> None:
factory_kwargs = {'device': device, 'dtype': dtype}
super(Linear, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.empty((out_features, in_features), **factory_kwargs))
if bias:
self.bias = Parameter(torch.empty(out_features, **factory_kwargs))
else:
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self) -> None:
init.kaiming_uniform_(self.weight, a=math.sqrt(5))
if self.bias is not None:
fan_in, _ = init._calculate_fan_in_and_fan_out(self.weight)
bound = 1 / math.sqrt(fan_in) if fan_in > 0 else 0
init.uniform_(self.bias, -bound, bound)
def forward(self, input: Tensor) -> Tensor:
return F.linear(input, self.weight, self.bias)
def extra_repr(self) -> str:
return 'in_features={}, out_features={}, bias={}'.format(
self.in_features, self.out_features, self.bias is not None
)
1.4.3 interpretation
From the previous brief calculation diagram, we can know that the reverse calculation of torch.nn.Linear is AddmmBackward.
struct TORCH_API AddmmBackward : public TraceableFunction {
using TraceableFunction::TraceableFunction;
variable_list apply(variable_list&& grads) override;
std::string name() const override { return "AddmmBackward"; }
void release_variables() override {
std::lock_guard<std::mutex> lock(mutex_);
mat2_.reset_data();
mat1_.reset_data();
}
std::vector<int64_t> mat1_sizes;
std::vector<int64_t> mat1_strides;
SavedVariable mat2_;
at::Scalar alpha;
SavedVariable mat1_;
std::vector<int64_t> mat2_sizes;
std::vector<int64_t> mat2_strides;
at::Scalar beta;
};
We found the definition of addmm from the code, and its annotation indicates that this is a matrix multiplication operation.
def addmm(mat: Tensor, mat1: Tensor, mat2: Tensor,
beta: float = 1., alpha: float = 1.) -> Tensor:
r"""
This function does exact same thing as :func:`torch.addmm` in the forward,
except that it supports backward for sparse matrix :attr:`mat1`. :attr:`mat1`
need to have `sparse_dim = 2`. Note that the gradients of :attr:`mat1` is a
coalesced sparse tensor.
Args:
mat (Tensor): a dense matrix to be added
mat1 (Tensor): a sparse matrix to be multiplied
mat2 (Tensor): a dense matrix to be multiplied
beta (Number, optional): multiplier for :attr:`mat` (:math:`\beta`)
alpha (Number, optional): multiplier for :math:`mat1 @ mat2` (:math:`\alpha`)
"""
return torch._sparse_addmm(mat, mat1, mat2, beta=beta, alpha=alpha)
At present, we can continue to expand.
- weight and bias in Linear are Parameter types.
- Parameter requires in parameter constructor_ grad=True. This setting indicates that the parameter needs to calculate the gradient by default.
- Therefore, Linear weight and bias require the engine to calculate its gradient.
- Of ToyModel_ The parameters member variable is obtained through the parameters method, which returns an Iterator.
- This iterator is used as a parameter to build the SGD optimizer.
- Now the parameters of the SGD optimizer is a pointer to ToyModel_ iterator for parameters. This shows that the optimizer actually optimizes the ToyModel directly_ Parameters, for example, the parameters of the full connection layer, correspond to the arrows pointing to parameters() issued by two Linear on the figure.
+--------------------------------------------------+ +------------------+
| ToyModel | | Engine |
| +-------------------+ +------------+ |forward / backward | |
| | Linear(10, 10) +--> ReLU +-->+Linear(10,5)| +-----------------> | Compute gradient |
| | | | | | | + |
| | weight=Parameter | | weight | | | | |
| | +----------+ | | | | | |
| | bias=Parameter | | | bias | | +------------------+
| | | | | | | |
| +-------------------+ | +--+---------+ | 2 | gradient
| | | | |
| | | | v
| v v | ???
| para_iterator = parameters() |
| + ^ |
| | | |
| | | |
+--------------------------------------------------+
| |
1 ??? | | 4 update
| |
| |
+----------------------------------------------------------------+
|SGD | | |
| | | |
| v | |
| + |
^ +--------> self.parameters = para_iterator(ToyModel._parameters) +-------->
| | | |
| | | |
| +----------------------------------------------------------------+ |
| |
<-------------------------------------------------------------------------+ v
3 step()
0x02 Optimizer base class
Optimizer is the base class of all optimizers. It has the following main public methods:
- add_param_group: add a learnable parameter group.
- step: update parameters once.
- zero_grad: clear the gradient at the last iteration before calculating the gradient by back propagation.
- state_dict: returns the parameters and status represented by the dict structure.
- load_state_dict: load the parameters and states represented by the dict structure.
2.1 initialization
In the Optimizer initialization function, the following operations will be performed:
- Initialization parameters include: learnable parameters (params) and super parameters (defaults).
- Save global parameters (super parameters) such as LR and momentun in self.defaults.
- Save the current state of the optimizer in self.state.
- In self.param_ Save all variables to be optimized in groups.
class Optimizer(object):
def __init__(self, params, defaults):
torch._C._log_api_usage_once("python.optimizer")
self.defaults = defaults # Save global parameters such as LR and momentun
self._hook_for_profile()
if isinstance(params, torch.Tensor): # params must be a dictionary or tensors
raise TypeError("params argument given to the optimizer should be "
"an iterable of Tensors or dicts, but got " +
torch.typename(params))
self.state = defaultdict(dict) # Saves the current state of the optimizer
self.param_groups = [] # For all parameters to be optimized, each item is a dictionary, corresponding to a group of parameters to be optimized and other related parameters
param_groups = list(params) # The variables to be optimized are__ init__ Parameters passed in
if len(param_groups) == 0:
raise ValueError("optimizer got an empty parameter list")
if not isinstance(param_groups[0], dict):
# Convert parameters to dictionaries
param_groups = [{'params': param_groups}] # param_groups is a list, one of which is in the form of a dictionary, in which the optimization variables are saved.
for param_group in param_groups:
self.add_param_group(param_group) # Param_ All groups items are added to self.param_ In groups
2.2 adding variables to be optimized
Add is used in the above code_ param_ Group, let's take a look at this function.
add_param_group add learnable parameters for different groups. The code is as follows (most inspection codes are omitted). Where param_ The purpose of groups is to access the variables to be optimized in key value mode, which is particularly useful in fine tuning.
def add_param_group(self, param_group):
r"""Add a param group to the :class:`Optimizer` s `param_groups`.
This can be useful when fine tuning a pre-trained network as frozen layers can be made
trainable and added to the :class:`Optimizer` as training progresses.
Args:
param_group (dict): Specifies what Tensors should be optimized along with group
specific optimization options.
"""
assert isinstance(param_group, dict), "param group must be a dict"
params = param_group['params'] # Get the variables to be optimized
if isinstance(params, torch.Tensor):
param_group['params'] = [params] # Build a list of variables to be optimized
elif isinstance(params, set):
raise TypeError('optimizer parameters need to be organized in ordered collections, but '
'the ordering of tensors in sets will change between runs. Please use a list instead.')
else:
param_group['params'] = list(params)
# Omit verification. For example, it must be a tensor type and a leaf node
for name, default in self.defaults.items(): # Default parameters are also added to param_group
if default is required and name not in param_group:
raise ValueError("parameter group didn't specify a value of required optimization parameter " +
name)
else:
param_group.setdefault(name, default) # All groups set the same default parameters (super parameters)
# Use set to remove duplicate
params = param_group['params']
param_set = set()
for group in self.param_groups:
param_set.update(set(group['params']))
# Update in its own parameter group
self.param_groups.append(param_group) # Add to param_groups
2.3 examples of variables to be optimized
We print param with the following code_ Groups come out and have a look.
net = nn.Linear(3, 3) nn.init.constant_(net.weight, val=10) nn.init.constant_(net.bias, val=5) optimizer = optim.SGD(net.parameters(), lr=0.025) print(optimizer.param_groups)
The results are as follows. The first 3 x 3 is the weight matrix of net and 1 x 3 is the offset matrix.
[
{'params':
[
Parameter containing: # Weight matrix
tensor([[10., 10., 10.],
[10., 10., 10.],
[10., 10., 10.]], requires_grad=True),
Parameter containing: # Offset matrix
tensor([5., 5., 5.], requires_grad=True)
],
'lr': 0.025,
'momentum': 0,
'dampening': 0,
'weight_decay': 0,
'nesterov': False
}
]
2.4 optimizer status
2.4.1 definitions
State of PyTorch_ Dict is a Python dictionary object.
-
For models, state_dict will establish a mapping relationship between each layer and the parameters to be learned in the training process (such as weight and bias). Only the layers whose parameters can be trained will be saved in the state of the model_ In dict, such as convolution layer, linear layer, etc.
-
For the optimizer, state_dict is its status information, which includes two groups of information:
- State: a dictionary that includes the current state of the optimizer (that is, the latest cached variable calculated during variable update).
- The key of the dictionary is the cached index.
- The value of the dictionary is also a dictionary, key is the name of the cache variable, and value is the corresponding tensor.
- param_groups: a dictionary that includes all param groups.
- State: a dictionary that includes the current state of the optimizer (that is, the latest cached variable calculated during variable update).
def state_dict(self):
r"""Returns the state of the optimizer as a :class:`dict`.
It contains two entries:
* state - a dict holding current optimization state. Its content
differs between optimizer classes.
* param_groups - a dict containing all parameter groups
"""
# Save order indices instead of Tensors
param_mappings = {}
start_index = 0
def pack_group(group):
nonlocal start_index
# 'params' uses different rules
packed = {k: v for k, v in group.items() if k != 'params'}
param_mappings.update({id(p): i for i, p in enumerate(group['params'], start_index)
if id(p) not in param_mappings})
# The id of the parameter is saved instead of the value of the parameter
packed['params'] = [param_mappings[id(p)] for p in group['params']]
start_index += len(packed['params'])
return packed
# For self.param_groups to traverse and pack
param_groups = [pack_group(g) for g in self.param_groups]
# Replace all tensors in the state with the corresponding use order indexes
# Remap state to use order indices as keys
packed_state = {(param_mappings[id(k)] if isinstance(k, torch.Tensor) else k): v
for k, v in self.state.items()}
return { # Return dictionary form
'state': packed_state, # state
'param_groups': param_groups, # Parameters to be optimized
}
2.4.2 example 1
We added the following print statement in example 1 to see the internal variables of the optimizer:
# print model's state_dict
print('Model.state_dict:')
for param_tensor in model.state_dict():
print(param_tensor, '\t', model.state_dict()[param_tensor].size())
# print optimizer's state_dict
print('Optimizer,s state_dict:')
for var_name in optimizer.state_dict():
print(var_name, '\t', optimizer.state_dict()[var_name])
The results are as follows:
Model.state_dict:
net1.weight torch.Size([10, 10])
net1.bias torch.Size([10])
net1.weight torch.Size([10, 10])
net2.bias torch.Size([5])
Optimizer,s state_dict:
state {}
param_groups [{'lr': 0.001, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0, 1, 2, 3]}]
2.4.3 example 2
Example 2 is to optimize a function using SGD.
from math import pi
import torch.optim
x = torch.tensor([pi/2,pi/3],requires_grad=True)
optimizer = torch.optim.SGD([x,],lr=0.2,momentum=0.5)
for step in range(11):
if step:
optimizer.zero_grad()
f.backward()
optimizer.step()
for var_name in optimizer.state_dict():
print(var_name, '\t', optimizer.state_dict()[var_name])
f=-((x.sin()**3).sum())**3
The output results are as follows, which shows the optimization process.
state {0: {'momentum_buffer': tensor([ 1.0704e-06, -9.1831e+00])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
state {0: {'momentum_buffer': tensor([-1.2757e-06, -4.0070e+00])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
state {0: {'momentum_buffer': tensor([-3.4580e-07, -4.7366e-01])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
state {0: {'momentum_buffer': tensor([7.3855e-07, 1.3584e+00])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
state {0: {'momentum_buffer': tensor([7.2726e-07, 1.6619e+00])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
state {0: {'momentum_buffer': tensor([-3.1580e-07, 8.4152e-01])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
state {0: {'momentum_buffer': tensor([2.3738e-07, 5.8072e-01])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
state {0: {'momentum_buffer': tensor([5.2412e-07, 8.4104e-01])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
state {0: {'momentum_buffer': tensor([-5.1160e-07, 1.9660e+00])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
state {0: {'momentum_buffer': tensor([4.9517e-07, 7.2053e+00])}}
param_groups [{'lr': 0.2, 'momentum': 0.5, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}]
Let's update and make sure that the name of the member variable inside SGD is param_groups, which is the optimization goal of the optimizer, points to toymodel_ iterator for parameters.
+-------------------------------------------------+ +------------------+
|ToyModel | | Engine |
| +------------------+ +------------+ |forward / backward | |
| |Linear(10, 10) +--> ReLU +-->+Linear(10,5)| +-----------------> | Compute gradient |
| | | | | | | + |
| | weight=Parameter| | weight | | | | |
| | +-----------+ | bias | | | | |
| | bias=Parameter | | +--+---------+ | +------------------+
| | | | | | |
| +------------------+ | | | 2 | gradient
| v v | |
| self._parameters | v
| + | ???
| | |
| | |
| v |
| para_iterator = parameters() |
| + ^ |
| | | |
| | | |
+-------------------------------------------------+
| |
1 ??? | | 4 update
| |
+----------------------------------------------------------------+
|SGD | | |
| | | |
| v | |
| + |
^ +-------> self.param_groups = para_iterator(ToyModel._parameters) -------->
| | | |
| | | |
| +----------------------------------------------------------------+ |
| |
<-------------------------------------------------------------------------+ v
3 step()
0x03 SGD
Let's take a closer look at the optimizer with SGD. SGD (stochastic gradient descent) is a batch version of random gradient descent, that is, gradient descent. For the training data set, it is divided into n batches, and each batch contains m samples. Each update uses the data of one batch instead of the whole training set.
3.1 definitions
SGD is defined as follows. It is mainly used to perform checksum and set the default value.
class SGD(Optimizer):
def __init__(self, params, lr=required, momentum=0, dampening=0,
weight_decay=0, nesterov=False):
if lr is not required and lr < 0.0:
raise ValueError("Invalid learning rate: {}".format(lr))
if momentum < 0.0:
raise ValueError("Invalid momentum value: {}".format(momentum))
if weight_decay < 0.0:
raise ValueError("Invalid weight_decay value: {}".format(weight_decay))
defaults = dict(lr=lr, momentum=momentum, dampening=dampening,
weight_decay=weight_decay, nesterov=nesterov)
if nesterov and (momentum <= 0 or dampening != 0):
raise ValueError("Nesterov momentum requires a momentum and zero dampening")
super(SGD, self).__init__(params, defaults)
def __setstate__(self, state):
super(SGD, self).__setstate__(state)
for group in self.param_groups:
group.setdefault('nesterov', False)
3.2 analysis
As can be seen from the comments, SGD implements the stochastic gradient descent (optically with momentum) algorithm. Nesterov momentum is based on [on the importance of initialization and momentum in deep learning]( http://www.cs.toronto.edu/%7Ehinton/absps/momentum.pdf ). algorithm.
Use examples are as follows:
Example:
>>> optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
>>> optimizer.zero_grad()
>>> loss_fn(model(input), target).backward()
>>> optimizer.step()
The implementation of PyTorch SGD with Momentum/Nesterov is different from that of sutskever et al. And other frameworks.
For example, PyTorch uses the following methods to implement a special example of Momentum:
v
t
+
1
=
μ
∗
v
t
+
g
t
+
1
,
p
t
+
1
=
p
t
−
lr
∗
v
t
+
1
,
\begin{aligned} v_{t+1} & = \mu * v_{t} + g_{t+1}, \\ p_{t+1} & = p_{t} - \text{lr} * v_{t+1}, \end{aligned}
vt+1pt+1=μ∗vt+gt+1,=pt−lr∗vt+1,
Other frameworks use:
v
t
+
1
=
μ
∗
v
t
+
lr
∗
g
t
+
1
,
p
t
+
1
=
p
t
−
v
t
+
1
.
\begin{aligned} v_{t+1} & = \mu * v_{t} + \text{lr} * g_{t+1}, \\ p_{t+1} & = p_{t} - v_{t+1}. \end{aligned}
vt+1pt+1=μ∗vt+lr∗gt+1,=pt−vt+1.
3.3 step
The function of step method is to optimize the variables with the help of a certain algorithm. This method mainly completes the update of model parameters once
@torch.no_grad()
def step(self, closure=None):
"""Performs a single optimization step.
Args:
closure (callable, optional): A closure that reevaluates the model
and returns the loss.
"""
# Recalculate loss using closure
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
# Update the variable using the calculated gradient
# self.param_groups is the parameter list we passed in
for group in self.param_groups: # Each group is a dict that contains the necessary parameters required for each group of parameters
params_with_grad = []
d_p_list = []
momentum_buffer_list = []
# Settings required for updating this group of parameters
weight_decay = group['weight_decay']
momentum = group['momentum']
dampening = group['dampening']
nesterov = group['nesterov']
lr = group['lr']
for p in group['params']: # Traverse all parameters to be updated in this group
if p.grad is not None:
params_with_grad.append(p)
d_p_list.append(p.grad)
state = self.state[p]
if 'momentum_buffer' not in state:
momentum_buffer_list.append(None)
else:
momentum_buffer_list.append(state['momentum_buffer'])
F.sgd(params_with_grad,
d_p_list,
momentum_buffer_list,
weight_decay=weight_decay,
momentum=momentum,
lr=lr,
dampening=dampening,
nesterov=nesterov)
# update momentum_buffers in state
for p, momentum_buffer in zip(params_with_grad, momentum_buffer_list):
state = self.state[p]
state['momentum_buffer'] = momentum_buffer
return loss
The sgd function is as follows:
def sgd(params: List[Tensor],
d_p_list: List[Tensor],
momentum_buffer_list: List[Optional[Tensor]],
*,
weight_decay: float,
momentum: float,
lr: float,
dampening: float,
nesterov: bool):
r"""Functional API that performs SGD algorithm computation.
See :class:`~torch.optim.SGD` for details.
"""
for i, param in enumerate(params):
d_p = d_p_list[i]
# Regularization and momentum accumulation
if weight_decay != 0:
d_p = d_p.add(param, alpha=weight_decay)
if momentum != 0:
buf = momentum_buffer_list[i]
if buf is None:
# Historical update
buf = torch.clone(d_p).detach()
momentum_buffer_list[i] = buf
else:
# Updated self.state via buf
buf.mul_(momentum).add_(d_p, alpha=1 - dampening)
if nesterov:
d_p = d_p.add(buf, alpha=momentum)
else:
d_p = buf
# Update the current group learning parameter w.data -= w.grad*lr
param.add_(d_p, alpha=-lr) # add_ Changes the object value
3.4 variable analysis
Next, we will analyze the global parameters as follows.
3.4.1 lr
This is the learning rate, a well-known concept.
3.4.2 dampening
dampening acts on partial derivatives and adjusts the current gradient weight in momentum SGD.
The corresponding formula is as follows:
v
t
=
v
t
−
1
∗
m
o
m
e
n
t
u
m
+
g
t
∗
(
1
−
d
a
m
p
e
n
i
n
g
)
v_t = v_{t-1} * momentum + g_t * (1 - dampening)
vt=vt−1∗momentum+gt∗(1−dampening)
The corresponding code is:
buf.mul_(momentum).add_(d_p, alpha=1 - dampening)
3.4.3 weight_decay
weight_decay is the L2 penalty coefficient, which modifies the partial derivative with the value of the current learnable parameter p.
The partial derivative of the learnable parameter p to be updated is
g
t
=
g
t
+
(
p
∗
w
e
i
g
h
t
_
d
e
c
a
y
)
g_t = g_t + ( p * weight\_decay)
gt=gt+(p∗weight_decay)
The corresponding code is:
if weight_decay != 0: d_p = d_p.add(param, alpha=weight_decay)
3.4.4 nesterov
Whether to enable nesterov momentum. From the source code of pytorch, when nesterov is True, V is obtained above_ Momentum and V are used again on the basis of T_ t.
▽ w J ( w ) + m ∗ v t + 1 \bigtriangledown_{w}J(w) + m * v_{t+1} ▽wJ(w)+m∗vt+1
if (nesterov) {
d_p = d_p.add(buf, momentum);
} else {
d_p = buf;
}
3.4.5 Momentum
Momentum: from physics, translated as momentum or impulse. The function is to combine the last update with the current gradient to optimize and update the current weight.
The reason is that the initialization weight of the training network may be inappropriate, resulting in a local minimum in the training process, and the global optimum is not found.
The introduction of momentum can solve this problem to a certain extent. Momentum simulates the inertia of an object in motion and represents the cumulative effect of force on time. When updating, keep the previous update direction to a certain extent, and adjust the update direction in combination with the current gradient. The greater the momentum, the greater the energy converted into potential energy, which can increase stability and learn faster, so it is more likely to get rid of the local concave region and enter the global concave region.
The original weight update formula is as follows:
w
=
w
−
L
r
∗
d
w
w = w - Lr * dw
w=w−Lr∗dw
Here w is the weight, Lr is the learning rate, and dw is the derivative of W.
The weight update formula after introducing momentum is as follows:
v
=
m
o
m
e
n
t
u
m
∗
v
−
L
r
∗
d
w
w
=
w
+
v
v= momentum*v - Lr*dw \\w = w + v
v=momentum∗v−Lr∗dww=w+v
Here momentum is momentum and v is velocity. This formula means to add the product of v and momentum last updated. When the direction of this gradient descent - Lr * dw is the same as that of the last update v, the last update v can play a positive acceleration role. When the direction of this gradient descent - Lr * dw is opposite to that of the last update v, the last update v can slow down.
The corresponding codes are as follows:
if momentum != 0:
buf = momentum_buffer_list[i]
if buf is None:
buf = torch.clone(d_p).detach()
momentum_buffer_list[i] = buf
else:
buf.mul_(momentum).add_(d_p, alpha=1 - dampening)
if nesterov:
d_p = d_p.add(buf, alpha=momentum)
else:
d_p = buf
0x04 visualization
4.1 current problems
So far, we still have several unsolved problems, which are underlined below.
-
Build optimizer based on model parameters
-
- It is constructed with optimizer = optim. SGD (parameters = net. Parameters(), LR = 1), so it looks like parameters are assigned to the internal member variables of the optimizer (we assume they are called parameters).
- The model includes two fully connected layers, Linear. How do these layers update parameters???
- weight and bias in Linear are Parameter types.
- Parameter requires in parameter constructor_ grad=True. This setting indicates that the parameter needs to calculate the gradient by default.
- Therefore, Linear weight and bias require the engine to calculate its gradient.
- Of ToyModel_ The parameters member variable is obtained through the parameters method, which returns an Iterator.
- This iterator is used as a parameter to build the SGD optimizer.
- Now the parameters of the SGD optimizer is a pointer to ToyModel_ iterator for parameters. This shows that the optimizer actually optimizes the ToyModel directly_ parameters.
-
-
Engine calculation gradient
- How to ensure that Linear can calculate gradients?
- weight and bias are Parameter types. By default, the gradient needs to be calculated.
- 2) For the model, how does the calculated gradient correspond to the Linear parameter? Where do these gradients calculated by the engine accumulate???
- How to ensure that Linear can calculate gradients?
-
Optimizer optimization parameters:
-
- Call step for optimization. The optimization goal is the internal member variable self.parameters of the optimizer.
- self.parameters is a pointer to ToyModel_ iterator for parameters. This shows that the optimizer actually optimizes the ToyModel directly_ parameters.
-
-
Optimizer update model:
-
- The update of optimization objectives (self.parameters) actually directly affects model parameters (such as Linear).
-
Let's print the outputs and see the next_ Actually, there are three functions. It shows that the previous legend is simplified, and we need to further visualize it.
outputs = {Tensor: 10}
T = {Tensor: 5}
data = {Tensor: 10}
device = {device} cpu
dtype = {dtype} torch.float32
grad = {NoneType} None
grad_fn = {AddmmBackward}
metadata = {dict: 0} {}
next_functions = {tuple: 3}
0 = {tuple: 2} (<AccumulateGrad object at 0x7f9c3e3bd588>, 0)
1 = {tuple: 2} (<ReluBackward0 object at 0x7f9c3e5178d0>, 0)
2 = {tuple: 2} (<TBackward object at 0x7f9c3e517908>, 0)
__len__ = {int} 3
requires_grad = {bool} True
is_cuda = {bool} False
is_leaf = {bool} False
is_meta = {bool} False
is_mkldnn = {bool} False
is_mlc = {bool} False
is_quantized = {bool} False
is_sparse = {bool} False
is_sparse_csr = {bool} False
is_vulkan = {bool} False
is_xpu = {bool} False
layout = {layout} torch.strided
name = {NoneType} None
names = {tuple: 2} (None, None)
ndim = {int} 2
output_nr = {int} 0
requires_grad = {bool} True
4.2 PyTorchViz visualization network
We use PyTorchViz to show the network.
Install library first:
pip install torchviz
Then add code visualization. We use the visualization function make_dot() to get the drawing object. After running, a. gv file and a. png file will be generated in the data folder under the same root directory of the code,. gv file is the script code of the picture generated by Graphviz tool, and. png is the picture generated by compiling the. gv file. By default, the program automatically opens the. png file.
import torch
import torch.nn as nn
import torch.optim as optim
from torchviz import make_dot
class ToyModel(nn.Module):
def __init__(self):
super(ToyModel, self).__init__()
self.net1 = nn.Linear(10, 10)
self.relu = nn.ReLU()
self.net2 = nn.Linear(10, 5)
def forward(self, x):
return self.net2(self.relu(self.net1(x)))
net = ToyModel()
print(net) # Print it by the way
optimizer = optim.SGD(params=net.parameters(), lr = 1)
optimizer.zero_grad()
input = torch.randn(10,10)
outputs = net(input)
outputs.backward(outputs)
optimizer.step()
NetVis = make_dot(outputs, params=dict(list(net.named_parameters()) + [('x', input)]))
NetVis.format = "bmp" # file format
NetVis.directory = "data" # File generated folder
NetVis.view() # Generate file
Output.
ToyModel( (net1): Linear(in_features=10, out_features=10, bias=True) (relu): ReLU() (net2): Linear(in_features=10, out_features=5, bias=True) )
The legend is as follows:

We found that the previous sketch ignored the key link of AccumulateGrad. Let's analyze it next.
0x05 AccumulateGrad
5.1 principle
Let's first give an overview of the relevant principles of PyTorch.
Conceptually, autograd records a calculation diagram. There are two kinds of nodes in the graph: leaf nodes and non leaf nodes.
Nodes created by users are called leaf nodes, for example:
a=torch.tensor([1.0])
The runtime variables are:
a = {Tensor: 1} tensor([1.])
T = {Tensor: 1} tensor([1.])
data = {Tensor: 1} tensor([1.])
device = {device} cpu
dtype = {dtype} torch.float32
grad = {NoneType} None
grad_fn = {NoneType} None
is_cuda = {bool} False
is_leaf = {bool} True
requires_grad = {bool} False
But at this time, a cannot be derived. When creating a tensor, if you set requires_grad is Ture, then pytoch knows that it is necessary to automatically derive the tensor.
a=torch.tensor([1.0], requires_grad = True)
The runtime variables are:
a = {Tensor: 1} tensor([1.], requires_grad=True)
T = {Tensor: 1} tensor([1.], grad_fn=<PermuteBackward>)
data = {Tensor: 1} tensor([1.])
device = {device} cpu
dtype = {dtype} torch.float32
grad = {NoneType} None
grad_fn = {NoneType} None
is_cuda = {bool} False
is_leaf = {bool} True
requires_grad = {bool} True
shape = {Size: 1} 1
PyTorch will record the operation history of each step of the tensor, so as to generate a conceptual directed acyclic graph. The leaf node of the acyclic graph is the input tensor of the model, and its root is the output tensor of the model. The user does not need to code all execution paths of the graph, because what the user runs is what the user wants to differentiate later. By tracking this graph from root to leaf, you can automatically calculate the gradient using chain derivation rules.
In terms of internal implementation, autograd represents this graph as a graph of "Function" or "Node" object (real expression), which can be evaluated using the apply method.
During back propagation, the autograd engine traces the source of the graph from the root node (that is, the output node of forward propagation), so that the gradient of all leaf nodes can be calculated by using the chain derivation rule. Each forward propagation operation function has a back propagation function corresponding to it. This back propagation function is used to calculate the gradient of each variable.
In the back-propagation graph, the back-propagation calculation function corresponding to the leaf node tensor to be derived is AccumulateGrad, and its gradient is cumulative. Multiple derivations will accumulate on the derivative of this tensor, for example:
a=torch.tensor([5.0], requires_grad = True) b = torch.tensor([3.0], requires_grad = True) c = a + b
Corresponding to:
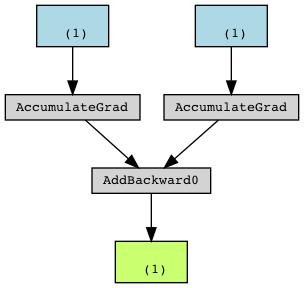
Corresponding to our example, all Linear instances are explicitly defined by the user, and all are leaf nodes.
5.2 AccumulateGrad
5.2.1 definitions
The definition is as follows: accumulateGrad is actually:
- Accumulate the gradient first.
- Then call the incoming update_grad function to update the gradient.
struct TORCH_API AccumulateGrad : public Node {
explicit AccumulateGrad(Variable variable_);
variable_list apply(variable_list&& grads) override;
static at::Tensor callHooks(
const Variable& variable,
at::Tensor new_grad) {
for (auto& hook : impl::hooks(variable)) {
new_grad = (*hook)({new_grad})[0];
}
return new_grad;
}
template <typename T>
static void accumulateGrad(
const Variable& variable,
at::Tensor& variable_grad,
const at::Tensor& new_grad,
size_t num_expected_refs,
const T& update_grad) { // Incoming update gradient function
if (!variable_grad.defined()) {
// ignore
} else if (!GradMode::is_enabled()) {
if (variable_grad.is_sparse() && !new_grad.is_sparse()) {
auto result = new_grad + variable_grad;
update_grad(std::move(result));
} else if (!at::inplaceIsVmapCompatible(variable_grad, new_grad)) {
auto result = variable_grad + new_grad;
update_grad(std::move(result));
} else {
variable_grad += new_grad; // Accumulate
}
} else {
at::Tensor result;
if (variable_grad.is_sparse() && !new_grad.is_sparse()) {
// CPU backend throws an error on sparse + dense, so prefer dense + sparse here.
result = new_grad + variable_grad; // Accumulate
} else {
// Assumes operator+ result typically matches strides of first arg,
// and hopes variable_grad was originally created obeying layout contract.
result = variable_grad + new_grad; // Accumulate
}
update_grad(std::move(result));
}
}
Variable variable;
};
5.2.2 apply
When calling apply, there are two points to note:
- The update function passed in is {grad = std::move(grad_update);} update gradient.
- mutable_grad gets the gradient member variables of the tensor.
Tensor& mutable_grad() const {
return impl_->mutable_grad();
}
/// Accesses the gradient `Variable` of this `Variable`.
Variable& mutable_grad() override {
return grad_;
}
The specific codes are as follows:
auto AccumulateGrad::apply(variable_list&& grads) -> variable_list {
check_input_variables("AccumulateGrad", grads, 1, 0);
if (!grads[0].defined())
return {};
if (variable.grad_fn())
throw std::logic_error(
"leaf variable has been moved into the graph interior");
if (!variable.requires_grad())
return {};
at::Tensor new_grad = callHooks(variable, std::move(grads[0]));
std::lock_guard<std::mutex> lock(mutex_);
at::Tensor& grad = variable.mutable_grad(); // Get mutable of variable_ grad
accumulateGrad(
variable,
grad,
new_grad,
1 + !post_hooks().empty() /* num_expected_refs */,
[&grad](at::Tensor&& grad_update) { grad = std::move(grad_update); });
return variable_list();
}
The specific logic of the flow chart is as follows:
AccumulateGrad Tensor AutogradMeta
+ + +
| | |
| | |
| | |
v | |
apply(update_grad) | |
+ | |
| | |
| | |
| | |
v | |
accumulateGrad | |
+ | |
| | |
| result = variable_grad + new_grad | |
| | |
v result v v
update_grad +----------------------------> mutable_grad +---> grad_
Or as follows, for a leaf tensor, AccumulateGrad will be called for cumulative gradient during reverse calculation, and then updated to the grad of leaf tensor_ in
+----------------------------------------------+ +-------------------------+
|Tensor | |TensorImpl |
| | | |
| | bridge | |
| <TensorImpl, UndefinedTensorImpl> impl_ +-----------> | autograd_meta_ +---------+
| | | | |
| | | | |
+----------------------------------------------+ +-------------------------+ |
|
|
|
+-------------------------+ |
| AutogradMeta | <-----------------------------------------------------------+
| |
| |
| | +------------------------------------------------+
| | | AccumulateGrad |
| grad_fn_ +--------------------> | |
| | | |
| | | apply(grads) { |
| | | |
| grad_accumulator_ | | accumulateGrad(new_grad) { |
| | | |
| | | result = variable_grad + new_grad |
| | update | |
| grad_ <--------------------------------+ update_grad(result) |
| | | |
| | | } |
| | | } |
| | | |
| | | |
+-------------------------+ +------------------------------------------------+
Now we know that the gradient is the grad accumulated at the leaf node_ But how do these gradients update the model parameters?
5.3 combination optimizer
We go back to the step function of SGD, select only the key part, you can see that it obtains the gradient of parameters in the model, and then update the model parameters.
@torch.no_grad()
def step(self, closure=None):
# Recalculate loss using closure
# Update the variable using the calculated gradient
# self.param_groups is the parameter list we passed in
for group in self.param_groups: # Each group is a dict that contains the necessary parameters required for each group of parameters
for p in group['params']: # Traverse all parameters to be updated in this group
if p.grad is not None: # Get the gradient of model parameters
params_with_grad.append(p) # Optimization using gradient
d_p_list.append(p.grad)
# momentum related
F.sgd(params_with_grad, # Update the current group learning parameter w.data -= w.grad*lr, using param.add_(d_p, alpha=-lr) to update the parameters
d_p_list,
momentum_buffer_list,
weight_decay=weight_decay,
momentum=momentum,
lr=lr,
dampening=dampening,
nesterov=nesterov)
# update momentum_buffers in state
return loss
0x06 summary
We summarize it in the order of building optimizer based on model parameters - > engine calculation gradient - > optimizer optimization parameters - > optimizer updating model.
-
Build optimizer based on model parameters
-
- It is constructed with optimizer = optim.SGD(params=net.parameters(), lr = 1), so that params is assigned to the internal member variable param of the optimizer_ Groups.
- The model includes two Linear layers. How do these layers update parameters?
- weight and bias in Linear are Parameter types.
- Parameter requires in parameter constructor_ grad=True. This setting indicates that the parameter needs to calculate the gradient by default.
- Therefore, Linear weight and bias require the engine to calculate its gradient.
- weight, bias is added to the of ToyModel_ parameters member variable.
- Of ToyModel_ The parameters member variable is obtained through the parameters method, which returns an Iterator.
- Use this iterator as a parameter to build the SGD optimizer.
- Now the parameters of the SGD optimizer is a pointer to ToyModel_ iterator for parameters. This shows that the optimizer actually optimizes the ToyModel directly_ parameters.
- Therefore, the optimizer directly optimizes and updates Linear's weight and bias. In fact, the optimizer is just a set of code. What to optimize needs to be specified during construction. It is OK to optimize the parameters of a model and other variables specified by the user.
- weight and bias in Linear are Parameter types.
-
-
Engine calculation gradient
- How to ensure that Linear can calculate gradients?
- weight and bias are Parameter types. By default, the gradient needs to be calculated.
-
- So calculate the weight bias gradient.
- For the model, how does the calculated gradient correspond to the Linear parameter? Where do these gradients calculated by the engine accumulate?
- Corresponding to our example, all Linear instances are explicitly defined by the user, so they are leaf nodes.
-
- The leaf node accumulates the gradient in the model parameter tensor autograd through AccumulateGrad_ meta_. grad_ in
- How to ensure that Linear can calculate gradients?
-
Optimizer optimization parameters:
-
- Call step for optimization. The optimization goal is the internal member variable self.parameters of the optimizer.
- self.parameters is a pointer to ToyModel_ iterator for parameters. This shows that the optimizer actually optimizes the ToyModel directly_ parameters.
-
-
Optimizer update model:
-
- The update of optimization objectives (self.parameters) actually directly affects model parameters (such as Linear weight, bias).
-
See the figure for details:
+---------------------------------------------------------------------+
| ToyModel |
| +---------------------------------+ +------------+ | +------------------+
| | Linear(10, 10) +------> ReLU +-->+Linear(10,5)| | | Engine |
| | | | | |forward / backward | |
| | weight=Parameter | | weight | +-----------------> | Compute gradient |
| | +---------------+ | bias | | | + |
| | +----------------------------+ | | +--+---------+ | | | |
| | | bias=Parameter | | | | | | | |
| | | | | | | | +------------------+
| | | | | | | | 3 accumulate |
| | | autograd_meta_.grad_ <----------------------------------------------------+ 2 | gradient
| | | | | | | | | |
| | | data | | | | | | v
| | | | | v v | |
| | | | | self._parameters | | +------------------+
| | +----------------------------+ | + | | | AccumulateGrad |
| +---------------------------------+ | | | | |
| | | | | |
| v | 5 update -----------+ apply() |
| para_iterator = parameters() <----------------+ | |
| + | | | |
| | | | +------------------+
| | | |
+---------------------------------------------------------------------+ |
1 | |
| |
+---------------------------------------------------------------------------+
| SGD | | |
| | | |
| v + |
| 4 step() |
^-------------> self.param_groups = para_iterator(ToyModel._parameters) +---------------->
| | | |
| | | |
| +---------------------------------------------------------------------------+ |
| |
<--------------------------------------------------------------------------------------+ v
Mobile phones are as follows:
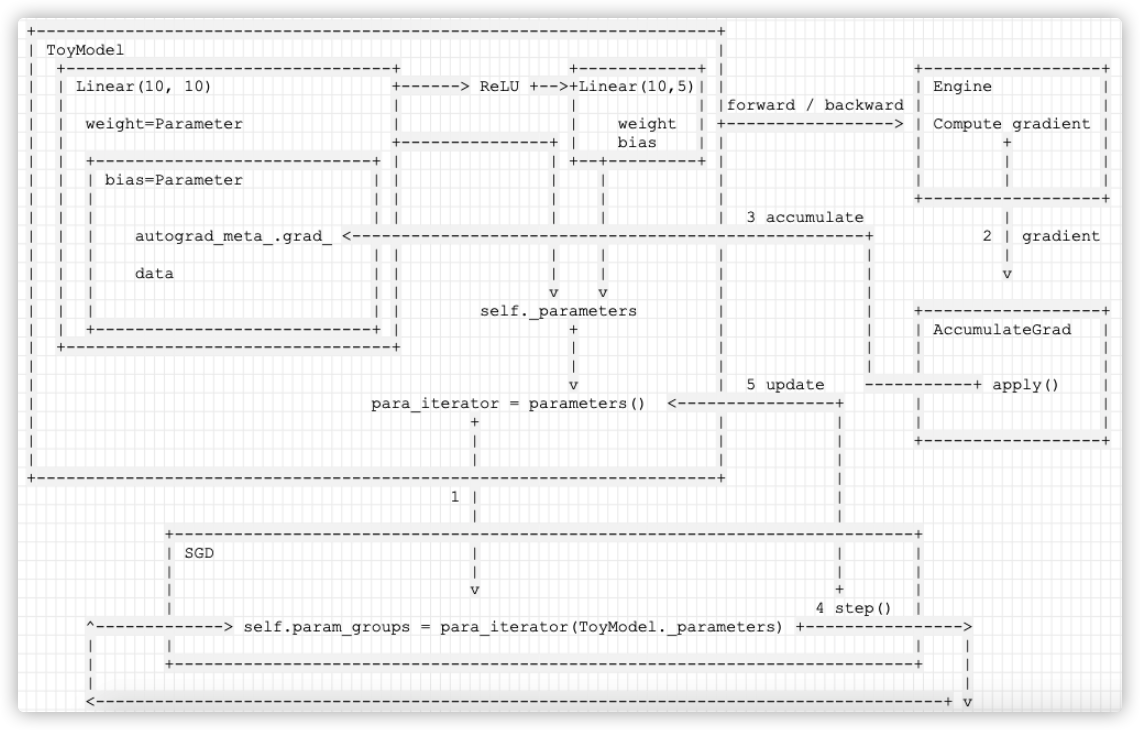
So far, the analysis of the ordinary optimizer is completed. In the next chapter, we will analyze the data parallel optimizer.
0xEE personal information
★★★★★★★ thinking about life and technology ★★★★★★
Wechat public account: Rossi's thinking
If you want to get the news push of personal articles in time, or want to see the technical materials recommended by yourself, please pay attention.

0xFF reference
torch.optim.optimizer source code reading and flexible use
pytorch source code reading (II) optimizer principle
Summary and comparison of various optimization methods (sgd/momentum/Nesterov/adagrad/adadelta)
[optimizer] optimizer algorithm and PyTorch implementation (I): Eternal SGD
Taking optim.SGD as an example, this paper introduces the pytorch optimizer
Pytoch learning notes 08 --- detailed explanation of Optimizer algorithm (SGD, Adam)
Detailed explanation of pytorch optimizer: SGD
addmm() and addmm in pytoch_ Detailed explanation of () usage