17. ST_ClusterWithin

ST_ClusterWithin - aggregation. Returns an array of geometric sets, where each geometric set represents a set of geometric sets, and the distance between geometric sets does not exceed the specified distance.

17.1. Summary

geometry[] ST_ClusterWithin(geometry set g, float8 distance);

17.2. Description

ST_ClusterWithin is an aggregate function that returns an array of geometric sets, where each geometric set represents a set of geometric sets sent no more than a specified distance( Distance is the Cartesian distance in SRID.)

17.3. Example

WITH testdata AS
(SELECT unnest(ARRAY['LINESTRING (0 0, 1 1)'::geometry,
                     'LINESTRING (5 5, 4 4)'::geometry,
                     'LINESTRING (6 6, 7 7)'::geometry,
                     'LINESTRING (0 0, -1 -1)'::geometry,
                     'POLYGON ((0 0, 4 0, 4 4, 0 4, 0 0))'::geometry]) AS geom)
SELECT ST_AsText(unnest(ST_ClusterWithin(geom, 1.4))) FROM testdata;

st_astext
GEOMETRYCOLLECTION(LINESTRING(0 0,1 1),LINESTRING(5 5,4 4),LINESTRING(0 0,-1 -1),POLYGON((0 0,4 0,4 4,0 4,0 0)))
GEOMETRYCOLLECTION(LINESTRING(6 6,7 7))

18. ST_Contains

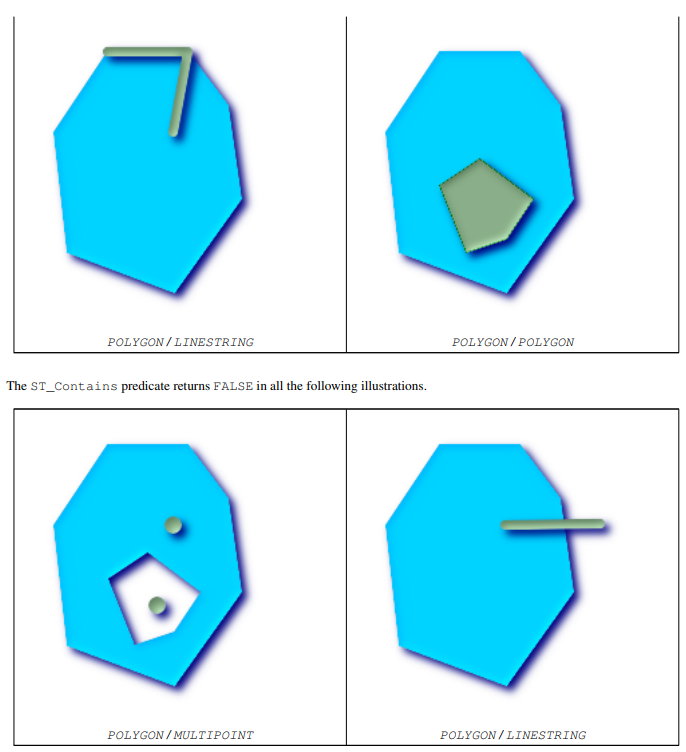
ST_Contains - returns true if and only if B has no points outside A and at least one point inside B is inside A.

18.1. Summary

boolean ST_Contains(geometry geomA, geometry geomB);

18.2. Description

Geometry A contains geometry B if and only if any point of B is not outside A and at least one point inside B is inside A. An important subtlety of this definition is that A does not contain its boundary, but A contains itself. With ST_Contains, in contrast, in St_ In contains, geometry A does not contain itself correctly.

Returns TRUE if geometry B is completely within geometry A. For this function to be meaningful, the source geometry must have the same coordinate projection and the same SRID. ST_Contains is an internal St_ The reciprocal of. Therefore, ST_Contains (A, b) indicates st_ in (B, A), The result is always false, whether defined or not, except in the case of invalid geometry. Performed by GEOS module

• Do not call GEOMETRYCOLLECTION as a parameter
• Do not use this function on invalid geometry. You will get unexpected results.

This function call will automatically include a bounding box comparison that will take advantage of any indexes available on the geometry. To avoid using indexes, use_ ST_Contains function.

• This method implements the OpenGIS simple function implementation specification of SQL 1.1. s2.1.1.2 / / s2.1.13.3 is the same as within(geometry B, geometry A)
• This method implements the SQL/MM specification. SQL-MM 3: 5.1.31

18.3. Example

SELECT ST_Contains(smallc, bigc) As smallcontainsbig,
       ST_Contains(bigc,smallc) As bigcontainssmall,
       ST_Contains(bigc, ST_Union(smallc, bigc)) as bigcontainsunion,
       ST_Equals(bigc, ST_Union(smallc, bigc)) as bigisunion,
       ST_Covers(bigc, ST_ExteriorRing(bigc)) As bigcoversexterior,
       ST_Contains(bigc, ST_ExteriorRing(bigc)) As bigcontainsexterior
FROM (SELECT ST_Buffer(ST_GeomFromText('POINT(1 2)'), 10) As smallc,ST_Buffer(ST_GeomFromText('POINT(1 2)'), 20) As bigc) As foo;

smallcontainsbig	bigcontainssmall	bigcontainsunion	bigisunion	bigcoversexterior	bigcontainsexterior
f	t	t	t	t	f

SELECT ST_GeometryType(geomA) As geomtype, ST_Contains(geomA,geomA) AS acontainsa, 
       ST_ContainsProperly(geomA, geomA) AS acontainspropa,
       ST_Contains(geomA, ST_Boundary(geomA)) As acontainsba, ST_ContainsProperly(geomA,ST_Boundary(geomA)) As acontainspropba
FROM (VALUES ( ST_Buffer(ST_Point(1,1), 5,1) ),( ST_MakeLine(ST_Point(1,1), ST_Point(-1,-1) ) ),( ST_Point(1,1) )) As foo(geomA);

geomtype	acontainsa	acontainspropa	acontainsba	acontainspropba
ST_Polygon	t	f	f	f
ST_LineString	t	f	f	f
ST_Point	t	t	f	f

19. ST_ContainsProperly

ST_ContainsProperly - returns true if B intersects the inside of a instead of the boundary (or outside). A cannot properly contain itself, but it does contain itself.

19.1. Summary

boolean ST_ContainsProperly(geometry geomA, geometry geomB);

19.2. Description

Returns true if B intersects the inside of A instead of the boundary (or outside).
A cannot properly contain itself, but it does contain itself.
Every point in other geometry is a point inside this geometry. ST_ Intersection matrix of two geometrically matched DE-9IM in relate [T**FFFF]

• Rewrite it a little from the JTS document: use this predicate relative to ST_Contains and St_ The advantage of intersects is that it can be calculated effectively without calculating the topology at a single point. An example use case for this predicate is to calculate the intersection of a set of geometry with a large polygon geometry. Since intersection is a rather slow operation, it can more effectively filter out the test geometry completely within the region using containsloper. In these cases, the intersection is known a priori and is accurate to the original test geometry.
• Do not call GEOMETRYCOLLECTION as a parameter
• Do not use this function on invalid geometry. You will get unexpected results.

This function call will automatically include a bounding box comparison that will take advantage of any indexes available on the geometry. To avoid using indexes, use_ st_ Containshopper function.

19.3. Example

SELECT ST_ContainsProperly(smallc, bigc) As smallcontainspropbig,
       ST_ContainsProperly(bigc,smallc) As bigcontainspropsmall,
       ST_ContainsProperly(bigc, ST_Union(smallc, bigc)) as bigcontainspropunion,
       ST_Equals(bigc, ST_Union(smallc, bigc)) as bigisunion,
       ST_Covers(bigc, ST_ExteriorRing(bigc)) As bigcoversexterior,
       ST_ContainsProperly(bigc, ST_ExteriorRing(bigc)) As bigcontainsexterior
FROM (SELECT ST_Buffer(ST_GeomFromText('POINT(1 2)'), 10) As smallc,ST_Buffer(ST_GeomFromText('POINT(1 2)'), 20) As bigc) As foo;

smallcontainspropbig	bigcontainspropsmall	bigcontainspropunion	bigisunion	bigcoversexterior	bigcontainsexterior
f	t	f	t	t	f

SELECT ST_GeometryType(geomA) As geomtype, 
       ST_Contains(geomA,geomA) AS acontainsa, 
       ST_ContainsProperly(geomA, geomA) AS acontainspropa,
       ST_Contains(geomA, ST_Boundary(geomA)) As acontainsba, 
       ST_ContainsProperly(geomA, ST_Boundary(geomA)) As acontainspropba
FROM (VALUES ( ST_Buffer(ST_Point(1,1), 5,1) ),( ST_MakeLine(ST_Point(1,1), ST_Point(-1,-1) ) ),( ST_Point(1,1) )) As foo(geomA);

geomtype	acontainsa	acontainspropa	acontainsba	acontainspropba
ST_Polygon	t	f	f	f
ST_LineString	t	f	f	f
ST_Point	t	t	f	f

20. ST_Covers

ST_Covers - returns 1 (TRUE) if no point in geometry B is outside geometry A

20.1. Summary

boolean ST_Covers(geometry geomA, geometry geomB);
boolean ST_Covers(geography geogpolyA, geography geogpointB);

20.2. Description

Returns 1 (TRUE) if no point in Geometry/Geography B is outside of Geometry/Geography A
Performed by GEOS module

• Do not call GEOMETRYCOLLECTION as a parameter
• Do not use this function on invalid geometry. You will get unexpected results.

This function call will automatically include a bounding box comparison that will take advantage of any indexes available on the geometry. To avoid using indexes, use_ ST_Covers function.

Note: This is the "allowed" version and returns Boolean values instead of integers.

Not OGC standard, but Oracle also has.

ST_Contains and St_ Some of the subtleties of within are not intuitively obvious. For details, please refer to OGC cover, contents and internal subtleties

20.3. Example

SELECT ST_Covers(smallc,smallc) As smallinsmall,
       ST_Covers(smallc, bigc) As smallcoversbig,
       ST_Covers(bigc, ST_ExteriorRing(bigc)) As bigcoversexterior,
       ST_Contains(bigc, ST_ExteriorRing(bigc)) As bigcontainsexterior
FROM (SELECT ST_Buffer(ST_GeomFromText('POINT(1 2)'), 10) As smallc,
             ST_Buffer(ST_GeomFromText('POINT(1 2)'), 20) As bigc) As foo;

smallinsmall	smallcoversbig	bigcoversexterior	bigcontainsexterior
t	f	t	f

SELECT ST_Covers(geog_poly, geog_pt) As poly_covers_pt,
       ST_Covers(ST_Buffer(geog_pt,10), geog_pt) As buff_10m_covers_cent
FROM (SELECT  ST_Buffer(ST_GeogFromText('SRID=4326;POINT(-99.327 31.4821)'), 300) As geog_poly,
              ST_GeogFromText('SRID=4326;POINT(-99.33 31.483)') As geog_pt ) As foo;

poly_covers_pt	buff_10m_covers_cent
f	t

21. ST_CoveredBy

ST_CoveredBy - returns 1 (TRUE) if no point in Geometry/Geography A is outside Geometry/Geography B

21.1. Summary

boolean ST_CoveredBy(geometry geomA, geometry geomB);
boolean ST_CoveredBy(geography geogA, geography geogB);

21.2. Description

Returns 1 (TRUE) if no point in Geometry/Geography A is outside Geometry/Geography B
Performed by GEOS module

• Do not call GEOMETRYCOLLECTION as a parameter
• Do not use this function on invalid geometry. You will get unexpected results.

This function call will automatically include a bounding box comparison that will take advantage of any indexes available on the geometry. To avoid using indexes, use_ ST_CoveredBy function.
Note: This is the "allowed" version and returns Boolean values instead of integers.
Not OGC standard, but Oracle also has.
ST_Contains and St_ Some of the subtleties of within are not intuitively obvious. For details, see supplements of OGC covers, contains, within

21.3. Example

SELECT ST_CoveredBy(smallc,smallc) As smallinsmall,
       ST_CoveredBy(smallc, bigc) As smallcoveredbybig,
       ST_CoveredBy(ST_ExteriorRing(bigc), bigc) As exteriorcoveredbybig,
       ST_Within(ST_ExteriorRing(bigc),bigc) As exeriorwithinbig
FROM (SELECT  ST_Buffer(ST_GeomFromText('POINT(1 2)'), 10) As smallc,
              ST_Buffer(ST_GeomFromText('POINT(1 2)'), 20) As bigc) As foo;

smallinsmall	smallcoveredbybig	exteriorcoveredbybig	exeriorwithinbig
t	t	t	f

22. ST_Crosses

ST_Crosses - returns TRUE if the geometry provided has some (but not all) internal common points.

22.1. Summary

boolean ST_Crosses(geometry g1, geometry g2);

22.2. Description

ST_Crosses accepts two geometric objects. If their intersection is "spatial cross", that is, there are some but not all internal points in the geometry, it returns TRUE. The intersection within the geometry cannot be an empty set, and its dimension must be less than the maximum dimension of the two input geometry. In addition, the intersection of two geometries must not be equal to either source geometry. Otherwise, FALSE is returned.
In mathematical terms, this means:

a . C r o s s e s ( b ) = ( d i m ( I ( a ) ∩ I ( b ) ) < m a x ( d i m ( I ( a ) , I ( b ) ) ) ) a.Crosses(b)=(dim(I(a) \cap I(b)) < max(dim(I(a),I(b)))) a.Crosses(b)=(dim(I(a)∩I(b))<max(dim(I(a),I(b))))
[ a ∩ b ≠ a a \cap b \neq a a∩b​=a,
a ∩ b ≠ b a \cap b \neq b a∩b​=b]

The DE-9IM intersection matrix of the two geometries is:

   T*T****** (Apply to point/Line and point/Areas and lines/Regional situation)
   T*****T** (For line/Point and area/Points and areas/Line condition)
   0******** (Line/Line condition)

This predicate returns false for any other dimension combination.
OpenGIS simple functional specification defines this predicate only for point / line, point / area, line / line and line / area. JTS / GEOS extends this definition to line / point, area / point and area / line. This makes the relationship symmetrical.

• Do not call GEOMETRYCOLLECTION as a parameter
• Do not use this function on invalid geometry. You will get unexpected results.

22.3. Example

-- Consider a case where the user has two tables:One is the road table and the other is the highway table. 

CREATE TABLE roads (
       id serial NOT NULL,
       the_geom geometry,
       CONSTRAINT roads_pkey PRIMARY KEY ( road_id)
);

CREATE TABLE highways (
       id serial NOT NULL,
       the_gem geometry,
       CONSTRAINT roads_pkey PRIMARY KEY ( road_id)
);

-- To determine the list of roads crossing the highway, you can use a query similar to the following:  

SELECT roads.id 
FROM roads, highways 
WHERE ST_Crosses(roads.the_geom, highways.the_geom);

23. ST_LineCrossingDirection

ST_LineCrossingDirection - given 2 line strings, a number between - 3 and 3 is returned to indicate which cross behavior. 0 is disjoint.

23.1. Summary

integer ST_LineCrossingDirection(geometry linestringA, geometry linestringB);

23.2. Description

Given two line strings, a number between - 3 and 3 is returned to indicate which crossover behavior. 0 is disjoint. This only supports LINESTRING
Integer constants are defined as follows:

• 0: LINE NO CROSS no cross
• -1: LINE CROSS LEFT
• 1: LINE CROSS RIGHT
• -2: LINE MULTICROSS END LEFT
• 2: LINE MULTICROSS END RIGHT
• -3: LINE MULTICROSS END SAME FIRST LEFT
• 3: LINE MULTICROSS END SAME FIRST RIGHT

23.3. Example

• Line 1 (green), line 2 (blue), the ball is the starting point and the triangle is the end point. The following is the query.

SELECT ST_LineCrossingDirection(foo.line1 , foo.line2) As l1_cross_l2 ,
       ST_LineCrossingDirection(foo. line2, foo.line1) As l2_cross_l1
FROM (SELECT ST_GeomFromText('LINESTRING(25 169,89 114,40 70,86 43)') As line1,
             ST_GeomFromText('LINESTRING(171 154,20 140,71 74,161 53)') As line2 ) As foo;

l1_cross_l2	l2_cross_l1
3	-3

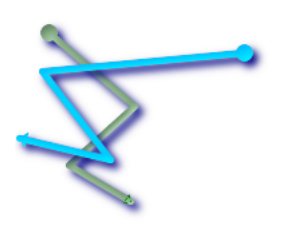
• Line 1 (green), line 2 (blue), the ball is the starting point and the triangle is the end point. The following is the query.

SELECT ST_LineCrossingDirection(foo.line1 , foo.line2) As l1_cross_l2 ,
       ST_LineCrossingDirection(foo.line2, foo.line1) As l2_cross_l1
FROM (SELECT ST_GeomFromText('LINESTRING(25 169,89 114,40 70,86 43)') As line1,
             ST_GeomFromText('LINESTRING (171 154, 20 140, 71 74, 2.99 90.16)') As line2) As foo;

l1_cross_l2	l2_cross_l1
2	-2

• Line 1 (green), line 2 (blue), the ball is the starting point and the triangle is the end point. The following is the query.

SELECT ST_LineCrossingDirection(foo.line1, foo.line2) As l1_cross_l2 ,
       ST_LineCrossingDirection(foo.line2, foo.line1) As l2_cross_l1
FROM (SELECT ST_GeomFromText('LINESTRING(25 169,89 114,40 70,86 43)') As line1,
             ST_GeomFromText('LINESTRING (20 140, 71 74, 161 53)') As line2 ) As foo;

l1_cross_l2	l2_cross_l1
-1	1

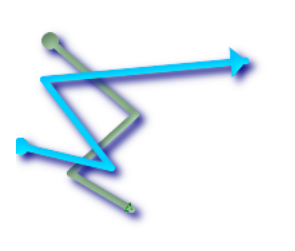
• Line 1 (green), line 2 (blue), the ball is the starting point and the triangle is the end point. The following is the query.

SELECT ST_LineCrossingDirection(foo.line1 , foo.line2) As l1_cross_l2 ,
       ST_LineCrossingDirection(foo.line2, foo.line1) As l2_cross_l1
FROM (SELECT ST_GeomFromText('LINESTRING(25 169,89 114,40 70,86 43)') As line1,
             ST_GeomFromText('LINESTRING(2.99 90.16,71 74,20 140,171 154)') As line2) As foo;

l1_cross_l2	l2_cross_l1
-2	2

SELECT s1.gid, s2.gid, ST_LineCrossingDirection(s1.the_geom, s2.the_geom)
FROM streets s1 CROSS JOIN streets s2 ON (s1.gid != s2.gid AND s1.the_geom && s2.the_geom )
WHERE ST_CrossingDirection(s1.the_geom, s2.the_geom) > 0;

24. ST_Disjoint

ST_Disjoint - returns TRUE if the geometry does not Spatially Intersect, if they do not share any space together.

24.1. Summary

boolean ST_Disjoint(geometry A ,geometry B);

24.2. Description

Overlaps, Touches, Within all geometries are not disjoint in space. If any of the above returns true, the geometry is not spatially disjoint. Disjoint indicates that the space intersection is false.

• Do not call GEOMETRYCOLLECTION as a parameter

Performed by GEOS module

• This function call does not use an index
• Note: This is the "allowed" version and returns Boolean values instead of integers.

24.3. Example

SELECT ST_Disjoint('POINT(0 0)'::geometry, 'LINESTRING (2 0, 0 2)'::geometry);

st_disjoint
t

SELECT ST_Disjoint('POINT(0 0)'::geometry, 'LINESTRING ( 0 0, 0 2 )'::geometry);

st_disjoint
f

25. ST_Distance

ST_Distance - for geometry types, returns the 2D Cartesian distance between two geometries in projected units (based on the spatial reference system). For geographic types, the default is to return the minimum geodesic distance between two geographic locations, in meters.

25.1. Summary

float ST_Distance(geometry g1, geometry g2);
float ST_Distance(geography gg1, geography gg2);
float ST_Distance(geography gg1, geography gg2, boolean use_spheroid);

25.2. Description

For geometry type, returns the minimum 2D Cartesian distance between two geometries in projected units (spatial reference units). For the geography type, the default is to return the minimum geodesic distance between two geographic locations, in meters. If use_ If spheroid is false, a faster sphere calculation is used instead of an ellipsoid.

• This method implements the OpenGIS simple function implementation specification of SQL 1.1.
• This method implements the SQL/MM specification. SQL-MM 3: 5.1.23
• This method supports circular strings and curves
• The SFCGAL backend also provides this method.

25.3. Example

-- Coordinate conversion returns length units=degree

SELECT ST_Distance(
              'SRID=4326;POINT(-72.1235 42.3521)'::geometry,
              'SRID=4326;LINESTRING(-72.1260 42.45, -72.123 42.1546)'::geometry);

st_distance
0.00150567726382282

-- Coordinate conversion returns length units=rice

SELECT ST_Distance(
              ST_Transform('SRID=4326;POINT(-72.1235 42.3521)'::geometry, 3857),
              ST_Transform('SRID=4326;LINESTRING(-72.1260 42.45, -72.123 42.1546)'::geometry, 3857));

st_distance
167.441410065196

-- Use latitude to correct coordinate conversion errors
SELECT ST_Distance(
              ST_Transform('SRID=4326;POINT(-72.1235 42.3521)'::geometry, 3857),
              ST_Transform('SRID=4326;LINESTRING(-72.1260 42.45, -72.123 42.1546)'::geometry, 3857)) * cosd(42.3521);

st_distance
123.742351254151

-- Geometric example-In meters(SRID: 26986 Massachusetts flat meter)(Most accurate)
SELECT ST_Distance(
              ST_Transform('SRID=4326;POINT(-72.1235 42.3521)'::geometry, 26986),
              ST_Transform('SRID=4326;LINESTRING(-72.1260 42.45, -72.123 42.1546)'::geometry, 26986));

st_distance
123.797937878454

-- Geometry example-Unit: M(SRID: 2163 National Atlas of the United States)(Least accurate)  
SELECT ST_Distance(
              ST_Transform('SRID=4326;POINT(-72.1235 42.3521)'::geometry, 2163),
              ST_Transform('SRID=4326;LINESTRING(-72.1260 42.45, -72.123 42.1546)'::geometry, 2163));

st_distance
126.664256056812

-- Same as the geometric example, but pay attention to the unit of meter-Using the sphere is slightly faster and less accurate  
SELECT ST_Distance(gg1, gg2) As spheroid_dist, ST_Distance(gg1, gg2, false) As sphere_dist
FROM (SELECT 'SRID=4326;POINT(-72.1235 42.3521)'::geography as gg1,
             'SRID=4326;LINESTRING(-72.1260 42.45, -72.123 42.1546)'::geography as gg2
) As foo ;

spheroid_dist	sphere_dist
123.802076746848	123.475736916397