Previous remarks

HZ people seem to have learnt Splay, and the lecturers often say Splay, so do the gods of our school.

Every time they say Splay, I say that I won't be too embarrassed. After learning Splay, I really feel that it is a very beautiful data structure.

Summary

Pre-cheese: Binary Search Tree

A binary sorting tree is either an empty tree or a binary tree with the following properties:
If the left subtree is not empty, the value of all nodes in the left subtree is less than or equal to the value of its root node; if the right subtree is not empty, the value of all nodes in the right subtree is greater than or equal to the value of its root node; and the left subtree and the right subtree are binary sorting trees, respectively.
The same sequence, because of different sorting, may generate different binary sorting trees, search efficiency is not necessarily the same. If the binary sorting tree degenerates into a chain, the efficiency is very low.
(The above is copied)

Notice the last sentence, and a bunch of balance trees emerge to improve the efficiency of BST and avoid the problem of BST degenerating into chains.

GMK told me Treap was useless, so I learned Splay first.(

Various operations

Splay is an optimized BST that adjusts itself through stretching operations to improve efficiency.

First of all, we have to look at a rotation operation, which is the basis of the extension operation.

rotate

Look at this tree. It doesn't roar.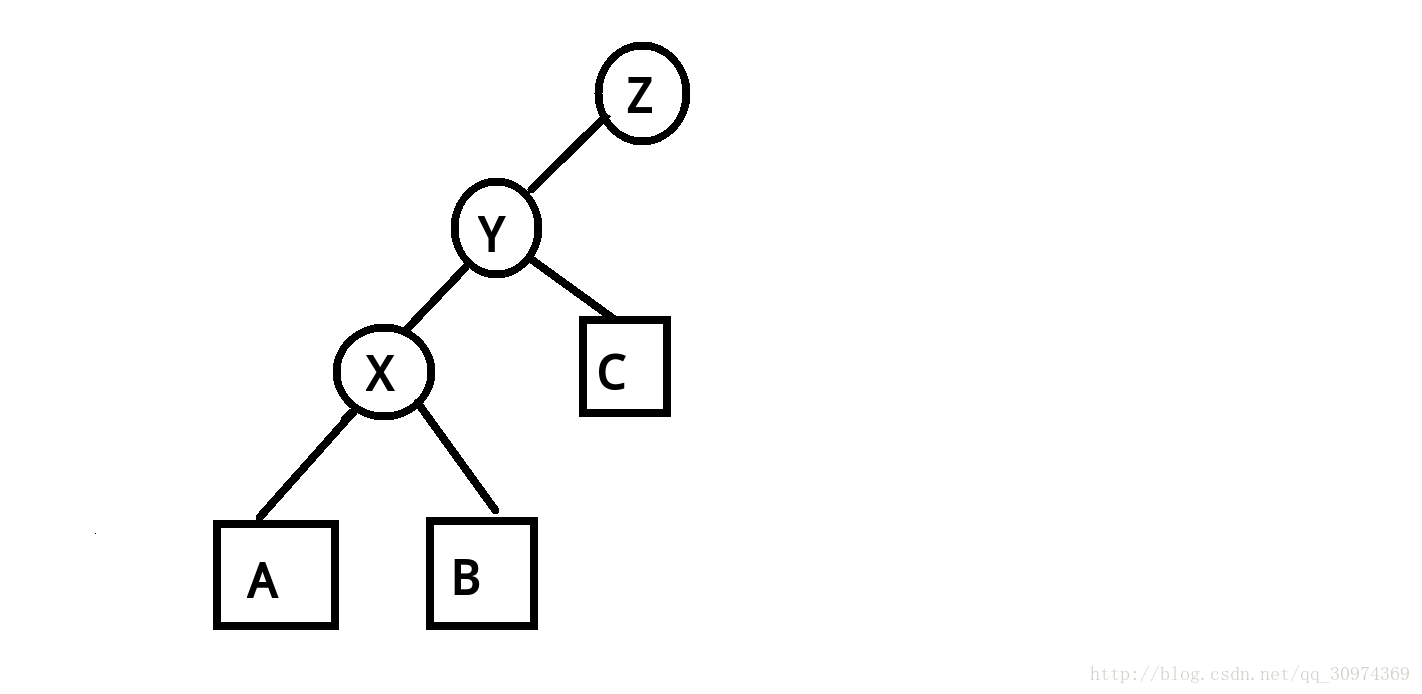

Pictures are stolen

No yelling! It's too long and inefficient. So we can turn x to y and reconstruct the structure of the tree to make the depth of the tree better.

How can rotation not change BST properties?

First, Y > x, so y should be placed in the right subtree of X. Then connect x to z. Y is short of a left son (which it had), X has a previous right son, and this right son must be less than y, so the right son of X is replaced by the left son of Y.

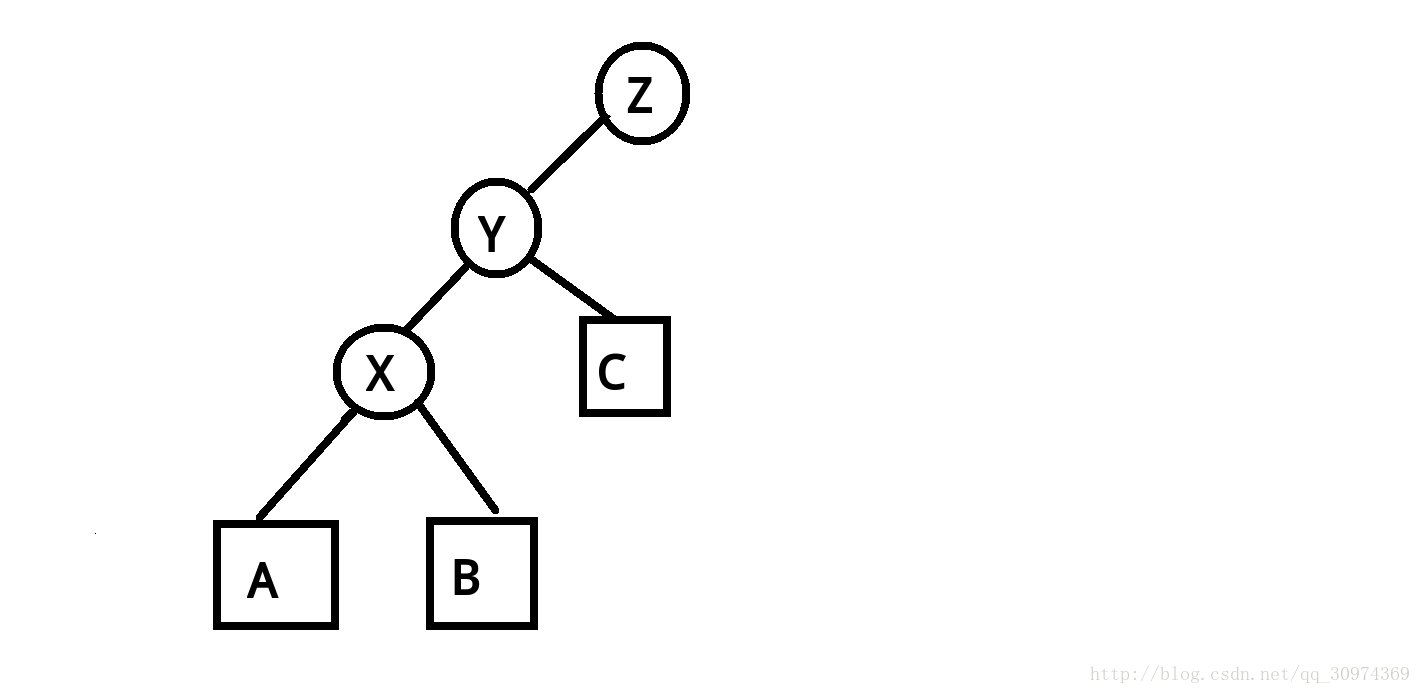
To be continued...

Template: [LOJ 104. General Balance Tree]( https://loj.ac/problem/104)

#include <bits/stdc++.h>

const int N = 3e5 + 233, INF = 0x3f3f3f3f;
int n;

struct Splay {
    int root, tot, ch[N][2], siz[N], cnt[N], fa[N], val[N];
    Splay() {
        root = 1, ch[1][1] = 2;
        val[1] = -INF, val[2] = INF;
        cnt[1] = cnt[2] = 1;
        siz[1] = siz[2] = 1;
        fa[2] = 1, tot = 2;
    }
    inline int get(int x) { return ch[fa[x]][1] == x; }
    void update(int x) { siz[x] = siz[ch[x][0]] + siz[ch[x][1]] + cnt[x]; }
    void rotate(int x) {
        int f1 = fa[x], f2 = fa[f1], id = get(x);
        ch[f1][id] = ch[x][id ^ 1], fa[ch[f1][id]] = f1;
        ch[f2][get(f1)] = x, fa[x] = f2;
        ch[x][id ^ 1] = f1, fa[f1] = x;
        update(f1);
    }
    void splay(int x, int goal = 0) {
        while (fa[x] != goal) {
            int f1 = fa[x], f2 = fa[f1];
            if (f2 != goal) {
                if (get(x) == get(f1))
                    rotate(f1);
                else
                    rotate(x);
            }
            rotate(x);
        }
        update(x);
        if (!goal)
            root = x;
    }
    void find(int x) {
        int p = root;
        while (ch[p][x > val[p]] && x != val[p]) p = ch[p][x > val[p]];
        splay(p);
    }
    void insert(int x) {
        int cur = root, p = 0;
        while (cur && val[cur] != x) p = cur, cur = ch[cur][x > val[cur]];
        if (cur)
            ++cnt[cur];
        else {
            cur = ++tot;
            if (p)
                ch[p][x > val[p]] = cur;
            ch[cur][0] = ch[cur][1] = 0;
            val[cur] = x, fa[cur] = p;
            cnt[cur] = siz[cur] = 1;
        }
        splay(cur);
    }
    int get_pre(int x) {
        find(x);
        if (val[root] < x)
            return root;
        int p = ch[root][0];
        while (ch[p][1]) p = ch[p][1];
        return p;
    }
    int get_nxt(int x) {
        find(x);
        if (val[root] > x)
            return root;
        int p = ch[root][1];
        while (ch[p][0]) p = ch[p][0];
        return p;
    }
    void remove(int x) {
        int pre = get_pre(x), nxt = get_nxt(x);
        splay(pre), splay(nxt, pre);
        int del = ch[nxt][0];
        if (cnt[del] > 1)
            --cnt[del], splay(del);
        else
            ch[nxt][0] = 0;
    }
    int get_kth(int k) {
        int p = root;
        while (1) {
            if (ch[p][0] && k <= siz[ch[p][0]])
                p = ch[p][0];
            else if (k > siz[ch[p][0]] + cnt[p])
                k -= siz[ch[p][0]] + cnt[p], p = ch[p][1];
            else
                return p;
        }
        return 0;
    }
} splay;

signed main() {
    scanf("%d", &n);
    for (int i = 1, opt, x; i <= n; i++) {
        scanf("%d%d", &opt, &x);
        switch (opt) {
            case 1:
                splay.insert(x);
                break;
            case 2:
                splay.remove(x);
                break;
            case 3:
                splay.find(x);
                printf("%d\n", splay.siz[splay.ch[splay.root][0]]);
                break;
            case 4:
                printf("%d\n", splay.val[splay.get_kth(x + 1)]);
                break;
            case 5:
                printf("%d\n", splay.val[splay.get_pre(x)]);
                break;
            case 6:
                printf("%d\n", splay.val[splay.get_nxt(x)]);
                break;
        }
    }
    return 0;
}