According to the problem solution summary of code Capriccio

thinking

This topic involves two key issues:
1. How to cut
2. Judge whether palindrome

In fact, the cutting problem is similar to the combinatorial problem. So we need to use backtracking to cut strings.

For example, for the string abcdef:

Combinatorial problem: after selecting an a, select the second one in bcdef, select b, and then select the third one in cdef.
Cutting problem: after cutting an a, cut the second segment in bcdef, and then cut the third segment in cdef.

Therefore, the cutting problem can also be abstracted into a tree structure, as shown in the figure:

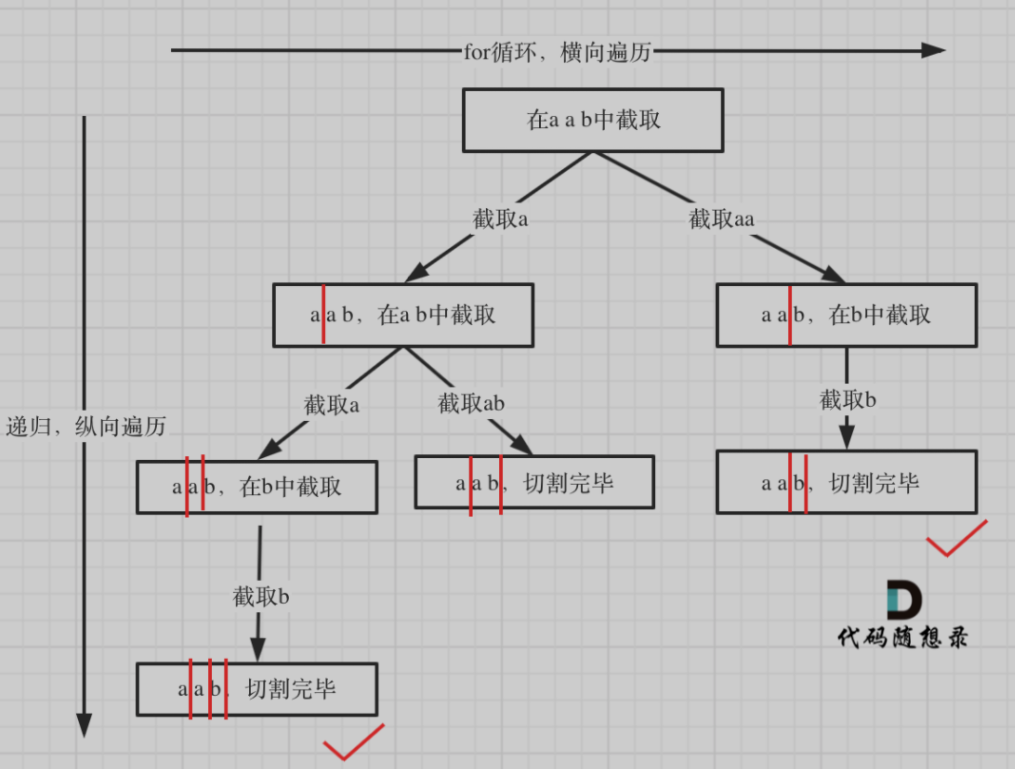
Recursion is used to traverse vertically, for loop is used to traverse horizontally, and the cutting line (that is, the red line in the figure) is cut to the end of the string, indicating that a cutting method has been found.

At this time, it can be found that the backtracking search process of cutting problem is similar to that of combinatorial problem

Cut string

Retrospective Trilogy
Recursive function parameters
The global variable array path stores the substring of the palindrome after cutting, and the two-dimensional array result stores the result set.
startIndex is also required, because the cut places cannot be cut repeatedly, which is consistent with the combination problem.

vector<vector<string>> result;
vector<string> path; // Put the substring of palindromes
void backtracking (const string& s, int startIndex) {

Recursive function termination condition
As can be seen from the above figure, the cutting line startIndex cuts to the end of the string, indicating that a cutting method has been found. At this time, it is the termination condition of recursion in this layer.

void backtracking (const string& s, int startIndex) {
    // If the starting position is greater than or equal to the size of s, a group of segmentation schemes have been found
    if (startIndex >= s.size()) {
        result.push_back(path);
        return;
    }
}

Logic of single layer search
In for (int i = startIndex; I < s.size(); In the I + +) loop, we define the start position startIndex, so [startIndex, i] is the substring to be intercepted.

First, judge whether the substring is a palindrome. If it is a palindrome, add it to the vector path, which is used to record the cut palindrome substring.

for (int i = startIndex; i < s.size(); i++) {
    if (isPalindrome(s, startIndex, i)) { // Is a palindrome substring
        // Get the substring of [startIndex,i] in s
        string str = s.substr(startIndex, i - startIndex + 1);
        path.push_back(str);
    } else {                // If not, skip directly
        continue;
    }
    backtracking(s, i + 1); // Find the substring with i+1 as the starting position
    path.pop_back();        // In the backtracking process, the substring that has been filled in this time will pop up
}

Determine palindrome substring

Determine whether a string is a palindrome.

You can use the double finger needle method. A pointer is from front to back and a pointer is from back to front. If the elements pointed to by the front and back pointers are equal, it is a palindrome string.

 bool isPalindrome(const string& s, int start, int end) {
     for (int i = start, j = end; i < j; i++, j--) {
         if (s[i] != s[j]) {
             return false;
         }
     }
     return true;
 }

class Solution {
public:
    bool isPalindrome(int start,int end,string &s){
        for(;start<end;start++,end--){
            if(s[start]!=s[end]) return false;
        }
        return true;
    }
    vector<vector<string>>res;
    vector<string> path; // Put the substring of palindromes
    void backtracking(string &s,int startIndex){
        if(startIndex>=s.size()){  // If the starting position is larger than the size of s, it indicates that a group of segmentation schemes have been found
            res.push_back(path);
            return;
        }
        for(int ii=startIndex;ii<s.size();ii++){
            string s1=s.substr(startIndex,ii-startIndex+1);// Get the substring of [startIndex,i] in s

            if(isPalindrome(0,s1.size()-1,s1)==true){// Is a palindrome substring
                path.push_back(s1);
            }else continue;  // Not palindromes, skip
            backtracking(s,ii+1);// Find the substring with i+1 as the starting position

            path.pop_back();
        }
    }
    vector<vector<string>> partition(string s) {
        backtracking(s,0);
        return res;
    }
};

Difficulties in this topic:
Cutting problem can be abstracted as combinatorial problem
How to simulate those cutting lines
How to terminate recursion in cutting problem
How to intercept substring in recursive loop
How to judge palindromes