catalogue
4.1} implement stack with two queues
4.2 implementing stack with a queue
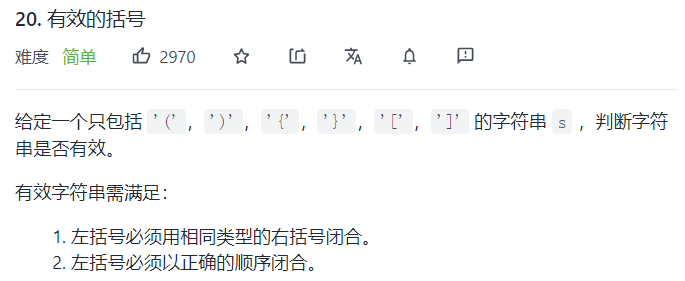
1, Bracket matching problem
The title is described as follows:
Solution idea: use the stack to solve the problem. Scan the string. When the left bracket is encountered, directly enter the stack. When the right bracket is scanned, pop up the top element of the stack to check whether it matches. If not, directly false. Otherwise, repeat the above process.
Two boundary problems:
- After scanning the string, if the stack is not empty, it indicates that there are too many left parentheses and no matching right parentheses. It is directly false.
- When scanning the first right parenthesis, it is found that the stack is empty, indicating that the right parenthesis is the first character of the string, and there is no matching left parenthesis. It is directly false.
The code is as follows:
public class Num20 {
public boolean isValid(String s) {
Stack<Character> stack=new Stack<>();
for (int i = 0; i < s.length(); i++) {
char c=s.charAt(i);
//Left bracket stack
if(c=='{'||c=='['||c=='('){
stack.push(c);
}else{
//When the stack is empty, the description has only right parentheses
if(stack.isEmpty()){
return false;
}
//Left bracket out of stack
char top=stack.pop();
if(c==')'&&top!='('){
return false;
}
if (c==']'&&top!='['){
return false;
}
if(c=='}'&&top!='{'){
return false;
}
}
}
//There are extra left parentheses in the stack
if(!stack.isEmpty()){
return false;
}else {
return true;
}
}
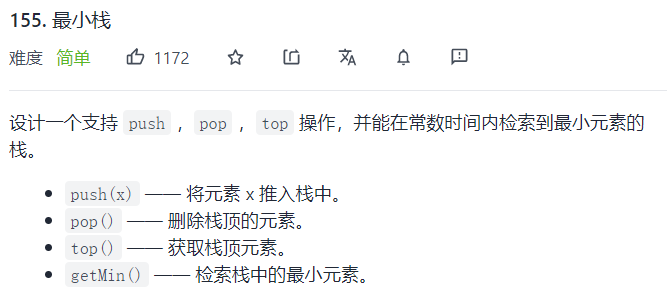
}2, Implement a minimum stack
The title is described as follows:
Solution idea: use double stack to solve the problem, where s1 is the stack that actually stores elements and s2 is the stack that stores the current minimum value. When elements are stacked, s1 is stacked in turn. When s2 is stacked, it is necessary to compare the stacked elements with the current stack top element. If the current stacked element is smaller than the stack top element, put the current stacked element into the stack, otherwise put the current stack top element into the stack again, So getMin() -- just take the stack top element of s2 directly.
The code is as follows:
public class MinStack {
//Stack s1 of actual storage elements
private Stack<Integer> s1=new Stack<>();
//Stack s2 for storing minimum value
private Stack<Integer> s2=new Stack<>();
public MinStack() {}
public void push(int val) {
//Put val into s1 stack first
s1.push(val);
//Judge whether s2 is empty. When it is empty, val will also be put into s2 stack
if(s2.isEmpty()){
s2.push(val);
}else{
//If it is not empty, judge the size of val and s2 stack top elements. If val is smaller, enter val, otherwise continue to enter s2 stack top elements
if(val<s2.peek()){
s2.push(val);
}else{
s2.push(s2.peek());
}
}
}
public void pop() {
//Delete the stack top element, s1 and s2 should be deleted
s1.pop();
s2.pop();
}
public int top() {
//Take out the top element of the stack
return s1.peek();
}
public int getMin() {
//The smallest element only needs to remove the s2 stack top element
return s2.peek();
}
}3, Implement queue with stack
The title is described as follows:

Solution idea: use two stacks to solve the problem. s1 is the stack for actually storing elements and s2 is the auxiliary stack. Each time you add an element, you must ensure that s1 is empty, so that the new element is just at the bottom of the stack.

The code is as follows:
public class MyQueue {
//s1 is used to store elements
private Stack<Integer> s1=new Stack<>();
//s2 is used as an aid
private Stack<Integer> s2=new Stack<>();
public MyQueue() {
}
public void push(int x) {
//Judge whether s1 is empty. When it is empty, add a new element directly. At this time, x is at the bottom of s1 stack
if(s1.isEmpty()){
s1.push(x);
}else{
//When s1 is not empty, all elements in s1 are sequentially stacked in s2
while(!s1.isEmpty()){
int y=s1.pop();
s2.push(y);
}
//At this time, s1 is empty, and then add a new element to s1. At this time, x is at the bottom of the stack of s1
s1.push(x);
//Pop up the elements in s2 again and then enter s1 stack
while(!s2.isEmpty()){
int z=s2.pop();
s1.push(z);
}
}
}
public int pop() {
return s1.pop();
}
public int peek() {
return s1.peek();
}
public boolean empty() {
return s1.isEmpty();
}
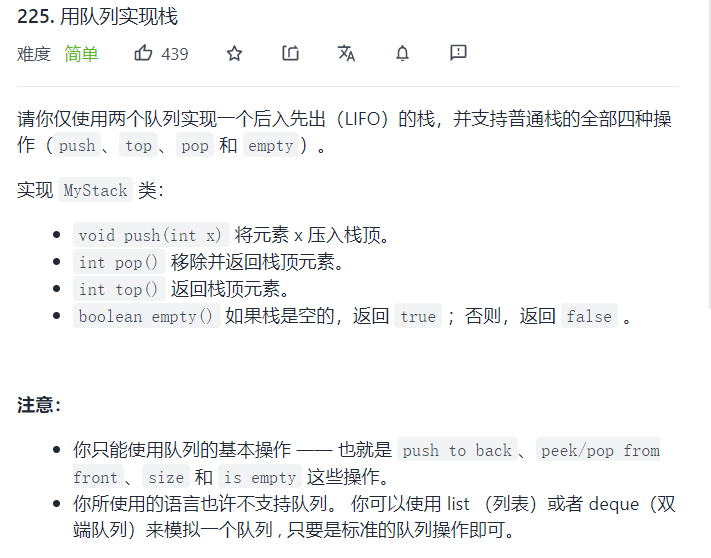
}4, Implement stack with queue
4.1} implement stack with two queues
The title is described as follows:
Problem solving idea: use two queues to solve the problem. q1 is the queue that actually stores elements, and q2 is the auxiliary queue. Ensure that q2 is always empty after adding elements (new elements enter q2 directly), and ensure that new elements are at the end of the queue.

The code is as follows:
public class MyStack {
//q1 is used to store elements
private Queue<Integer> q1=new LinkedList<>();
//q2 is always empty as an auxiliary
private Queue<Integer> q2=new LinkedList<>();
public MyStack() {
}
public void push(int x) {
//The new element joins the team, and at this time, the new element is at the head of the q2 team
q2.offer(x);
//When q1 is not empty, the elements in q1 are dequeued into q2
while(!q1.isEmpty()){
q2.offer(q1.poll());
}
//At this time, q1 is empty and q2 is the queue of storage elements. Exchange the points of q1 and q2. At this time, q2 is empty
Queue<Integer> tmp=q1;
q1=q2;
q2=tmp;
}
public int pop() {
return q1.poll();
}
public int top() {
return q1.peek();
}
public boolean empty() {
return q1.isEmpty();
}
}4.2 implementing stack with a queue
Problem solving idea: first join the team, then take the previous elements out of the team in turn (ensure that the new elements are at the end of the team), and then join the team in turn.
The code is as follows:
public class MyStackⅡ {
private Queue<Integer> queue=new LinkedList<>();
public void push(int x){
//Number of record elements
int size=queue.size();
//Add new elements to the team
queue.offer(x);
//Take the previous elements out of the team and then into the team
for (int i = 0; i < size; i++) {
queue.offer(queue.poll());
}
}
public int pop(){
return queue.poll();
}
public int top(){
return queue.peek();
}
public boolean empty(){
return queue.isEmpty();
}
}5, Design cyclic queue
The title is described as follows:

The code is as follows:
/**
* Design cyclic queue
*/
public class MyCircularQueue {
//Points to the queue head element of the circular queue
private int head;
//End of queue element pointing to a circular queue
private int tail;
//Array of actual storage elements
private int[] data;
public MyCircularQueue(int k) {
//k+1 is because it wastes a space to judge whether the queue is full
this.data=new int[k+1];
}
public boolean enQueue(int value) {
if (isFull()){
return false;
}else{
data[tail]=value;
tail=(tail+1)%data.length;
return true;
}
}
public boolean deQueue() {
if (isEmpty()){
return false;
}else{
head=(head+1)%data.length;
return true;
}
}
public int Front() {
if (isEmpty()){
return -1;
}else{
return data[head];
}
}
public int Rear() {
if (isEmpty()){
return -1;
}else{
//Gets the index of the last element
int lastIndex=(tail==0?data.length-1:tail-1);
return data[lastIndex];
}
}
public boolean isEmpty() {
return head==tail;
}
public boolean isFull() {
return (tail+1)%data.length==head;
}
}6, Next larger element
The title is described as follows:

Solution idea: use the monotone stack to solve the problem and maintain a monotone increasing stack (the elements from the top of the stack to the bottom of the stack increase in turn). This problem can only look at nums2. Look backwards from the last element of nums2 to the right, find the next larger element of each element in nums2, and traverse nums2. When the traversal element is larger than the element at the top of the stack, Go out of the stack until the top element is larger than the current element or the stack is empty. When the stack is empty, return - 1, indicating that there is no element at the top of the current stack that is larger than the current element.
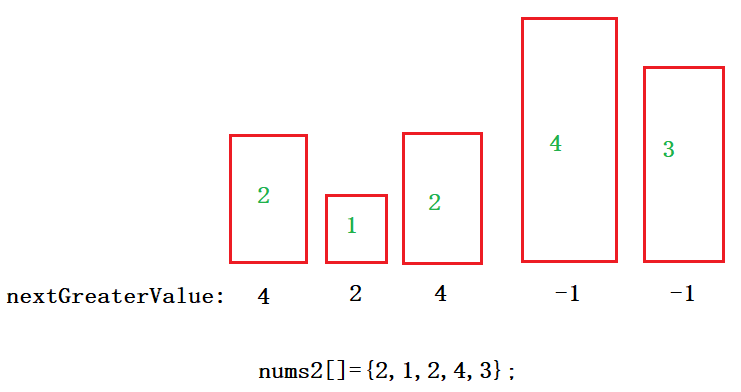
The code is as follows:
/**
* The monotone stack solves the next larger element problem
*/
public class Num496_nextGreaterElement {
//Monotone stack
private Stack<Integer> stack=new Stack<>();
//Store each element in nums2 and their next larger element
private Map<Integer,Integer> map=new HashMap<>();
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
//Scan nums2 to find the next larger element of each element in nums2
for (int i = nums2.length-1; i >=0 ; i--) {
//When the stack is empty and the top element of the stack is smaller than the current element, the elements in the stack are out of the stack,
// Until the top element of the stack is larger than the current element or the stack is empty
while(!stack.isEmpty()&&stack.peek()<=nums2[i]){
stack.pop();
}
int nextGreaterValue=stack.isEmpty()?-1:stack.peek();
//After processing the current element, push the current element onto the stack
stack.push(nums2[i]);
map.put(nums2[i],nextGreaterValue);
}
//Scan nums1 and take out the nextGreaterValue corresponding to each element
int[] ret=new int[nums1.length];
for (int i = 0; i < nums1.length; i++) {
ret[i]=map.get(nums1[i]);
}
return ret;
}
}