Title Description: define the data structure of the stack. Please implement a min function that can get the smallest element of the stack in this type. In this stack, the time complexity of calling min, push and pop is O(1).

Problem solving ideas: push and pop methods belong to the basic methods in the stack; The min and top methods return the data in the stack without modifying the contents of the stack.

min method: if you need to output a minimum value, you need to compare all the values in the stack, and if you need to compare, you need to get it; After getting the traversal comparison, the original stack structure will be destroyed, and another stack is needed for intermediate operation. (own understanding)

Important ideas in the answer: 1) learned a new method peek() to return the top element of the stack;

2) To get the time complexity of O(1), you need to use the method peek. When entering the stack, always put the smallest element on the top of the auxiliary stack, and use peek to get O(1);

3) It is necessary to use less than or equal to ensure that the number of minimum values stored in stack2 is equal to the number of minimum values stored in stack1;

4) The stack top element in stack2 is always the minimum value in stack1. The pop operation of stack1 needs to judge whether to pop the minimum element in the stack: if so, pop the minimum element in stack2 at the same time, but there will never be less than the stack top element in stack1;

5) You need to use the equals method to judge the same situation, because = = only judges the address value of Integer class. It is easy to see that the specific values are the same but do not belong to the same address, so there is no pop in stack2, resulting in a wrong answer! As follows:

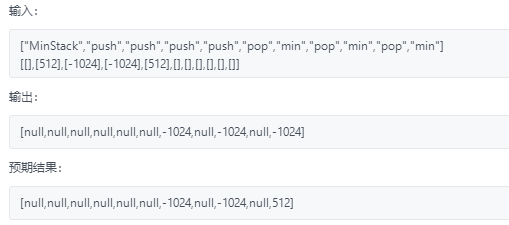
This involves a cache problem. The Integer class will have a cache pool in [- 128127]. At this time, you can use = = to judge whether the values are equal. Beyond this range, a new object will be created, and then = =. If the values are equal, false will be returned because the address is compared

public static Integer valueOf(int i) {
        if (i >= IntegerCache.low && i <= IntegerCache.high)
            return IntegerCache.cache[i + (-IntegerCache.low)];
        return new Integer(i);
}

6) pop, push and peek are all o(1) time complexity methods

Handwritten code: the time complexity of O(1) is beyond the time limit

pop the data in stack1 one by one and compare them; At the same time, the data is stored in the stack2 intermediate container
Then the data stored in stack2 is returned to stack1, which has a great time complexity

Time complexity needs to be further understood

class MinStack {

    private Stack stack1;
    private Stack stack2;
   
    public MinStack() {
        this.stack1 = new Stack<Integer>();
        this.stack2 = new Stack<Integer>();
    }
    
    public void push(int x) {
       stack1.push(x);
    }
    
    public void pop() {
        stack1.pop();
    }
    
    public int top() {
        int i = (int)stack1.pop();
        stack1.push(i);
        return i;
    }
    
    //Only output without popping the data in the container
    //pop the data in stack1 one by one and compare them; At the same time, the data is stored in the stack2 intermediate container
    //Then the data stored in stack2 is returned to stack1, which has a great time complexity
    public int min() {
        int i = top();
        while(!stack1.isEmpty()){
            int j = (int)stack1.pop();
            stack2.push(j);
            if(i > j) {
                i = j;
            }
        }
        while(!stack2.isEmpty()){
            int k = (int)stack2.pop();
            stack1.push(k);
        }
        return i;
    }
}

Answer code: learned a new function peek(); Return the top element of the stack!

Code modified according to the answer:

class MinStack {

    private Stack stack1;
    private Stack stack2;

    public MinStack() {
        this.stack1 = new Stack<Integer>();
        this.stack2 = new Stack<Integer>();
    }
    
    //When the element is put into the stack, the smallest element is always placed at the top of the auxiliary stack.
    public void push(int x) {
       stack1.push(x);
       if(stack2.isEmpty() || (x <= (int)stack2.peek())){
           stack2.push(x);
       }
    }
    
    //At this time, when pop in stack1, judge whether to take out the smallest element in the stack. If it is the smallest element, pop the top of stack 2 at the same time;
    //When entering the stack, the number of minimum values stored in stack2 and the number of minimum values in stack1 need to be the same. At this time, it is judged by less than or equal to
    public void pop() {
        if(stack1.pop().equals(stack2.peek())){
            stack2.pop();
        }
    }
    
    public int top() {
        return (int)stack1.peek();
    }
    
    public int min() {
        return (int)stack2.peek();
    }
}