preface
My story with topological sorting
The first contact was the class of data structure. However, I was addicted to playing games and didn't understand the code at that time. The second time was the punch in group. The second question of a force deduction fortnightly competition was topological sorting (I used violence to cycle 100 times and hash to rewrite). The group leader found that the topological sorting of group members was not good enough to write topological topics. Y total array simulation data structure, I read or not ah 🤣 I can't write for two consecutive days and lose 20 yuan. I still can't y always write arrays 🤣.
Later, during the winter vacation, the group began to punch in and conducted a special training on topological sorting for a period of time. (thanks to the group leader, although he can't see it)
The following is a summary of konjaku's experience in realizing topological sorting with STL.
What scenario is topology sorting applicable to
The premise must be a directed acyclic graph. The meaning of the question is related to converting the graph into linear sorting
Template
Directly on the STL version. Array simulation will be updated after understanding
//Firmly grasp the node with penetration of 0 is regarded as the starting point of a new round
while(q.size())
{
//The one-way relationship between m and edge hash table edge storage nodes
string tmp = q.front(); q.pop();
for(auto &i : m[tmp]) //Reduce the penetration of all nodes that the node can reach by one
{
edge[i] --;
if(edge[i] == 0) //If the penetration of the node becomes 0, it will be regarded as a new starting point
{
q.push(i);
ans.push_back(i);
}
}
}
For example, click the title jump link
I Find all the dishes that can be made from a given raw material
The source is a two-week race, which is the first topological ranking I have come into contact with in my impression. It's of great significance, so I put it in the first one.
1. Title
You have information about n different dishes. Give you a string array recipes and a two-dimensional string array ingredients. The name of dish I is recipes[i]. If you have all its raw materials ingredients[i], you can make this dish. The raw material of one dish may be another dish, that is, ingredients[i] may contain another string in recipes.
At the same time, give you a string array supplies, which contains all the raw materials you have at the beginning. You have unlimited quantities of each raw material.
Please return to all the dishes you can make. You can return them in any order.
Note that the two dishes may contain each other in their raw materials.
Example 1: Input: recipes = ["bread"], ingredients = [["yeast","flour"]], supplies = ["yeast","flour","corn"] Output:["bread"] Explanation: We can make "bread" ,Because we have raw materials "yeast" and "flour" . Example 2: Input: recipes = ["bread","sandwich"], ingredients = [["yeast","flour"],["bread","meat"]], supplies = ["yeast","flour","meat"] Output:["bread","sandwich"] Explanation: We can make "bread" ,Because we have raw materials "yeast" and "flour" . We can make "sandwich" ,Because we have raw materials "meat" And can make raw materials "bread" . Example 3: Input: recipes = ["bread","sandwich","burger"], ingredients = [["yeast","flour"],["bread","meat"],["sandwich","meat","bread"]], supplies = ["yeast","flour","meat"] Output:["bread","sandwich","burger"] Explanation: We can make "bread" ,Because we have raw materials "yeast" and "flour" . We can make "sandwich" ,Because we have raw materials "meat" And can make raw materials "bread" . We can make "burger" ,Because we have raw materials "meat" And can make raw materials "bread" and "sandwich" . Example 4: Input: recipes = ["bread"], ingredients = [["yeast","flour"]], supplies = ["yeast"] Output:[] Explanation: We can't make any dishes because we only have raw materials "yeast" .
Tips:
n == recipes.length == ingredients.length 1 <= n <= 100 1 <= ingredients[i].length, supplies.length <= 100 1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10 recipes[i], ingredients[i][j] and supplies[k] Contains only lowercase English letters. All recipes and supplies The values in are different from each other. ingredients[i] Strings in are different from each other.
2. Analyze the meaning of the question
-
If the raw materials point to the dishes, the topic becomes a "directed acyclic graph" (why does the raw materials point to the dishes? Think about it: only with the ingredients can we make the dishes)
-
Count the penetration of all dishes. When the penetration is 0, dishes become raw materials
-
Establish the relationship between raw materials and vegetables
3. Reference source code
class Solution {
public:
vector<string> findAllRecipes(vector<string>& recipes, vector<vector<string>>& ingredients, vector<string>& supplies) {
//Those with 0 degree are regarded as dishes
unordered_map<string, int> edge; //Storage degree
unordered_map<string, vector<string>> m; //Edge preserving relationship
int n = recipes.size();
for(int i = 0; i < n; ++ i)
{
edge[recipes[i]] += ingredients[i].size(); //Food penetration
for(auto & j : ingredients[i]) m[j].push_back(recipes[i]);
}
vector<string> ans;
queue<string> q;
for(auto &i : supplies) q.push(i);
//Firmly grasp the node with penetration of 0 is regarded as the starting point of a new round
while(q.size())
{
//The one-way relationship between m and edge hash table edge storage nodes
string tmp = q.front(); q.pop();
for(auto &i : m[tmp]) //Reduce the penetration of all nodes that the node can reach by one
{
edge[i] --;
if(edge[i] == 0) //If the penetration of the node becomes 0, it will be regarded as a new starting point
{
q.push(i);
ans.push_back(i);
}
}
}
return ans;
}
};
II Topological sequence directed graph
1. Title
Given a directed graph with n points and m edges, the number of points is 1 to N, and there may be multiple edges and self rings in the graph.
Please output any topological sequence of the directed graph. If the topological sequence does not exist, output − 1.
If A sequence A composed of all points in A graph satisfies that for each edge (x,y), X appears before y in A, then A is A topological sequence of the graph.
Input format
The first line contains two integers n and m.
Next m lines, each containing two integers x and y, indicate that there is a directed edge (x,y) from point x to point y.
Output format
A total of one line. If there is a topological sequence, any legal topological sequence can be output.
Otherwise, output − 1.
Data range
1 ≤ n , m ≤ 1 0 5 1≤n,m≤10^5 1≤n,m≤105
Input sample:
3 3 1 2 2 3 1 3
Output example:
1 2 3
2. Topic analysis
Naked topological sorting problem. Using topological sorting to deal with a graph, what kind of situation is there a ring? The number of nodes in the queue is less than the total number of nodes
3. Reference code
#include <bits/stdc++.h>
using namespace std;
string topsort(unordered_map<int, int> &edge, unordered_map<int, vector<int>> &w, int n)
{
for(int i = 1; i <= n; ++ i) edge[i];
string ans;
queue<int> q;
for(auto &[x, y] : edge)
if(!y)
{
q.push(x); //The with a penetration of 0 is regarded as the starting point
ans += to_string(x); ans += " ";
}
//Still that sentence, firmly grasp the node with penetration of 0 as the starting point
int sum = q.size();
while(q.size())
{
int f = q.front(); q.pop();
for(auto i : w[f])
{
-- edge[i];
if(!edge[i])
{
q.push(i);
sum ++;
ans += to_string(i); ans += " ";
}
}
}
if(n != sum) return "-1"; //When the number of nodes in the queue is less than the total number, there must be a ring
return ans;
}
int main()
{
ios::sync_with_stdio(false);
int n, m; cin >> n >> m;
unordered_map<int, int> edge; //Input degree
unordered_map<int, vector<int>> w; //Edge relationship
int x, y;
for(int i = 0; i < m; ++ i) //Don't worry about duplication
{
cin >> x >> y;
edge[y] ++;
w[x].push_back(y);
}
cout << topsort(edge, w, n);
return 0;
}
III Topological order
Idea: a point with a penetration of 0 is regarded as the starting point. If the penetration of a point is not 0 and appears first, it must not be topological sorting.
Naked questions. Don't repeat the question
Reference code
#include <bits/stdc++.h>
using namespace std;
bool check(vector<int> &a, unordered_map<int, int> &edge, unordered_map<int, vector<int>> &w)
{
unordered_map<int, int> g = edge;
for(int &i : a)
{
for(int &j : w[i])
-- g[j];
if(g[i]) return false; //Nodes with a penetration greater than 1 are not topological sorting
}
return true;
}
int main()
{
ios::sync_with_stdio(false);
int n, m; cin >> n >> m;
unordered_map<int, int> edge;//degree
unordered_map<int, vector<int>> w;//edge
//Create a relationship between degree and edge
int x, y;
for(int i = 0; i < m; ++ i)
{
cin >> x >> y;
edge[y] ++;
w[x].push_back(y);
}
int T; cin >> T;
for(int i = 0; i < T; ++ i)
{
vector<int> a(n);
for(int i = 0; i < n; ++ i) cin >> a[i];
if(!check(a, edge, w)) cout << i << ' ';
}
return 0;
}
IV food chain
1. Title
As shown in the figure is a schematic diagram of the food web of an ecosystem. Answer this question according to the figure.
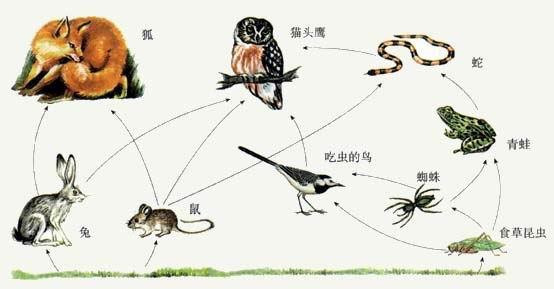
Now give you n species and m energy flow relationships, and find the number of food chains.
The names of species are numbered from 1 to n. The m-Bar energy flow relationship is as follows:
a1 b1
a2 b2
a3 b3
...
am−1 bm−1
am bm
ai bi indicates that energy flows from species ai to species bi. Note that a single isolated organism is not a food chain.
Input format
The first line contains two integers n and m. Next, there are two integers AI and Bi in each line of M lines to describe m energy flow relationships.
The data guarantees the biological characteristics of the input data symbol, and there will be no repeated energy flow relationship.
Output format
An integer, that is, the number of food chains in the food web.
Data range
1
≤
n
≤
1
0
5
,
0
≤
m
≤
2
×
1
0
5
,
1≤n≤10^5,0≤m≤2×10^5,
1≤n≤105,0≤m≤2×105,
Make sure the answer is in the int range.
Input sample:
10 16 1 2 1 4 1 10 2 3 2 5 4 3 4 5 4 8 6 5 7 6 7 9 8 5 9 8 10 6 10 7 10 9
Output example:
9
2. Topic analysis
-
Still topological sorting. The node with an exit of 0 is the end point
-
Number of regular board plus array records
-
An isolated organism alone is not a food chain. Therefore, the summation should be calculated in the nodes that are not in the team for the first time, the entry degree is reduced to 0, and there is no exit degree
3. Reference code
#include <bits/stdc++.h>
using namespace std;
int topsort(unordered_map<int, int> &edge, unordered_map<int, vector<int>> &w,
unordered_map<int, int> &sum, vector<bool> &b, int n)
{
int ans = 0;
queue<int> q;
for(auto &[x, y] : edge)
if(!y)
{
q.push(x);
sum[x] = 1;
}
while(q.size())
{
int f = q.front(); q.pop();
for(auto &i : w[f])
{
-- edge[i];
sum[i] += sum[f];
if(!edge[i]) //An isolated organism alone is not a food chain.
{
q.push(i);
if(!b[i]) ans += sum[i];
}
}
}
return ans;
}
int main()
{
ios::sync_with_stdio(false);
vector<bool> b;
unordered_map<int, int> edge, sum; //Number of degree chains
unordered_map<int, vector<int>> w;
int n, m; cin >> n >> m;
b.resize(n + 1);
for(int i = 1; i <= n; ++ i) edge[i];
int x, y;
for(int i = 0; i < m; ++ i)
{
cin >> x >> y;
edge[y] ++;
w[x].push_back(y);
b[x] = true; //The end point is the one with out degree and the one without out degree
}
cout << topsort(edge, w, sum, b, n);
return 0;
}