This article is from Li Mingzi's csdn blog( http://blog.csdn.net/free1985 For commercial reprints, please contact the blogger for authorization. For non-commercial reprints, please indicate the source.
Abstract: this paper introduces the implementation of plsql-based code storage in the first root traversal tree with layer number. The code in this paper is written in March 2014. In addition, this paper provides the storage process source code and sample examples of test table creation statement, insertion node, acquisition of direct child node, acquisition of self and descendant node, acquisition of path from root to designated node, deletion node and so on.

1 Storage Mode Introduction

The main idea of the storage method of the first root traversal tree with layer number is to maintain the hierarchical relationship of the tree structure by recording the sequence number of the first visit to the node in the first root traversal (hereinafter referred to as the left value) and the order number of the second visit in the backtracking (hereinafter referred to as the right value). From the concept of root traversal, we can see that the left value of the child node must be greater than the left value of the parent node, and the right value must be less than the right value of the parent node. Combined with sorting operation, it is easy to query tree data without recursion. In addition, on the basis of recording the left and right values, the method also maintains the layer number of the node to reduce the time complexity of querying the direct (parent) child nodes.
The storage structure of the first root traversal tree with layer numbers is shown in Table 1-1.

Table 1-1 Storage structure of first-root traversal tree with layer number

2 tabular statement

The table building statement of the first root traversal tree with layer number under Oracle is as follows.

CREATE TABLE TREE
(
    NODENAME   NVARCHAR2(50) NOT NULL, 
    LEVELNUM  NUMBER(8) NOT NULL, 
    LEFTVALUE   NUMBER(8) NOT NULL, 
    RIGHTVALUE  NUMBER(8) NOT NULL );

COMMENT ON TABLE TREE IS 'Traversal Tree with Layer First Root'
;
COMMENT ON COLUMN TREE.NODENAME   IS 'Node name'
;
COMMENT ON COLUMN TREE.LEVELNUM  IS 'Layer number, starting from 1'
;
COMMENT ON COLUMN TREE.LEFTVALUE   IS 'First root traversal left value'
;
COMMENT ON COLUMN TREE.RIGHTVALUE  IS 'First root traversal right value'
;

ALTER TABLE TREE ADD CONSTRAINT PK_NODENAME
    PRIMARY KEY (NODENAME)
;

3 Insert Node

3.1 Implementation
The insertion node stored procedure code is as follows:

procedure InsertNode --Insert Node
  (parentName in nvarchar2, --Parent node name, empty when inserting root
   nodeName  in nvarchar2 --Node name
   ) is
    parentRight TREE.RIGHTVALUE%type; --Right value of parent node
    parentLevel TREE.LEVELNUM%type; --Parent node hierarchy
  begin
    if parentName is null then
      insert into TREE values (nodeName, 1, 1, 2);
    else
      --Get the right value of the parent node
      select RIGHTVALUE, LEVELNUM
        into parentRight, parentLevel
        from TREE
       where NODENAME = parentName;
      update TREE
         set LEFTVALUE = LEFTVALUE + 2
       where LEFTVALUE > parentRight - 1;
      update TREE
         set RIGHTVALUE = RIGHTVALUE + 2
       where RIGHTVALUE > parentRight - 1;
      insert into TREE
      values
        (nodeName, parentLevel + 1, parentRight, parentRight + 1);
    end if;
  end InsertNode;

3.2 Test
For example, we want to create a tree as shown in Figure 3-1.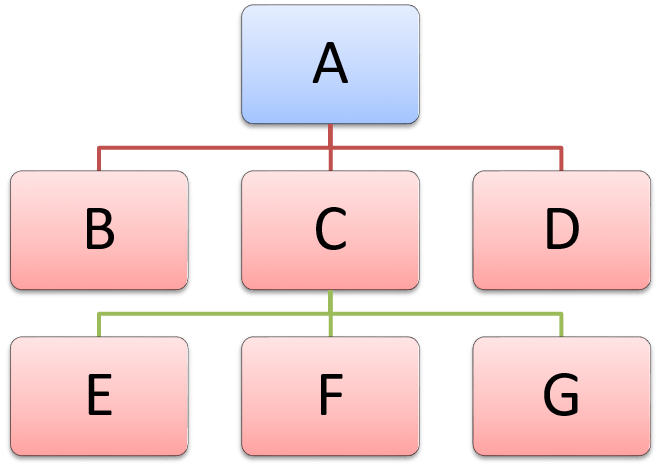

Figure 3-1 Test Case Tree Structure Diagram

To create the tree above, you can call the following sample code:

begin  
-- Call the procedure  
tree_package.InsertNode('', 'A');  
tree_package.InsertNode('A', 'B');  
tree_package.InsertNode('A', 'C');  
tree_package.InsertNode('A', 'D');  
tree_package.InsertNode('C', 'E');  
tree_package.InsertNode('C', 'F');  
tree_package.InsertNode('C', 'G');  
end;  

After executing the test code, the table record is updated to the state shown in Table 3-1.

Table 3-1 Table records after insertion of nodes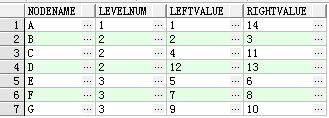

4 Get direct subnodes

4.1 Implementation
Get the direct child stored procedure code as follows:

procedure GetChildren --Get child nodes
  (parentName IN NVARCHAR2, --Parent Node Name
   children  OUT RETCURSOR --Child node name
   ) is
    parentLeft  TREE.LEFTVALUE%type; --Left value of parent node
    parentRight TREE.RIGHTVALUE%type; --Right value of parent node
    parentLevel TREE.LEVELNUM%type;
  begin
    select LEFTVALUE, RIGHTVALUE, LEVELNUM
      into parentLeft, parentRight, parentLevel
      from TREE
     where NODENAME = parentName;
    open children for
      select NODENAME
        from TREE
       where LEFTVALUE between parentLeft and parentRight
         and LEVELNUM = parentLevel + 1
       order by LEFTVALUE asc;
  end GetChildren;

4.2 Test
For example, we want to get the direct child node of node A and call GetChildren to get the cursor as shown in Table 4-1.

Table 4-1 Gets the result cursor of the direct child node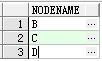

5 Get the current node and descendant node

5.1 Implementation
Get the stored procedure code for the current node and its descendants as follows:

  procedure GetDescendants --Getting descendant nodes
  (parentName IN NVARCHAR2, --Parent Node Name
   descendants  OUT RETCURSOR --Descendant node name
   )is
    parentLeft  TREE.LEFTVALUE%type; --Left value of parent node
    parentRight TREE.RIGHTVALUE%type; --Right value of parent node
  begin
    select LEFTVALUE, RIGHTVALUE
      into parentLeft, parentRight
      from TREE
     where NODENAME = parentName;
    open descendants for
      select NODENAME
        from TREE
       where LEFTVALUE between parentLeft and parentRight
       order by LEFTVALUE asc;
  end GetDescendants;

5.2 Test
For example, if we want to get node A and its descendants and call GetDescendants, we get the cursor as shown in Table 5-1.

Table 5-1 Gets the result cursor for the current node and its descendants

6 Gets the path from the root to the specified node

6.1 Implementation
Get the path stored procedure code from the root to the specified node as follows:

 procedure GetNodePath --Get the node path
  (node IN NVARCHAR2, --Node name
   nodePath OUT RETCURSOR --Node Path
   ) is
    nodeLeft  TREE.LEFTVALUE%type; --Node Left Value
    nodeRight TREE.RIGHTVALUE%type; --Right Value of Node
  begin
    select LEFTVALUE, RIGHTVALUE
      into nodeLeft, nodeRight
      from TREE
     where NODENAME = node;
    open nodePath for
      select NODENAME
        from TREE
       where LEFTVALUE <= nodeLeft
         and RIGHTVALUE >= nodeRight
       order by LEFTVALUE asc;
  end GetNodePath;

6.2 Test
For example, if we want to get the path from root to node G and call GetNodePath, the cursor we get is shown in Table 6-1.

Table 6-1 Returns Result Cursor from Root to Designated Node

7 Delete Nodes

7.1 Implementation
The stored procedure code for deleting nodes is as follows:

procedure DeleteNode --Delete nodes and their children
  (node IN NVARCHAR2 --Node name
   ) is
    nodeLeft     TREE.LEFTVALUE%type; --Node Left Value
    nodeRight    TREE.RIGHTVALUE%type; --Right Value of Node
    delNodeCount NUMBER; --Deleted Nodes
  begin
    select LEFTVALUE, RIGHTVALUE
      into nodeLeft, nodeRight
      from TREE
     where NODENAME = node;
    delNodeCount := (nodeRight - nodeLeft+1)/2;
    delete from TREE
     where LEFTVALUE >= nodeLeft
       and RIGHTVALUE <= nodeRight;
    update TREE
       set LEFTVALUE = LEFTVALUE - delNodeCount * 2
     where LEFTVALUE > nodeLeft;
    update TREE
       set RIGHTVALUE = RIGHTVALUE - delNodeCount * 2
     where RIGHTVALUE > nodeRight;
  end DeleteNode;

7.2 Test
For example, if we want to delete node C, the sub-nodes E, F and G of C will be deleted together. The deleted table record status is shown in Table 7-1.

Table 7-1 Table records after deleting nodes