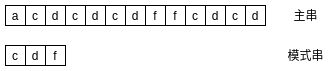
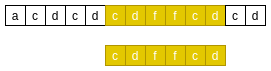
First agree on two concepts, main string and pattern string

For example, if you look up the s string in the s string, s is the main string and S is the mode string

Search the "cdf" mode string in the main string as follows:

Main string and mode string

BF

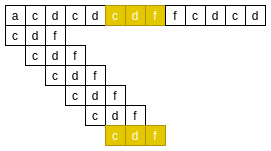
Brute force matching is a very simple string matching algorithm, which matches the characters in the main string with the characters of the pattern string one by one. If a mismatched character pair is encountered, the main string slides back one character and matches from the beginning:

Violent matching

The code implementation is as follows. The function of strStr is to find the location of the first occurrence of the need string from the haystack string. If it is not found, it returns - 1 (LC.28)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

int strStr(string haystack, string needle) { if (needle.empty()) return 0; int sh = haystack.size(); int sn = needle.size(); if (sh < sn) return -1; for (int i = 0; i <= (sh - sn); i++) { int j = 0; for (; j < sn; j++) { if (haystack[i + j] != needle[j]) { break; } } if (j >= sn) { return i; } } return -1;

}

Note that the length of the main string is m and the length of the pattern string is n. the time complexity of violent matching is O(mn) and the space complexity is O(1);

BM

Violent matching does not use some a priori information of the main string Assuming that the first character of the pattern string is' a ', we can remember the position of' a 'in the main string, and then match the position of' a 'in the main string with the pattern string, which can reduce some comparison times (in fact, the worst time complexity is not improved.)

The following BM uses some prior information in the main string and pattern string to improve the spatial complexity, but reduce the time complexity. Unlike violent matching, BM algorithm traverses from right to left Why do I need to traverse from right to left? Let's first look at the two rules of BM algorithm

Bad character principle

For the pattern string, match from right to left. If it is an error match, remember the character a of the main string, find the next character matching the character a of the main string from right to left in the pattern string, and then move the pattern string to this position If not found, move the entire pattern string after this character

As follows:

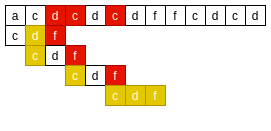
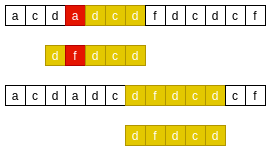
1. From right to left, if the main string'd 'does not match the mode string' f ', find the next character matching the main string'd' in the mode string from right to left;
2. Align the next character of the pattern string with the character matching the main string'd ';

[external chain picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-qydk0hsy-1629955124212)( https://z3.ax1x.com/2021/04/06/c1Rym8.png )]

BM bad character principle I

1. From right to left, if the main string 'c' does not match the mode string 'f', find the next character matching the main string 'c' from right to left in the mode string;
2. Align the next character of the pattern string with the character matching the main string 'c';

[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-p3eg7k8j-1629955124214)( https://z3.ax1x.com/2021/04/06/c1R560.png )]

BM bad character principle 2

1. Pattern string matching succeeded

[external chain picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-yzkf2xfu-1629955124216)( https://z3.ax1x.com/2021/04/06/c1RH7F.png )]

BM bad character principle 3

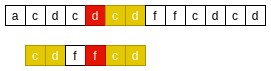
For the example of matching in BF, using the bad character principle of BM can reduce the number of matches:

1. From right to left, if the main string'd 'does not match the mode string' f ', find the next character matching the main string'd' in the mode string from right to left;
2. Align the next character of the pattern string with the character matching the main string'd ';
3. From right to left, if the main string 'c' does not match the mode string 'f', find the next character matching the main string 'c' from right to left in the mode string;
4. Align the next character of the pattern string with the character matching the main string 'c';
5. From right to left, if the main string 'c' does not match the mode string 'f', find the next character matching the main string 'c' from right to left in the mode string;
6. Align the next character of the pattern string with the character matching the main string 'c';
7. Pattern string matching succeeded

Comparison of BM and BF

Take another special example:

First, according to the bad character principle, from right to left, if the main string'd 'does not match the mode string' c ', find the next character matching the main string'd' in the mode string from right to left. If not, move the mode string to the back of the main string'd ':

[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-4iw0p7d2-1629955124220)( https://z3.ax1x.com/2021/04/06/c1f3VO.png )]

BM bad character principle 3

Next, the main string 'c' matches the pattern string 'c', but the main string'd 'does not match the pattern string' f ', and the next'd' cannot be found in the substring. At this time, we can still move the pattern string according to the bad character principle, but the information that the main string 'c' matches the pattern string 'c' is useless

Is there any way to use the matched substring information? This is the good prefix principle of BM algorithm

Good prefix principle

Let's look at an example to match the following string:

[external chain picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-khb4j0ny-1629955124221)( https://z3.ax1x.com/2021/04/06/c14wE8.png )]

BM good prefix principle I

First, we can match according to the bad suffix principle. After moving the pattern string, we find that there is already a sub string that matches well. At this time, we can trigger the good prefix principle

As follows, the "cd" of the mode string matches the "cd" of the main string, but the main string'd 'does not match the mode string' f '. At this time, find the next "cd" substring in the mode string from right to left. If found, align the next "cd" substring of the mode string with the "cd" substring of the main string

BM good prefix principle II

Now the match is successful

BM good prefix principle 3

What if the next substring matching "cd" is not found in the pattern string? There are two situations to consider at this time:

1. If the mode string header has a substring of a substring, align the maximum substring of the mode string header substring with the substring of the main string;
2. If there is no substring in the pattern string header, move the pattern string to the back of the substring of the main string

Examples are as follows:

1. If the main string'd 'matches the mode string'd', and the main string 'a' does not match the mode string 'c', find the next substring matching "d" in the mode string and align it with the main string:

   [external chain picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-i6kgfepn-1629955124226)( https://z3.ax1x.com/2021/04/06/c15PKI.png )]

   BM good prefix Principle 4

2. The main string 'dcd' matches the mode string 'dcd', and the main string 'a' does not match the mode string 'f'. The next substring matching "dcd" is not found in the mode string, but the "d" of the mode string header is a substring of the substring "dcd", so align "d":

   

   BM good prefix Principle 5

Question: why align with the end "d" instead of the first "d"?

If it is aligned with the first "d", there must be no second "dcd" substring in the pattern string, so it must not match. Just align it with the end "d"

Reflections on the two principles of BM

• Question 1: why right to left matching?

For bad characters or good prefixes, matching from right to left allows us to move the least distance to prevent missing some matches

• Question 2: why does the bad character principle work?

If the substring of the bad character may match the pattern string, there must be a character matching the bad character in the pattern string So the bad character principle just tries the following possibilities

• Question 3: why does the good prefix principle work?

In the same problem 2, if a good prefix is a possible match, there must be another matching suffix or suffix substring in the pattern string

• Question 4: when are bad characters and good prefixes?

According to the explanation of question 1, the two principles are to move the distance as small as possible under the condition of ensuring a certain matching string. Using a certain principle alone and some boundary processing conditions may also complete the matching process. In order to speed up the algorithm, the result with the longest moving distance among bad characters and good prefixes can be used

• Question 5: how to use the bad character principle alone?

If bad characters are encountered and other characters matching the bad characters are found, the bad character principle can be used normally What if you don't find it? Whether there is a good prefix or not, move the pattern string after the bad character and try to match again

• Question 6: how to use the prefix principle alone?

In the same bad character principle, if there is a match, it will match normally. If there is no match, move the matching string to the back of the good suffix

BM code implementation

Code implementation of bad characters

The simple implementation of the bad character principle is relatively simple. Each time a bad character is encountered, find the next character matching the bad character from right to left But this operation is very inefficient Because we are looking for a character in the pattern string, we can consider using a map to record the last position of the character in the pattern string:

1 2 3 4 5 6 7 8 9

void badChar(unordered_map<char, int> &badmps, const string &pstr) { int size = pstr.size(); for (int i = 0; i < size; i++) { //badmps represents the rightmost position of the character of the pattern string badmps[pstr[i]] = i; } }

Another function is provided to calculate the moving distance:

1 2 3 4 5 6 7

int badMove(unordered_map<char, int> &badmps, const char &badc, const int &pos) { //Although it may be negative, we are not very careful //1. Negative numbers can be replaced by shifting one bit to the right //2. Increase the complexity. Instead of matching the rightmost matching of the pattern string, it matches the rightmost matching of the right substring of the pattern string bounded by bad characters return badmps.find(badc) != badmps.end() ? pos - badmps[badc] : -1; }

Good prefix code implementation

Good prefix principle, we need to implement two places:

1. The rightmost substring that exactly matches the good prefix;
2. If there is no exactly matched substring, the partially matched substring of the header is found

Referring to the general solution, the following code can be realized:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

void goodMatch(vector<int> &sufix, vector<bool> &prefix, const string &pstr) { int size = pstr.size(); sufix.reserve(size); prefix.reserve(size); for (int i = 0; i < size; ++i) { //sufix[i] indicates the position of the substring with length I. note that the substring with length I is unique //-1, this substring does not exist sufix[i] = -1; //prefix[i] indicates whether the substring is in the header prefix[i] = false; } int pstr_max_index = size - 1; //There is no need to traverse the entire pattern string, because when the length is full, there must be no other substrings for (int i = 0; i &lt; pstr_max_index; i++) { //Is the initial position of traversal, from right to left int j = i; //k is used to record the length of the substring int k = 0; //So we always get the right most sufix while ((j &gt;= 0) &amp;&amp; (pstr[j] == pstr[pstr_max_index - k])) { sufix[++k] = j--; } if (j &lt; 0) { prefix[k] = true; } }

}

Why?

Because the substring to be matched is known, that is, the substring of the pattern string, obtaining the position of these constant substrings during preprocessing can reduce some calculation and time complexity during processing

After preprocessing, you also need a function to calculate the offset:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

int goodMove(const vector<int> &sufix, const vector<bool> &prefix, const int &mlen, const int &pos) { if (mlen < 1) return -1; int move_len = 0; int size = sufix.size(); move_len = sufix[mlen]; if (move_len < 0) { for (int i = mlen - 1; i > 0; i--) { if (prefix[i] == true) { move_len = sufix[i]; break; } } } return pos - move_len;

}

BM complete code

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

int strStr(string haystack, string needle) { //There are few boundary conditions. Deal with them first if (needle.empty()) return 0; int sh = haystack.size(); int sn = needle.size(); if (sh < sn) return -1; //Pretreatment unordered_map<char, int> badmps; badChar(badmps, needle); vector<int> sufix; vector<bool> prefix; goodMatch(sufix, prefix, needle); int i = 0; while (i <= (sh - sn)) { int j = sn - 1; int mlen = 0; char bad_char = 0; while (j >= 0) { if (haystack[i + j] != needle[j]) { bad_char = haystack[i + j]; break; } mlen++; j--; } if (mlen >= sn) { return i; } //Get the position of the mismatched character int pos = sn - mlen - 1; int bad_step = badMove(badmps, bad_char, pos); int good_step = goodMove(sufix, prefix, mlen, pos); int step = max(bad_step, good_step); if (step < 0) step = sn; i += (step > 0 ? step : 1); } return -1;

}