Article catalog

• Suffix tree
• Suffix Array
• • concept
  • sa[]
  • rk[]
  • height[]
• Examples
• • HDU-1403 longest common substring
  • Number of different substrings of Luogu P2408
  • HDU-5769Substring

Suffix tree

It is recommended to understand it first Dictionary tree.

First, understand the concept of suffix. Suffix is a substring from a certain position to the end. For example, the string s=aabab, whose five suffixes are aabab, abab, bab, ab, b.

Suffix tree is a tree that uses dictionary tree method to build all suffix substrings, as shown in the figure:

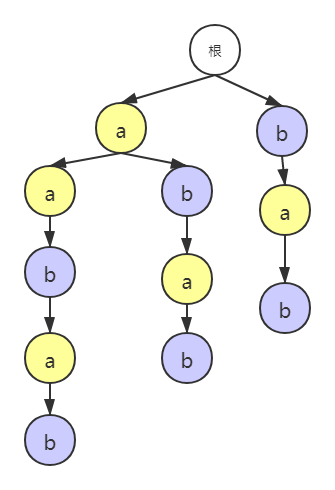
If the root node is empty, you can also use a '$' symbol after the leaf node to identify the end, and all substrings can be reached from the root node.

Template:

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100005;
int trie[maxn][26];
int pos = 1, n;
char s[maxn], t[maxn];
void insert(int idx) { //Build suffix tree
    int p = 0; 
    for (int i = idx; i < n; i++) {
        int u = s[i] - 'a';
        if (trie[p][u] == 0)
            trie[p][u] = pos++;
        p = trie[p][u];
    }
}
bool find() {  //Query whether it is a substring
    int p = 0;
    for (int i = 0; s[i]; i++) {
        int u = s[i] - 'a';
        if (trie[p][u] == 0)
            return false;
        p = trie[p][u];
    }
    return true;
}
int main() {
    scanf("%s%s", s,t);
    n = strlen(s);
    for (int i = 0; i < n; i++) {//Enumeration starting point
        insert(i);
    }
    printf("%s Substring", find() ? "yes" : "no");
    return 0;
}

However, it is not difficult to find that the time and space cost of building trees are very high. Suffix array and suffix automata can be regarded as optimizing the time and space of suffix tree, avoiding tree building and improving the reuse rate of tree nodes through mapping relationship.

Suffix Array

concept

It is not convenient to construct and program suffix tree directly, and suffix array is a simpler alternative.

Suffix array is the suffix subscript corresponding to dictionary order, that is, sa (suffix array abbreviation) array. For example, s[1]=3 indicates that the substring of dictionary order 1 is the suffix substring starting at the third position in the original string, i.e. ab.

Some string problems can be easily solved through the suffix array. For example, to find the substring t in the parent string s, you only need to do a binary search on sa []. The time complexity is O(mlogn), m substring length n parent string length, such as finding ba:

#include<bits/stdc++.h>
using namespace std;
string s, t;
int sa[] = { 0,3,1,4,2 }; //Let sa [] be found
int find() {  //t position in s
    int l = 0, r = s.size();
    while (r > l + 1) { //Dichotomy in dictionary Preface
        int mid = (l + r) / 2;
        if (s.compare(sa[mid], t.length(), t) < 0)
            l = mid;  //-1 unequal movement of the left pointer
        else r = mid; //0 moves the right pointer equally
    }
    if (s.compare(sa[r], t.length(), t) == 0)
        return sa[r];  //Return to original position
    if (s.compare(sa[l], t.length(), t) == 0)
        return sa[l];
    return -1; //Can't find
}
int main() {
    s = "aabab";
    t = "ba";
    cout << find();
    return 0;
}

sa[]

The problem now is how to efficiently find the suffix array sa [], that is, sort the suffix substrings?

If you directly use fast sorting, there is O(n) comparison between each two strings, so the total complexity is O(n^2logn), which is obviously not friendly. The answer is to use the multiplication method.

1. Replace letters with numbers, such as a=0, b=1.
2. The combination of two consecutive numbers, for example, 00 represents aa, 01 represents ab, and the last 1 has no follow-up. Add 0 to the tail to form 10, which does not affect the comparison of characters.
3. Four consecutive numbers are combined. For example, 0010 represents aaba. Similarly, 01 and 10 are obtained. There is no follow-up, and 0 is supplemented.
4. Get five completely different numbers. You can distinguish between sizes. Sort them to get rk array = {0,2,4,1,3}.
5. Finally, the suffix array sa[]={0,3,1,4,2} is obtained by ranking.

Each of the above steps is incremented by twice, with a total of log(n) steps. However, when the string is very long, the generated combined number is likely to overflow. At this time, a compression is required for each step, as long as the relative order remains the same, as follows:

rk[]

That is to say, the suffix array sa [] needs to be found through a ranking rk []. The two are one-to-one correspondence. They are inverse operations and can be deduced from each other, that is, sa[rk[i]]=i, rk[sa[i]]=i.

• sa [] suffix array, short for suffix array, records the position and who ranks i in the dictionary order.
• rk [] ranking array, short for rank array, records the ranking, which is the ranking of the i-th suffix substring.

After getting the multiplied relative size number, we can directly use fast sort() to get rk []. Each time we fast sort O(nlogn), we need to fast log(n) times, and the total complexity is O(n(logn)^2). Template:

#include<bits/stdc++.h>
using namespace std;
const int maxn = 200005;
char s[maxn];
int sa[maxn], rk[maxn], tmp[maxn + 1];
int n, k;
bool cmp_sa(int i, int j) { //Direct comparison eliminates the combination process
    if (rk[i] != rk[j]) //High order of comparison combination number
        return rk[i] < rk[j];
    else { //Compare the low order of combination number
        int ri = i + k <= n ? rk[i + k] : -1;
        int rj = j + k <= n ? rk[j + k] : -1;
        return ri < rj;
    }
}
void calc_sa() { //Calculate sa [] (quick sort)
    for (int i = 0; i <= n; i++) {
        rk[i] = s[i]; //Record the original value
        sa[i] = i; //Record the current sorting result
    }
    for (k = 1; k <= n; k *= 2) { //Double each time
        sort(sa, sa + n, cmp_sa);
        //Because rk [] has the same number, it needs the previous round of RK [] to compare (i.e. in cmp_sa)
        //Therefore, it cannot be directly assigned to rk [] and requires a tmp [] turnover
        tmp[sa[0]] = 0; 
        for (int i = 0; i < n; i++) //sa [] backward combination number is recorded in tmp []
            tmp[sa[i + 1]] = tmp[sa[i]] + (cmp_sa(sa[i], sa[i + 1]) ? 1 : 0);
        for (int i = 0; i < n; i++)
            rk[i] = tmp[i];
    }
}
int main() {
    memcpy(s, "aabab", 6);
    n = strlen(s);
    calc_sa();
    for (int i = 0; i < n; i++)
        cout << sa[i] << " ";
    // 0 3 1 4 2
    return 0;
}

In addition to using Quick sort directly, there is also a faster sorting method - cardinal sorting. The total complexity is only O(nlogn), which is crazy when there is a problem card.

Cardinality sorting is to compare the low bit first and then the high bit. Using the idea of hash, the same number of this bit is directly placed in the corresponding grid. If {82,43,67,52,91,40} is sorted, first {40,91,82,52,43,67} is sorted by one bit, then {40,43,52,67,82,91} is sorted by ten bits, and so on.

Template:

#include<bits/stdc++.h>
using namespace std;
const int maxn = 200005;
char s[maxn];
int sa[maxn], rk[maxn];
int cnt[maxn], t1[maxn], t2[maxn];
int n, k;
void calc_sa() { //Calculate sa[] (cardinality sort)
    int m = 127; //ASCLL scope
    int i, * x = t1, * y = t2;
    for (i = 0; i < m; i++)cnt[i] = 0;
    for (i = 0; i < n; i++)cnt[x[i] = s[i]]++;
    for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
    for (i = n - 1; i >= 0; i--)sa[--cnt[x[i]]] = i;
    for (k = 1; k <= n; k *= 2) {
        int p = 0; //The sorting result of length k is used to sort length 2k
        for (i = n - k; i < n; i++)y[p++] = i;
        for (i = 0; i < n; i++)
            if (sa[i] >= k)y[p++] = sa[i] - k;
        for (i = 0; i < m; i++)cnt[i] = 0;
        for (i = 0; i < n; i++)cnt[x[y[i]]]++;
        for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
        for (i = n - 1; i >= 0; i--)sa[--cnt[x[y[i]]]] = y[i];
        swap(x, y);
        p = 1;
        x[sa[0]] = 0;
        for (i = 1; i < n; i++)
            x[sa[i]] = y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + k] == y[sa[i] + k] ? p - 1 : p++;
        if (p >= n)break;
        m = p;
    }
}
int main() {
    memcpy(s, "aabab", 6);
    n = strlen(s);
    calc_sa();
    for (int i = 0; i < n; i++)
        cout << sa[i] << " ";
    // 0 3 1 4 2
    return 0;
}

height[]

height [] is an auxiliary array related to the Longest Common Prefix (LCP).

Define height[i] as the longest common prefix length of sa[i-1] and sa[i]. For example, in the previous aabab, sa[1] represents ab, sa[2] represents abab, then height[2]=2.

Compare the adjacent sa [], with the complexity of O(n^2) by violence. The template with the complexity of O(n) is given below:

void getheight(int n) { //n is the string length
    int k = 0;
    for (int i = 0; i < n; i++)
        rk[sa[i]] = i;
    for (int i = 0; i < n; i++) {
        if (k)k--;
        int j = sa[rk[i] - 1];
        while (i + k < n && j + k < n && s[i + k] == s[j + k])k++;
        height[rk[i]] = k;
    }
}

(insert anti climbing information) CSDN address of blogger: https://wzlodq.blog.csdn.net/

Examples

Many string problems can be solved by using suffix array, such as:

1. Find substring t in string s The code given earlier can be found sa[].
2. Find the longest repeating substring height [] in string s The maximum value in the array is the length of the longest repeating substring
3. Find the longest common substring of string s1 and string s2 Merge string s1 and string s2 into string s3, and insert a '$' in the middle, which is converted to finding the maximum repeated substring. However, it is necessary to judge whether the corresponding sa[i] and sa[i-1] belong to the two strings before and after '$' respectively.
4. Find the largest palindrome substring of string s Manacher (horse drawn cart) algorithm is generally used.

HDU-1403 longest common substring

HDU-1403 Longest Common Substring

Given two strings, you have to tell the length of the Longest Common Substring of them. For example: str1 = banana str2 = cianaic So the Longest Common Substring is "ana", and the length is 3. Input The input contains several test cases. Each test case contains two strings, each string will have at most 100000 characters. All the characters are in lower-case. Process to the end of file. Output For each test case, you have to tell the length of the Longest Common Substring of them. Sample Input banana cianaic Sample Output 3

#include<bits/stdc++.h>
using namespace std;
const int maxn = 200005;
char s[maxn];
int sa[maxn], rk[maxn], height[maxn];
int cnt[maxn], t1[maxn], t2[maxn];
int n, k;
void calc_sa() {
    int m = 127;
    int i, * x = t1, * y = t2;
    for (i = 0; i < m; i++)cnt[i] = 0;
    for (i = 0; i < n; i++)cnt[x[i] = s[i]]++;
    for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
    for (i = n - 1; i >= 0; i--)sa[--cnt[x[i]]] = i;
    for (k = 1; k <= n; k *= 2) {
        int p = 0;
        for (i = n - k; i < n; i++)y[p++] = i;
        for (i = 0; i < n; i++)
            if (sa[i] >= k)y[p++] = sa[i] - k;
        for (i = 0; i < m; i++)cnt[i] = 0;
        for (i = 0; i < n; i++)cnt[x[y[i]]]++;
        for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
        for (i = n - 1; i >= 0; i--)sa[--cnt[x[y[i]]]] = y[i];
        swap(x, y);
        p = 1;
        x[sa[0]] = 0;
        for (i = 1; i < n; i++)
            x[sa[i]] = y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + k] == y[sa[i] + k] ? p - 1 : p++;
        if (p >= n)break;
        m = p;
    }
}
void getheight(int n) {
    int k = 0;
    for (int i = 0; i < n; i++)
        rk[sa[i]] = i;
    for (int i = 0; i < n; i++) {
        if (k)k--;
        int j = sa[rk[i] - 1];
        while (i + k < n && j + k < n && s[i + k] == s[j + k])k++;
        height[rk[i]] = k;
    }
}
int main() {
    while (~scanf("%s", s)) {
        int len1 = strlen(s);
        s[len1] = '$';
        scanf("%s", s + len1 + 1);
        n = strlen(s);
        calc_sa();
        getheight(n);
        int ans = 0;
        for (int i = 1; i < n; i++) {
            if (height[i] > ans) {
                if ((sa[i] < len1 && sa[i - 1] >= len1) || sa[i - 1] < len1 && sa[i] >= len1)
                    ans = height[i];
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

This problem is nearly ten times faster than the radix sorting.

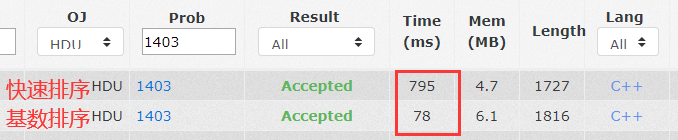
Number of different substrings of Luogu P2408

P2408 number of different substrings

Topic background Because NOI was abused and stupid, konjaku's YJQ was ready to learn the string, so it encountered such a problem: Title Description Give you a string with length N and find the number of different substrings We define that two substrings are different if and only if the length of these two substrings is different or the length is the same and any bit is different. Definition of substring: a string consisting of a continuous section of characters in the original string Input format The first line is an integer N The next line of N characters represents the given string Output format One integer per line represents the number of different substrings Input and output samples Enter #1 5 aabaa Output #1 11 Enter #2 3 aba Output #2 5 Description / tips Please use a 64 bit integer for output (specifically, for C + + and C players, please use long long type, and for pascal players, please use Int64) Because the input file is too large, please use an efficient read method (specifically, c + + and c players do not use cin, pascal players do not need to manage) For 30% data, N ≤ 1000 For 100% data, N ≤ 105

Each suffix sa[i] generates n-sa[i] prefixes, and height[i] of these prefixes are repeated, that is, n-sa[i]-height[i] different substrings are generated.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 200005;
char s[maxn];
int sa[maxn], rk[maxn], height[maxn];
int cnt[maxn], t1[maxn], t2[maxn];
int n, k;
void calc_sa() {
    int m = 127;
    int i, * x = t1, * y = t2;
    for (i = 0; i < m; i++)cnt[i] = 0;
    for (i = 0; i < n; i++)cnt[x[i] = s[i]]++;
    for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
    for (i = n - 1; i >= 0; i--)sa[--cnt[x[i]]] = i;
    for (k = 1; k <= n; k *= 2) {
        int p = 0;
        for (i = n - k; i < n; i++)y[p++] = i;
        for (i = 0; i < n; i++)
            if (sa[i] >= k)y[p++] = sa[i] - k;
        for (i = 0; i < m; i++)cnt[i] = 0;
        for (i = 0; i < n; i++)cnt[x[y[i]]]++;
        for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
        for (i = n - 1; i >= 0; i--)sa[--cnt[x[y[i]]]] = y[i];
        swap(x, y);
        p = 1;
        x[sa[0]] = 0;
        for (i = 1; i < n; i++)
            x[sa[i]] = y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + k] == y[sa[i] + k] ? p - 1 : p++;
        if (p >= n)break;
        m = p;
    }
}
void getheight(int n) {
    int k = 0;
    for (int i = 0; i < n; i++)
        rk[sa[i]] = i;
    for (int i = 0; i < n; i++) {
        if (k)k--;
        int j = sa[rk[i] - 1];
        while (i + k < n && j + k < n && s[i + k] == s[j + k])k++;
        height[rk[i]] = k;
    }
}
int main() {
    scanf("%d%s", &n, s);
    n++;
    calc_sa();
    getheight(n);
    n--;
    ll ans = 0;
    for (int i = 1; i <= n; i++)
        ans += n - sa[i] - height[i];
    printf("%lld", ans);
    return 0;
}

HDU-5769Substring

HDU-5769 Substring

?? is practicing his program skill, and now he is given a string, he has to calculate the total number of its distinct substrings. But ?? thinks that is too easy, he wants to make this problem more interesting. ?? likes a character X very much, so he wants to know the number of distinct substrings which contains at least one X. However, ?? is unable to solve it, please help him. Input The first line of the input gives the number of test cases T;T test cases follow. Each test case is consist of 2 lines: First line is a character X, and second line is a string S. X is a lowercase letter, and S contains lowercase letters('a'-'z') only. T<=30 1<=|S|<=10^5 The sum of |S| in all the test cases is no more than 700,000. Output For each test case, output one line containing "Case #x: y"(without quotes), where x is the test case number(starting from 1) and y is the answer you get for that case. Sample Input 2 a abc b bbb Sample Output Case #1: 3 Case #2: 3 Hint In first case, all distinct substrings containing at least one a: a, ab, abc. In second case, all distinct substrings containing at least one b: b, bb, bbb.

After the suffixes are sorted according to the dictionary order, the prefixes of the two adjacent suffixes must be the same (height array record), so there is no need to think twice. The location of the nearest target character behind each letter in the record must contain at least this letter.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 200005;
char s[maxn];
int sa[maxn], rk[maxn], height[maxn];
int cnt[maxn], t1[maxn], t2[maxn];
int n, k;
void calc_sa() {
    int m = 127;
    int i, * x = t1, * y = t2;
    for (i = 0; i < m; i++)cnt[i] = 0;
    for (i = 0; i < n; i++)cnt[x[i] = s[i]]++;
    for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
    for (i = n - 1; i >= 0; i--)sa[--cnt[x[i]]] = i;
    for (k = 1; k <= n; k *= 2) {
        int p = 0;
        for (i = n - k; i < n; i++)y[p++] = i;
        for (i = 0; i < n; i++)
            if (sa[i] >= k)y[p++] = sa[i] - k;
        for (i = 0; i < m; i++)cnt[i] = 0;
        for (i = 0; i < n; i++)cnt[x[y[i]]]++;
        for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
        for (i = n - 1; i >= 0; i--)sa[--cnt[x[y[i]]]] = y[i];
        swap(x, y);
        p = 1;
        x[sa[0]] = 0;
        for (i = 1; i < n; i++)
            x[sa[i]] = y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + k] == y[sa[i] + k] ? p - 1 : p++;
        if (p >= n)break;
        m = p;
    }
}
void getheight(int n) {
    int k = 0;
    for (int i = 0; i < n; i++)
        rk[sa[i]] = i;
    for (int i = 0; i < n; i++) {
        if (k)k--;
        int j = sa[rk[i] - 1];
        while (i + k < n && j + k < n && s[i + k] == s[j + k])k++;
        height[rk[i]] = k;
    }
}
int main() {
    int t;
    scanf("%d", &t);
    for (int cs = 1; cs <= t; cs++) {
        char x[3];
        scanf("%s%s", x, s);
        n = strlen(s);
        n++;
        calc_sa();
        getheight(n);
        n--;
        int nex[maxn];
        int pos = n;
        for (int i = n - 1; i >= 0; i--) {
            if (s[i] == x[0])pos = i;
            nex[i] = pos;
        }
        ll ans = 0;
        for (int i = 1; i <= n; i++) {
            ans += n - max(nex[sa[i]], sa[i] + height[i]);
        }
        printf("Case #%d: %lld\n", cs, ans);
    }
    return 0;
}