4.0 Content Overview

Concepts that are important to the overall knowledge architecture:

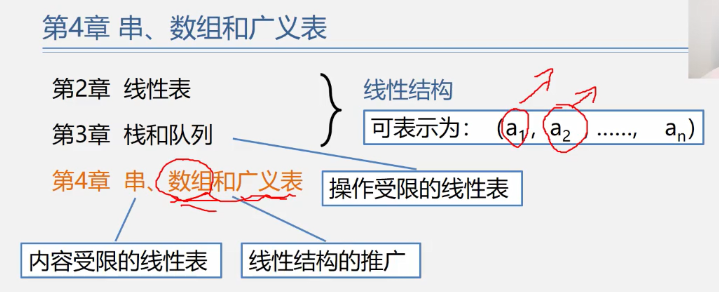
The element of a string can only be a character;
The elements in the array are linear tables;
Elements in a generalized table are also generalized tables.
Strictly speaking, arrays and generalized tables are not linear structures; they are generalizations of linear structures.

4.1 Strings

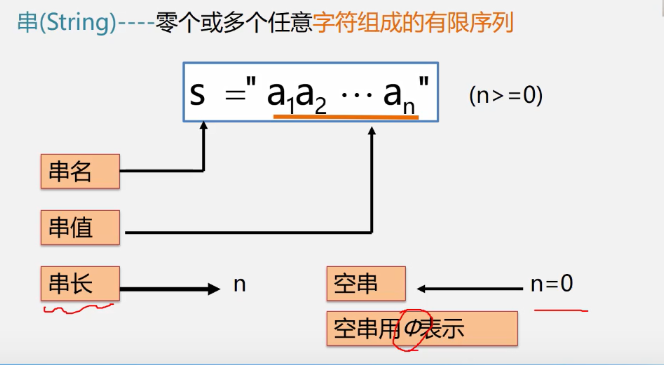
Basic concepts of 4.1.1 string

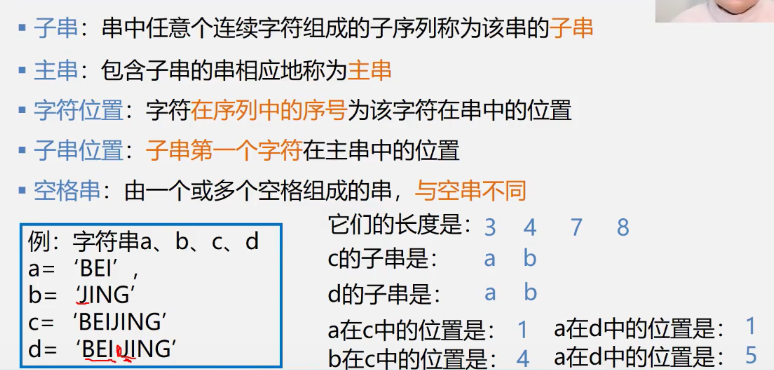
Practical application of 4.1.2 string

Type Definition, Storage Structure and Operations of 4.1.3 Strings

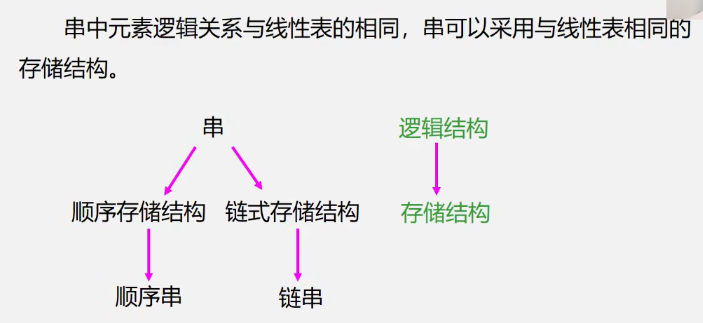
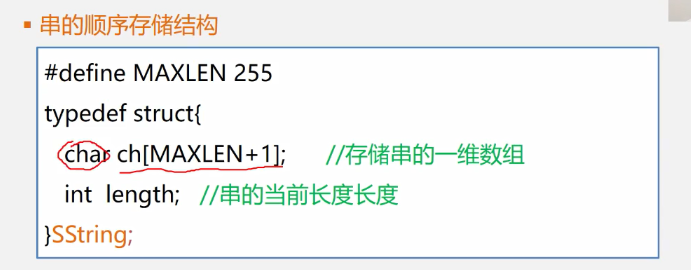
Sequential storage structure of 4.1.3.1 strings

Sequential storage structures are more common because strings are rarely inserted or deleted.

Chain Storage Structure for 4.1.3.2 Series

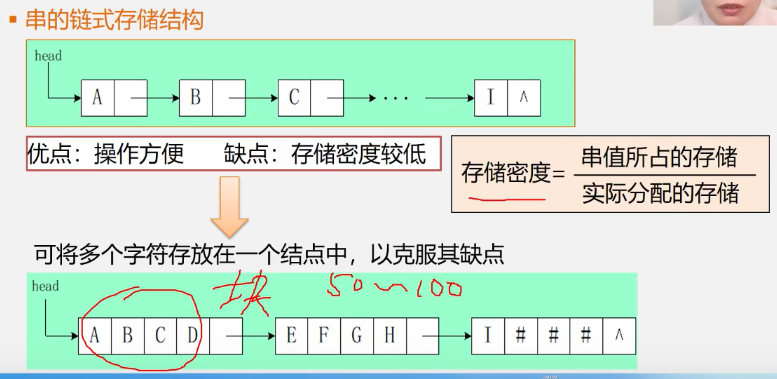
Note: The English word for block is chunk.

Pattern Matching Algorithm for 4.1.3.3 Strings--BF

Since the string algorithm has been learned in advanced languages, the following is mainly about the pattern matching algorithm for strings.

Pattern (Substring) Matching BF Algorithm

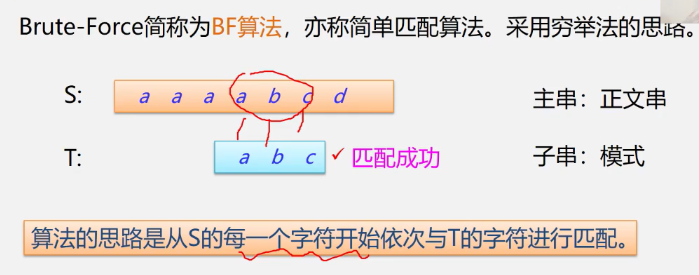
Example

Note: The [0] position of the array in the string structure does not store elements, but begins at the [1] position, so both i and j here start at 1.
Backtrace: After a match fails, i=i-j+2, which can be understood in two steps. First, i-j-1 lets I fall back to where I just started, then + 1, which is the next place to where I just started.


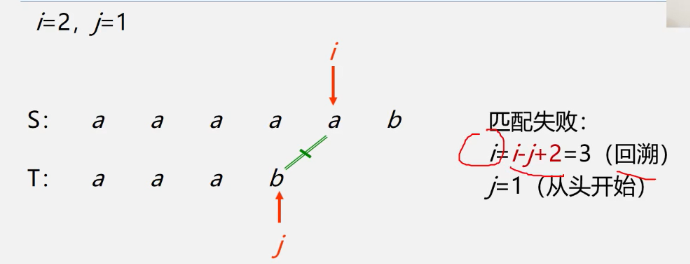
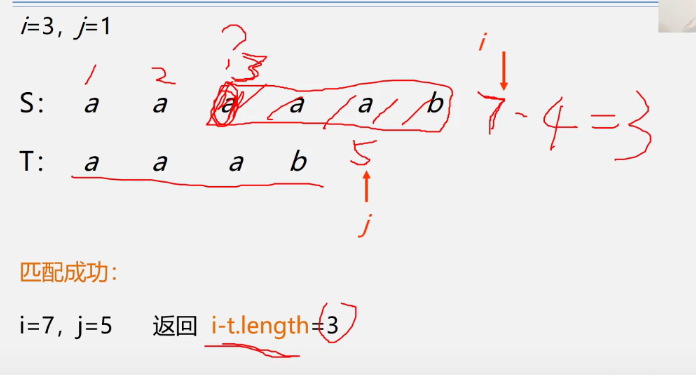
Summary of Algorithmic Thoughts

Algorithmic Description

The [0] position of the array in the string structure does not store elements, but begins at the [1] position, so both i and j here start at 1.

If you need to start looking for pos anywhere

Question if you don't need an = sign in the second line of code if statement from the bottom?

Time Complexity Analysis
At best m and at worst n*m, the analysis is as follows:

Pattern Matching Algorithm for 4.1.3.3 Strings--KMP

Examples of next[j]

KMP algorithm description

Where T represents the pattern string and S represents the main string.

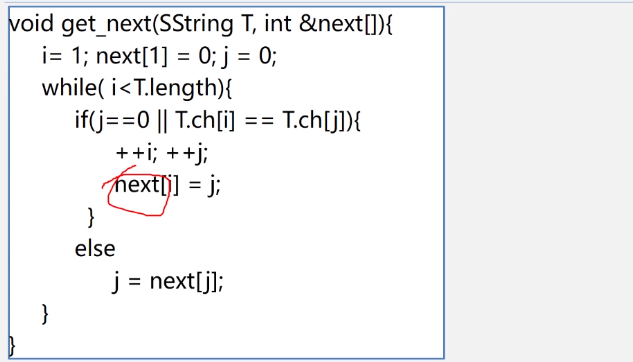
What the teacher said above is that the algorithm is difficult to understand, can be understood, and can be used.

4.2 Array

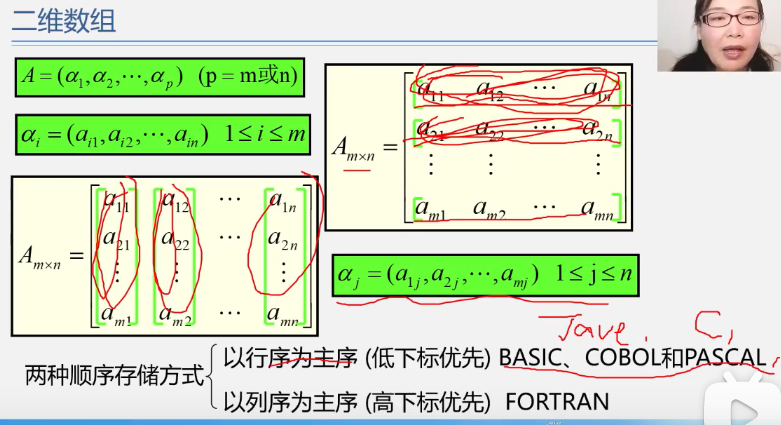
Basic concepts of 4.2.1 arrays

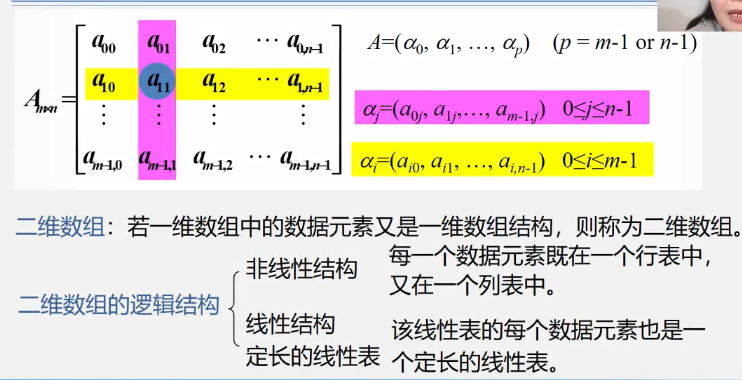
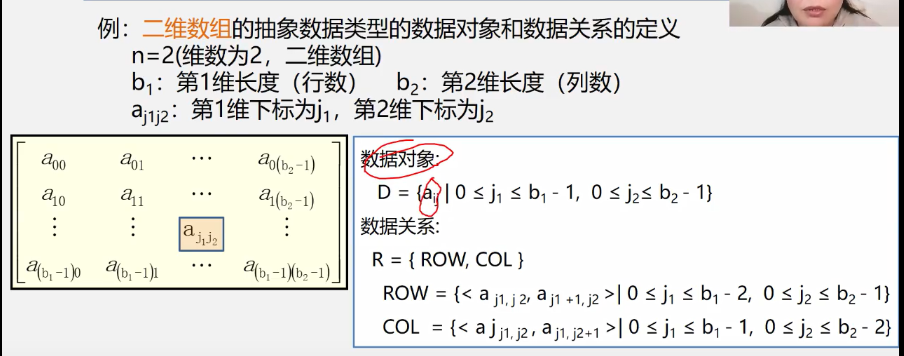
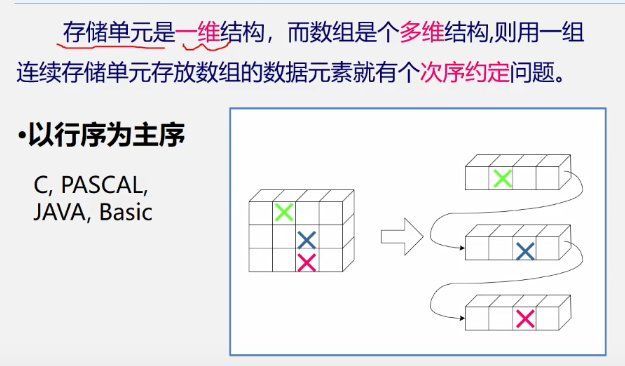
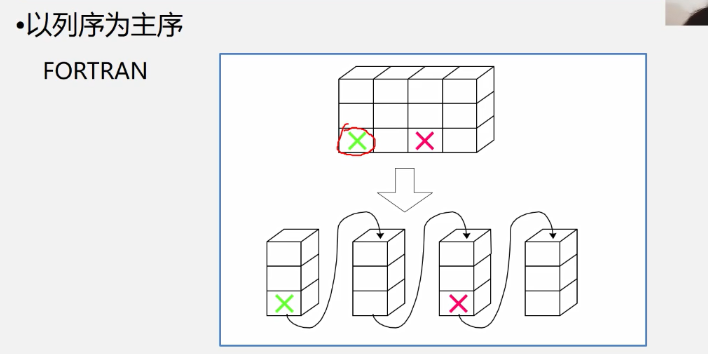
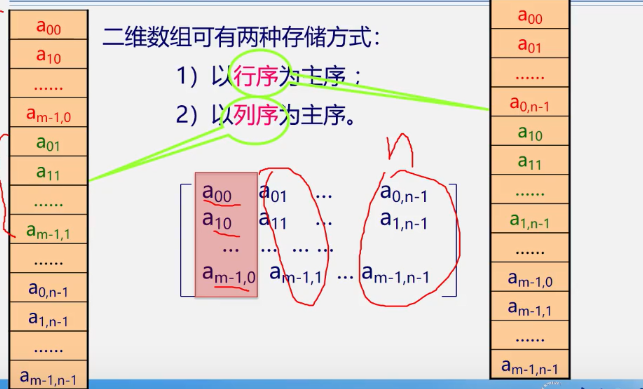
Sequential storage structure for 4.2.2 arrays

Storage and address of one-dimensional arrays

Storage and address of two-dimensional arrays






Example

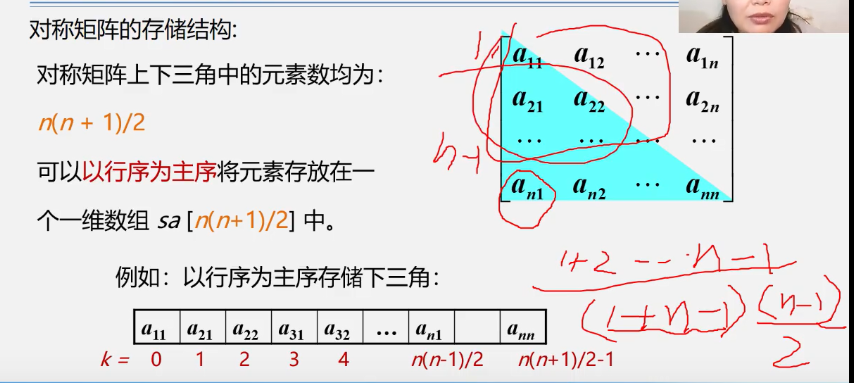
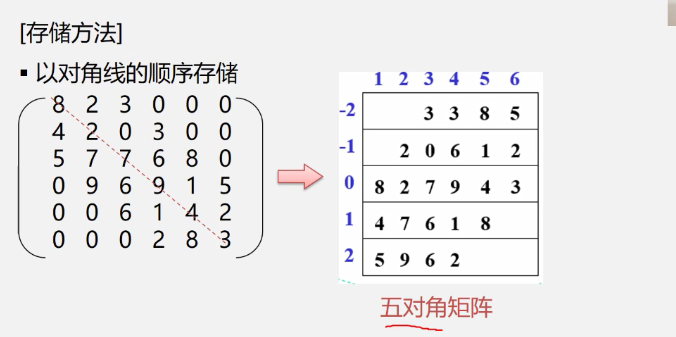
Compressed storage of 4.2.3 Special Matrices

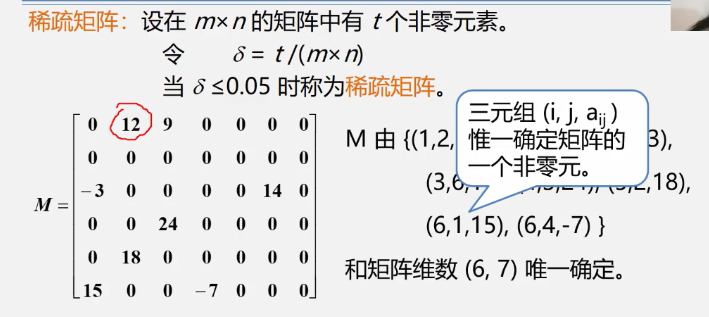
4. Sparse Matrix

Ternary method

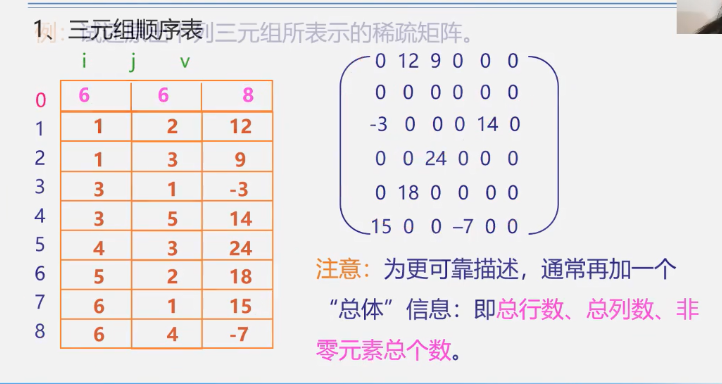
The characteristics of the ternary method:

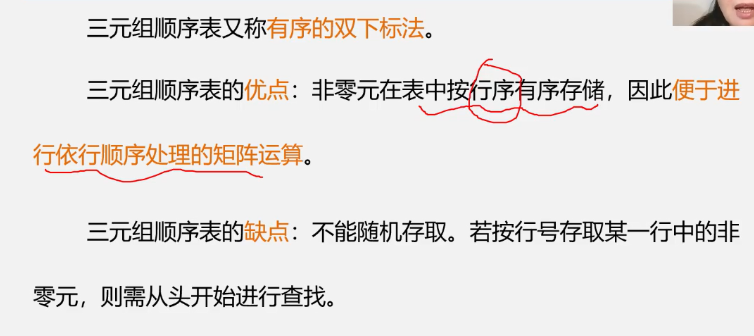
The disadvantage of tuple method is that it cannot be accessed randomly. First, it can only be stored sequentially when it is stored. Without the element before it, you will not know where this element should exist now. Second, when taking a value, you can only search through the information for that value.

Supplement: Random Access, Sequential Access
1. Random access is direct access. It can directly access the element's location through subscripts, regardless of its storage location. Time complexity is always O(1), such as array s. When accessing the Nth data, you can operate directly on the Nth data without accessing the previous (N-1) data.
2. Sequential access, not subscript access. When accessing the Nth data, you must first access the first (N-1) data, such as a linked list.

Orthogonal list

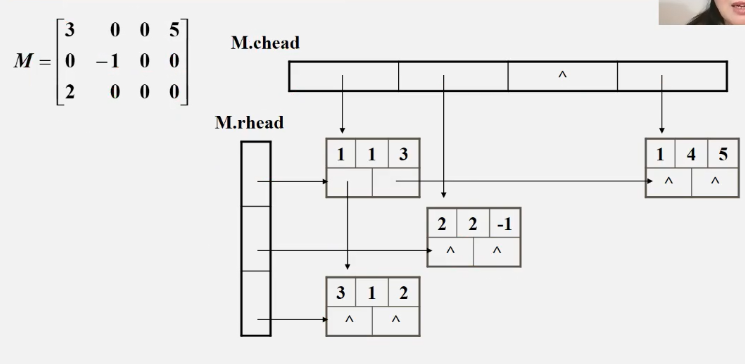
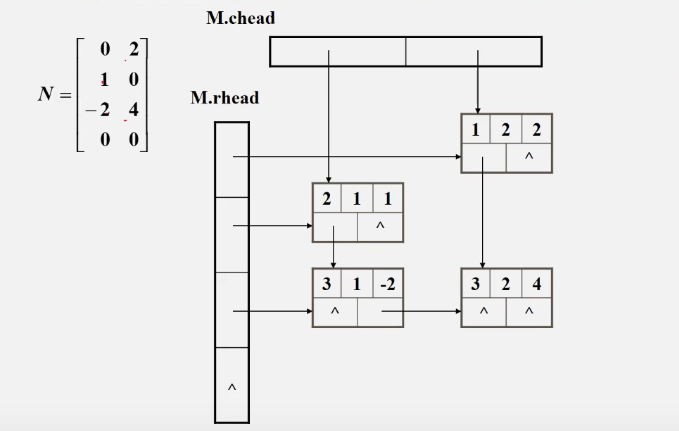
The teacher didn't tell the code, and then she learned it by herself

4.3 Generalized Table

Basic concepts of 4.3.1 generalized tables

Atom: a single element

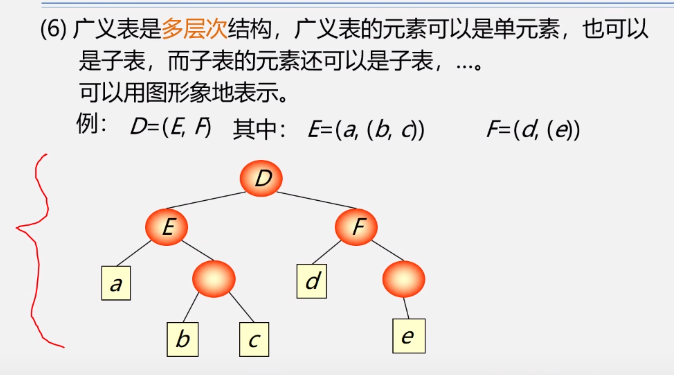
Generalized tables are usually stored in a chain table

4.4 Cases: Viral Infections

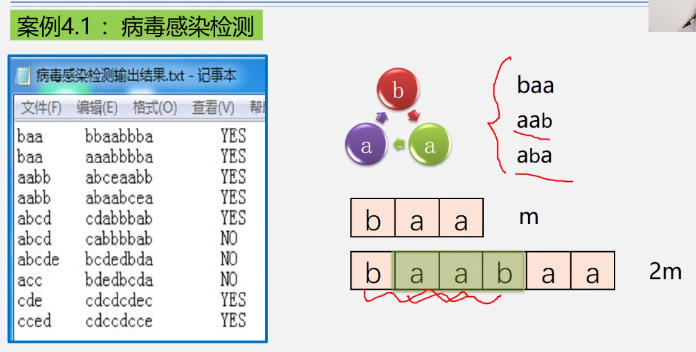
Program implementation:

// Linear Structure_ String_ Pattern (Substring) Matching Problem_ Viral infection. cpp: This file contains the "main" function. Program execution will begin and end here.
//

#include <iostream>
#include<stdlib.h>
using namespace std;


typedef struct {
    char ch[11];
    int length;
}SString;

void CreatS(SString& S) {
    int i = 1;
    while(1) {
        cin >> S.ch[i]; //When entering characters, be sure to separate them with spaces, or they will be strings.
        i++;
        if (cin.get() == '\n') break;
    }
    S.length = i-1;
}

void DoubleS(SString& S) {
    for (int i = 1; i <= S.length; i++) {
        S.ch[i + S.length] = S.ch[i];
    }
    S.length = S.length * 2;
}

SString GetSS(SString& T, int n) {
    SString T_temp;
    for (int i = 1; i <= T.length/2; i++) {
        T_temp.ch[i] = T.ch[n];
        n++;
    }
    T_temp.length = T.length / 2;
    return T_temp;
}

bool index_BF(SString S, SString& T) {
    DoubleS(T);
    for (int n = 0; n < T.length / 2; n++) {
        SString T_temp = GetSS(T, n);
        int i = 1; int j = 1;
        while (i <= S.length && j <= T_temp.length) {
            if (S.ch[i] == T.ch[j]) {
                i++; j++;
            }
            else {
                i = i - j + 2; j = 1;
            }
        }
        if (j >= T_temp.length) {
            return true;
            break;
        }
    }
    return false;
}

void Show(SString S) {
    for (int i = 1; i <= S.length; i++) {
        cout << S.ch[i] << "  ";
    }
    cout << endl;
}

int main()
{
    SString S, T;
    CreatS(S);    
    CreatS(T);
    cout << "Enter results:" << endl;
    Show(S);
    Show(T);
    
    cout <<"Infection:"<< index_BF(S, T);

}