preface

Blocking can solve almost all problems such as interval query and interval update. It is more powerful than segment tree and tree array, but the time complexity will be a little greater. In fact, blocking is an optimized violence. It maintains the whole like a line segment tree and modifies the local violence.

principle

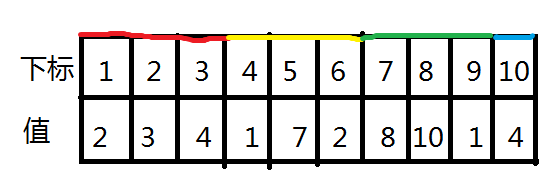
As the name suggests, we divide the sequence with length n into several blocks. Maintain the information in the block.
Again, how big? Typically, the block size is set to n \sqrt n n , use the pos array to store the position of each block.
If there is any left after the final division, the rest will be a separate block.

We use the example of segment tree to introduce PortalluoguP3372

Title Requirements:
1. Interval update:
We can find how many blocks are all in this interval. Because these blocks need to be updated, we can add a lazy flag and update them the next time we need it.
For some blocks in the interval, we can only update these points in the interval violently
2. Interval query:
If the block is included in the interval, you can directly add the value of the processing lazy target and the previous sum.
For blocks with part in the interval, the value can be calculated.

The code is very simple. It's understandable.

#include<bits/stdc++.h>
using namespace std;
#define int long long

const int N=1e5+5;
int n,m,a[N];
int pos[N],sum[N],L[N],R[N],lz[N];
//Block position, sum of blocks, left and right intervals of blocks, lazy flag 

inline void build()
{	
	int t=sqrt(n*1.0);
	int num=n/t;
	if(n%t) num++;//If there is any left, add another block 
	for(int i=1;i<=num;i++)
	{
		L[i]=(i-1)*t+1;//Range of each block 
		R[i]=i*t;
	}
	R[num]=n;//The right interval of the last block is n 
	
	for(int i=1;i<=num;i++)
		for(int j=L[i];j<=R[i];j++)
		{
			pos[j]=i;//Which block does the point belong to 
			sum[i]+=a[j];//Statistics and 
		}
}

inline void update(int l,int r,int k)
{
	int x=pos[l],y=pos[r];
	if(x==y)//The block contains this interval, violence 
	{
		for(int i=l;i<=r;i++)
			a[i]+=k;
		sum[x]+=k*(r-l+1);
	}
	else
	{
		for(int i=x+1;i<=y-1;i++)//All in the interval, lazy mark 
			lz[i]+=k;
		for(int i=l;i<=R[x];i++)//Partly in the interval, violence 
			a[i]+=k;
		sum[x]+=k*(R[x]-l+1);
		for(int i=L[y];i<=r;i++)
			a[i]+=k;
		sum[y]+=k*(r-L[y]+1);
	}
}

inline int query(int l,int r)
{
	int x=pos[l],y=pos[r];//Get the position of the block 
	int ans=0;
	if(x==y)//The block contains this interval, violence 
	{
		for(int i=l;i<=r;i++)
			ans+=a[i];
		ans+=lz[x]*(r-l+1);
	}
	else
	{
		for(int i=x+1;i<=y-1;i++)//Processing lazy Tags 
			ans+=sum[i]+lz[i]*(R[i]-L[i]+1);
		for(int i=l;i<=R[x];i++)//violence 
			ans+=a[i];
		ans+=lz[x]*(R[x]-l+1);
		for(int i=L[y];i<=r;i++)
			ans+=a[i];
		ans+=lz[y]*(r-L[y]+1);
	}
	return ans;
}

signed main()
{
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
	build();//Pretreatment 
	int cas,x,y,k;
	for(int i=1;i<=m;i++)
	{
		scanf("%lld",&cas);
		if(cas==1)
		{
			scanf("%lld%lld%lld",&x,&y,&k);
			update(x,y,k);
		}
		else
		{
			scanf("%lld%lld",&x,&y);
			cout<<query(x,y)<<endl;
		}
	}
	return 0;
}

Another block question PortalHDU4417

The problem requires us to find the number of numbers less than or equal to h in the interval.
First, divide into blocks.
We can't sort the blocks because it will change the position, but we can copy a copy and sort the new array tmp for each block.
For blocks included in the interval, just find the critical point in tmp, and the points below it must be less than or equal to H. you can use upper_bound finds the first number greater than h, then the number below it must be less than or equal to H.
For blocks partially in the interval, we can only enumerate whether these numbers are less than or equal to h, because sorting is to sort the whole, and parts cannot be processed.
Code implementation:

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
int L[N],R[N],pos[N],tmp[N],a[N];
int n,m,t;

inline void build()
{
	int t=sqrt(n*1.0);
	int num=n/t;
	if(n%t) num++;
	for(int i=1;i<=num;i++)
		L[i]=(i-1)*t+1,R[i]=i*t;
	R[num]=n;
	for(int i=1;i<=num;i++)
	{
		for(int j=L[i];j<=R[i];j++)
			pos[j]=i;
		sort(tmp+L[i],tmp+R[i]+1);
	}
}

inline int query(int l,int r,int h)
{
	int ans=0;
	if(pos[l]==pos[r])
	{
		for(int i=l;i<=r;i++)
			if(a[i]<=h) ans++;
	}
	else
	{
		for(int i=l;i<=R[pos[l]];i++)
			if(a[i]<=h) ans++;
		for(int i=L[pos[r]];i<=r;i++)
			if(a[i]<=h) ans++;
		for(int i=pos[l]+1;i<=pos[r]-1;i++)
			ans+=upper_bound(tmp+L[i],tmp+R[i]+1,h)-tmp-L[i];
	}
	return ans;
}

int main()
{
	scanf("%d",&t);
	for(int o=t;o<=t;o++)
	{
		printf("Case %d:\n",o);
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++) scanf("%d",&a[i]),tmp[i]=a[i];
		build();
		int x,y,h;
		for(int i=1;i<=m;i++)
		{
			scanf("%d%d%d",&x,&y,&h);
			cout<<query(x+1,y+1,h)<<endl;
		}
	}
	return 0;
}