I think it's best to solve the subset and problem before using backtracking to solve the 01 knapsack problem.

Problem Description: Yes n n A set of n different positive integers W ={ w 1 , w 2 , w 3 , . . . , w n w_1,w_2,w_3,...,w_n w1​,w2​,w3​,..., wn} and a positive integer Z, it is required to find all subsets in W whose sum is Z.

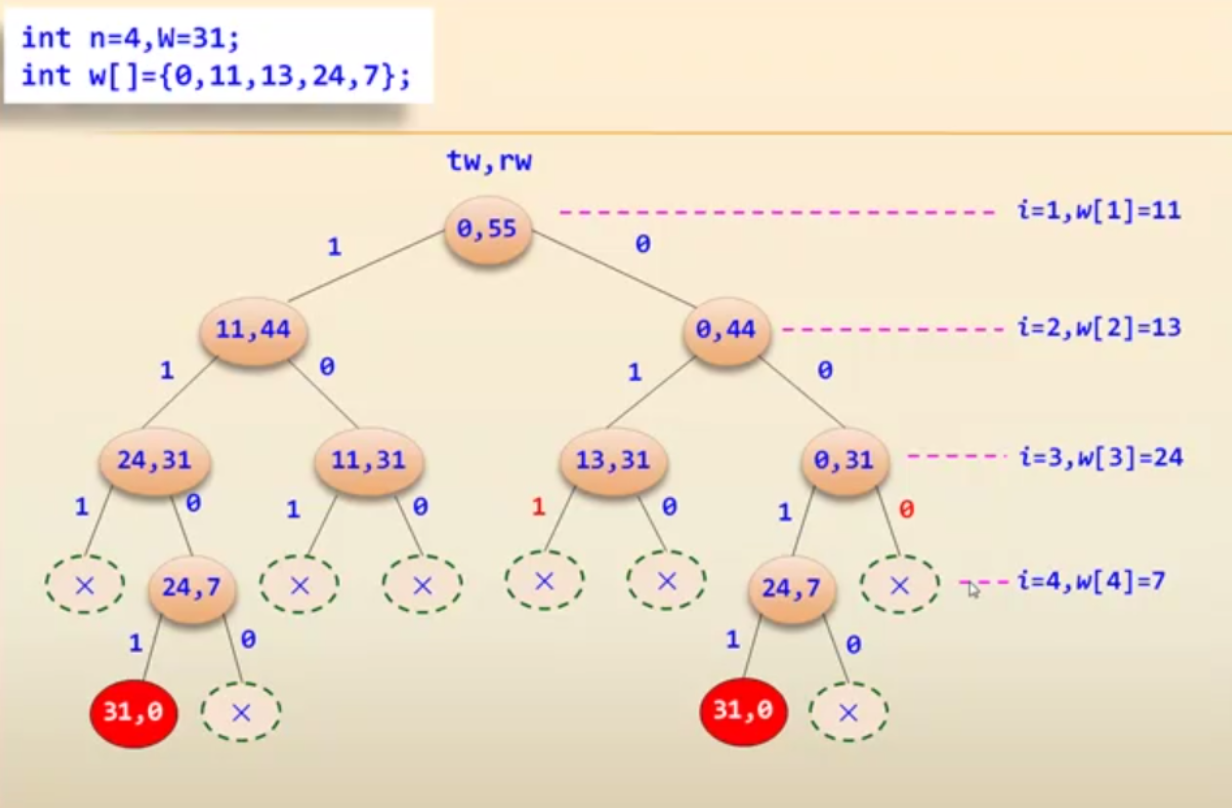
For example, when w = {11, 13, 24, 7}, Z = 31, the subsets meeting the requirements are {11, 13, 7} and {24, 7}

The solution of this problem is actually the first order traversal + pruning of the tree.

For all integers in the set, there are only two possibilities: select or deselect. The first integer is represented by the first layer of the tree, the second integer is represented by the second layer,... Until the nth layer, the following spatial tree of solutions can be obtained.

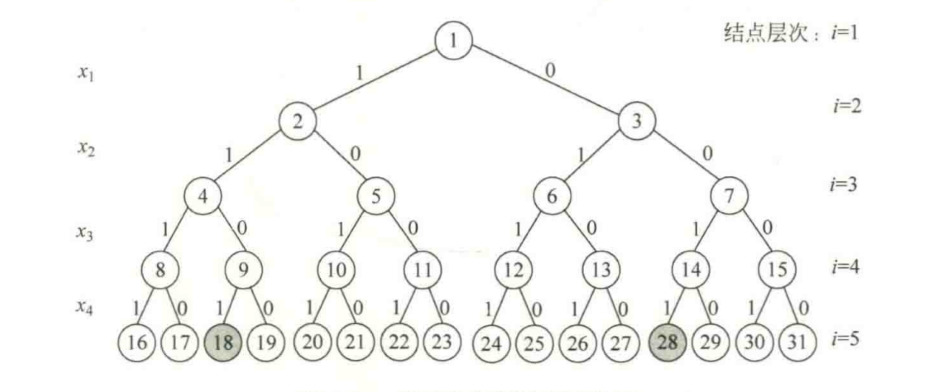
For each node in the spatial tree, extending to the left means that this integer is selected and the tag is set to 1; Extending to the right means that this integer is not selected and the flag is set to 0, so that each leaf node at the bottom represents a combination.

The tree traversal process uses a variable to save the sum of the selected integers, so that each leaf node traversed can judge whether the node on this path is a group of solutions according to the value of the variable.

Obviously, the above results can be obtained, but the spatial tree grows exponentially with the increase of set length. But not every path needs to go to the leaf node to determine whether it is a solution.

If two attributes tw and rw are added to each node, tw represents the sum of the previously selected integers and rw represents the sum of the remaining integers, then:

Constraint function: tw+ w i w_i wi ≤ Z, the function is to select a solution that meets the conditions.
Limit function: tw + rw- w i w_i wi > = Z, or TW + RW > Z, is used to cut off nodes where there is no solution.
Constraint function and bound function are collectively referred to as pruning function. It can be seen that pruning function is actually limiting the space of feasible solution.

After the space of RW + TW has been pruned- w i w_i wi​ >= Z ):

java code

public class SubSetSum {
	public static void search(int[] W, int Z) {
		int n = W.length - 1;
		int[] track = new int[W.length];
		int tw = 0; 								// tw represents the sum of the previously selected integers when considering the ith integer
		int rw = 0; 								// rw represents the sum of the ith and all subsequent integers when the ith integer is considered, and the initial value is the sum of set elements
		for (int i = 1; i < W.length; i++)
			rw += W[i];
		dfs(W, Z, n, tw, rw, track, 1);
	}

	private static void dfs(int[] W, int Z, int n, int tw, int rw, int[] track, int i) {
		// When reaching a leaf node, determine whether it is a solution according to the value of tw in the node
		if (i > n) {	
			if (tw == Z)
				print(track, W);		
		} else { 													// Not all integers found			
			// Prune the left child node and select the integer W[i] that meets the conditions
			if (tw + W[i] <= Z) {
				track[i] = 1; 										// Indicates that the ith integer is selected
				dfs(W, Z, n, tw + W[i], rw - W[i], track, i + 1); 	// Determine the next integer
			}

			// With child nodes, prune out nodes that cannot have solutions
			if (tw + rw - W[i] >= Z) {
				track[i] = 0; 										// Do not select the ith integer
				dfs(W, Z, n, tw, rw - W[i], track, i + 1); 			// Determine the next integer
			}		
		}	
	}

	private static void print(int[] track, int[] W) {
		for (int i = 1; i < track.length; i++) {
			if (track[i] == 1) {
				System.out.print(W[i] + " ");
			}
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int[] set = { 0, 11, 24, 13, 7 }; 							// The subscript 0 position of the array is not used
		search(set, 31);
	}
}

The time complexity is uncertain due to pruning. Because the order of integers passed into the array is different, the state after pruning is also different, and the number of nodes traversed is also different. But because n n The total number of points in the solution space tree of n integers is 2 n + 1 − 1 2^{n+1}-1 2n+1 − 1, so the corresponding worst time complexity O ( 2 n ) Ο(2^n) O(2n).

If there is a solution, it must traverse the underlying leaf node, and the function stack is pressed in the recursive process, which reduces the space complexity O ( l o g 2 n ) Ο(log_ 2n) O(log2​n).

At the same time, it should be noted that:

1. The solution process does not really build this spatial tree.
2. The larger the integer passed into the array, the more obvious the pruning effect.