Binary search algorithm

You can use loops or recursion

Divide and conquer algorithm

Divide a complex problem into two or more identical or similar subproblems, and then divide the subproblem into smaller subproblems... Until the last subproblem can be simply solved directly, and the solution of the original problem is the combination of the solutions of the subproblems.

Divide and conquer algorithm can solve some classical problems
Binary search
Large integer multiplication
Chessboard coverage
Merge sort
Quick sort
Linear time selection
Closest point pair problem
Round robin schedule
Hanoi

Divide and conquer has three steps on each layer of recursion:
Decomposition: decompose the original problem into several small-scale, independent subproblems with the same form as the original problem
Solution: if the subproblem is small and easy to be solved, solve it directly, otherwise solve each subproblem recursively
Merge: merge the solutions of each sub problem into the solutions of the original problem.

Example: Interview question 08.06 Hanoi Tower problem

What I did: (no, I didn't find out what was wrong)

    public static void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
        move(A,B,C);
    }

   public static void move(List<Integer> A, List<Integer> B, List<Integer> C){
        if(A.size() == 2){
            B.add(A.remove(1));
            C.add(A.remove(0));
            C.add(B.remove(0));
            return;
        }
       move(A.subList(1,A.size()),C,B);
       C.add(A.remove(0));
       move(B,A,C);
   }

Others solution:

public static void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
    move(A.size(), A, B, C);
}

private static void move(int n, List<Integer> a, List<Integer> b, List<Integer> c) {
    if (n == 0) return;
    move(n - 1, a, c, b);
    c.add(a.get(a.size() - 1));
    a.remove(a.size() - 1);
    move(n - 1, b, a, c);
}

dynamic programming algorithm

The core idea of dynamic programming algorithm is to divide large problems into small problems to solve, so as to obtain the optimal solution step by step

Dynamic programming algorithm is similar to divide and conquer algorithm. Its basic idea is to decompose the problem to be solved into several subproblems. First solve the subproblems, and then get the solution of the original problem from the solutions of these subproblems.

Different from the divide and conquer method, the sub problems obtained by decomposition are often not independent of each other. (that is, the solution of the next sub stage is based on the solution of the previous sub stage for further solution)

Dynamic programming can be advanced step by step by filling in tables to obtain the optimal solution

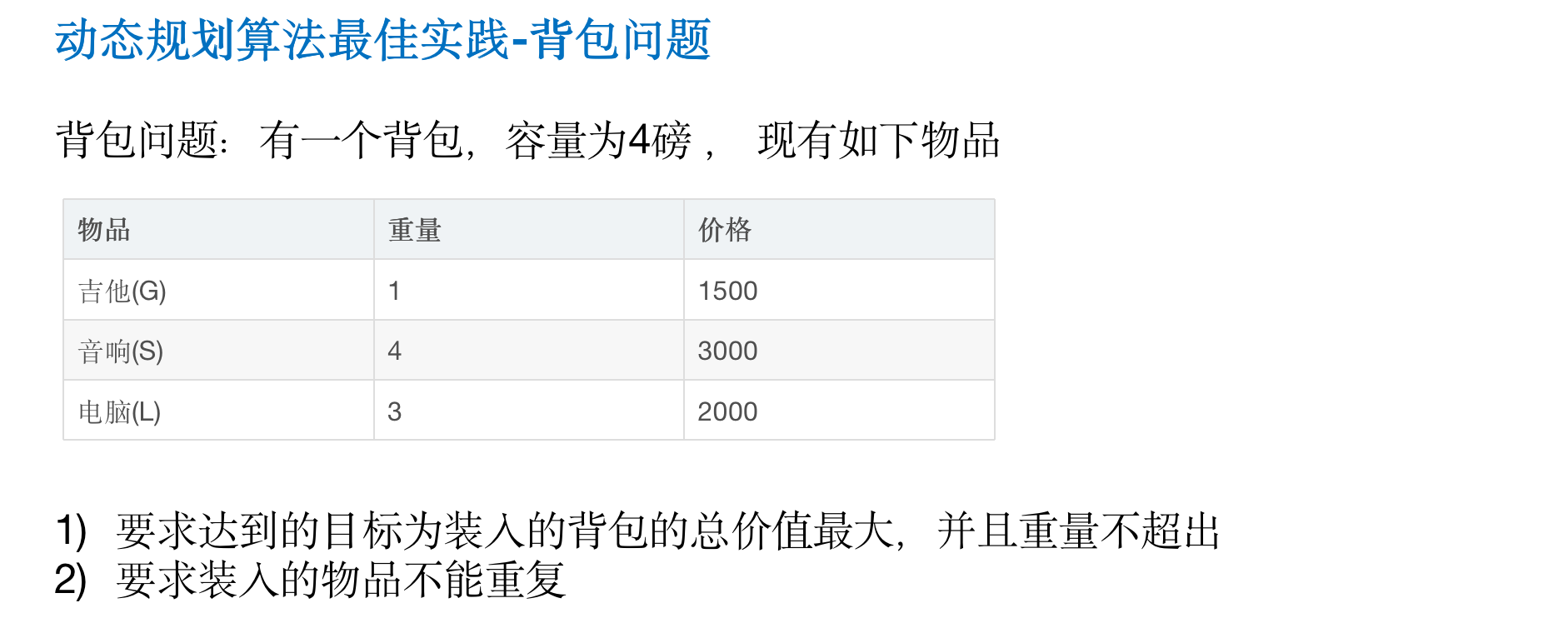
The main idea of the algorithm is solved by dynamic programming. For the i-th item traversed each time, determine whether to put the item into the backpack according to w[i] and v[i]. That is, for a given n items, let v[i] and w[i] be the value and weight of the ith item respectively, and C be the capacity of the backpack. Let v[i][j] represent the maximum value that can be loaded into the backpack with capacity j in the first I items. Then we have the following results: (1) v[i][0]=v[0][j]=0// Indicates that the first row and the first column of the filled table are 0
(2) When w [i] > J: v[i][j]=v[i-1][j] / / when the capacity of the new item to be added is greater than the capacity of the current backpack, the loading strategy of the previous cell is directly used
(3) When J > = w [i]: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}

v[i-1][j]: the maximum value of the previous cell
v[i]: indicates the value of the current commodity
v[i-1][j-w[i]]: load i-1 goods to the maximum value of the remaining space j-w[i]
When J > = w [i]: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}

Solution:

public class KnapsackProblem {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] w = {1, 4, 3};
		int[] val = {1500, 3000, 2000}; 
		int m = 4;
		int n = val.length; 
		
		
		
		int[][] v = new int[n+1][m+1];
		int[][] path = new int[n+1][m+1];
		
		for(int i = 0; i < v.length; i++) {
			v[i][0] = 0; 
		}
		for(int i=0; i < v[0].length; i++) {
			v[0][i] = 0; 
		}
		
	
		for(int i = 1; i < v.length; i++) { 
			for(int j=1; j < v[0].length; j++) {
				if(w[i-1]> j) { 
					v[i][j]=v[i-1][j];
				} else {
					if(v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) {
						v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
						path[i][j] = 1;
					} else {
						v[i][j] = v[i - 1][j];
					}
					
				}
			}
		}
		
	
		for(int i =0; i < v.length;i++) {
			for(int j = 0; j < v[i].length;j++) {
				System.out.print(v[i][j] + " ");
			}
			System.out.println();
		}
		
		System.out.println("============================");
		
		int i = path.length - 1; 
		int j = path[0].length - 1; 
		while(i > 0 && j > 0 ) { 
			if(path[i][j] == 1) {
				System.out.printf("Goods put into Backpack\n", i); 
				j -= w[i-1]; 
			}
			i--;
		}
		
	}
}

KMP algorithm

Application scenario - string matching problem
String matching problem:
There is a string str1 = "ABCBDCE" and a substring str2 = "BDC"
Now it is necessary to determine whether str1 contains str2. If it exists, it returns the first occurrence position. If not, it returns - 1

Introduction to KMP algorithm
The KMP algorithm uses the previously judged information to save the length of the longest common subsequence in the pattern string through a next array. During each backtracking, the previous matching position is found through the next array, saving a lot of calculation time
reference material: https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html

public class KMPAlgorithm {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		String str1 = "BBC ABCDAB ABCDABCDABDE";
		String str2 = "ABCDABD";
		//String str2 = "BBC";
		
		int[] next = kmpNext("ABCDABD"); //[0, 1, 2, 0]
		System.out.println("next=" + Arrays.toString(next));
		
		int index = kmpSearch(str1, str2, next);
		System.out.println("index=" + index); 
		
		
	}
	
	public static int kmpSearch(String str1, String str2, int[] next) {
		
		for(int i = 0, j = 0; i < str1.length(); i++) {
			while( j > 0 && str1.charAt(i) != str2.charAt(j)) {
				j = next[j-1]; 
			}
			
			if(str1.charAt(i) == str2.charAt(j)) {
				j++;
			}			
			if(j == str2.length()) {
				return i - j + 1;
			}
		}
		return  -1;
	}
	
	public static  int[] kmpNext(String dest) {
		int[] next = new int[dest.length()];
		next[0] = 0; 
		for(int i = 1, j = 0; i < dest.length(); i++) {
			
			while(j > 0 && dest.charAt(i) != dest.charAt(j)) {
				j = next[j-1];
			}		
			if(dest.charAt(i) == dest.charAt(j)) {
				j++;
			}
			next[i] = j;
		}
		return next;
	}
}