I. 01 knapsack problem
Title Description: There are n items with wi and vi weight and value respectively. From these items, items with total weight not exceeding W are selected, and the maximum value of the total value in all the selection schemes is obtained.
       1<=n<=100
       1<=wi,vi<=100
       1<=w<=10000
Examples:
input
       n=4
       (w,v)={(2,3),(1,2),(3,4),(2,2)}
       W=5
output
7 (Choose items 0, 1, 3)
Because there are only two cases of choosing and not choosing each item, the problem is called 01 knapsack.

Solution 1:
Idea analysis: This solution uses depth-first search, traversing each case, and selecting the maximum value. There are two kinds of deep search, one is to choose the current location, the other is not to choose the current location. The solution first calls a custom function, and then divides it into two cases. If not selected, the maximum weight W remains unchanged, and the optional position current+1. If selected, the maximum weight becomes W - w[current], and the optional position is current+1. Continue recursion. Then, in each recursive process, the largest of the two cases should be selected. Finally, we need to determine the export and output the results.

	static int W=5;												//Maximum weight
	static int n=4;												//Number of items
	static int[] w= {2,1,3,2};									//Weight of each object
	static int[] v= {3,2,4,2};									//The Value of Every Object
	
	public static void main(String[] args) {
		int x=f(W,0);											//Calling custom functions
		System.out.println(x);									//Output results
	}
	private static int f(int W, int current) {
		if (W <= 0) {													//Export judgment
			return 0;
		}
		if (current == n) {												//Export judgment
			return 0;
		}
		int value1 = f(W, current + 1);								   //Unselected cases
		if (W >= w[current]) {
			int value2 = v[current] + f(W - w[current], current + 1);	//Choose the current situation
			int temp = Math.max(value1, value2);						//Take a larger value of both.
			return temp;
		}
		return value1;
	}

Solution 2:
Idea analysis: In fact, the second solution is only a simple optimization of the first solution, so only some optimized annotations are marked. The optimization is that there are duplicates in every recursion, so a memory array is created to record the values in the previous recursion. Memory array is a two-dimensional array, arr [current location] [residual maximum multiplier weight]. Memory arrays need to be initialized and all positions set to - 1. In method invocation, if the value is greater than 0, it indicates that the value has been invoked before, and can be directly retrieved and returned.

	static int W=5;												//Maximum weight
	static int n=4;												//Number of items
	static int[] w= {2,1,3,2};									//Weight of each object
	static int[] v= {3,2,4,2};									//The Value of Every Object
	static int[][] arr=new int[n][W+1];							//Memory array					
	
	public static void main(String[] args) {
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < W + 1; j++) {
				arr[i][j] = -1;									//Initialize Memory Array
			}
		}
		int x = f(W, 0); 										// Calling custom functions
		System.out.println(x); 									// Output results
	}
	//Memory recursion
	private static int f(int W, int current) {
		if (W <= 0) {
			return 0;
		}
		if (current == n) {
			return 0;
		}
		if (arr[current][W] >= 0) {										//If the memory array contains values
			return arr[current][W];										//Take the value and return it directly
		}
		int value1 = f(W, current + 1);
		int value2 = 0;
		if (W >= w[current]) {
			value2 = v[current] + f(W - w[current], current + 1);
		}
		int judge = Math.max(value1, value2);							//Choose the larger values in both cases
		arr[current][W] = judge;										//Store in memory array
		return judge;
	}

Solution 3:
Idea analysis: This problem is solved by dp method. The blogger may not be able to describe the dp method clearly in language, so he needs to understand the principle first. This problem is solved by dp method. Excel table is needed. The first row represents the maximum load and the first column represents each item. The second row in the table needs to be initialized first, which is the first for loop in method f. Then traverse each line, there are two cases, the first case is not recommended, then directly select the larger value of the previous line. The second case is to take, and then use the value of Item i + the corresponding maximum load in the previous line. In fact, it means filling in the form until the last one is filled out, and the last one is the maximum. (The blogger has tried his best to describe it. i'm sorry if it doesn't make you understand.)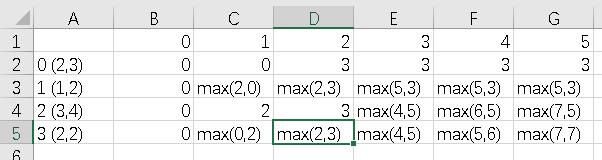

static int W=5;												//Maximum weight
	static int n=4;												//Number of items
	static int[] w= {2,1,3,2};									//Weight of each object
	static int[] v= {3,2,4,2};									//The Value of Every Object
	static int[][] arr=new int[n][W+1];							//Memory array					
	
	public static void main(String[] args) {
		int x = f(W, 0); 										// Calling custom functions
		System.out.println(x); 									// Output results
}
	//dp method
	private static int f(int W, int current) {
		for (int i = 0; i < W + 1; i++) {
			if (i >= w[0]) {
				arr[0][i] = v[0];								//Initialize the first line
			}	
		}
		for (int i = 1; i < n; i++) {
			for (int j = 0; j < W + 1; j++) {
				if (j >= w[i]) {
					arr[i][j] = Math.max(v[i] + arr[i - 1][j - w[i]], arr[i - 1][j]);	//Choose the larger values in both cases
				} else {
					arr[i][j] = arr[i - 1][j];						//There's only one case, direct deposit.
				}
			}
		}
		return arr[n - 1][W];
	}

2. Digital Triangle Problem
Title Description: Find a path from top to bottom in a digital triangle to maximize the sum of the numbers passing through the path. Every step on the path can only be left-down or right-down. Just ask for the maximum sum, not the path. The number of rows in a triangle is greater than 1, less than or equal to 100, and the number is between 0 and 99.
       1<=n<=100
       1<=wi,vi<=100
       1<=w<=10000
Examples:
input

output
30

Solution 1:
Idea analysis: This problem is also solved by deep search method. First, the custom function f1 is called, and the maximum number of rows of the triangle maxLength is obtained. If maxLength== row number i, it returns triangle[i][j] directly. Otherwise, the call continues recursively, with the value on (i,j) plus the maximum value of the next line, and returns. Final output

public static void main(String[] args) {
		int[][] triangle= {
				{7},
				{3,8},
				{8,1,0},
				{2,7,4,4},
				{4,5,2,6,5}
		};
		int temp=f2(triangle,0,0);								//Calling custom functions
		System.out.println(temp);
	}
	//dfs method
	public static int f1(int[][] triangle,int i,int j) {
		int maxLength=triangle.length;							//Number of rows in a triangle
		if(i==maxLength-1) {
			return triangle[i][j];								//Arrive at the last line and return directly
		}else {
			return triangle[i][j]+Math.max(f1(triangle,i+1,j), f1(triangle,i+1,j+1));	//Numbers on (i, j) bits plus larger values on the next line
		}
	}

Solution 2:
Train of thought analysis: this problem is solved by dp method. First of all, it's equivalent to building tables. First, initialize the last line of the triangle and store it in a new two-dimensional array. Then fill in from the penultimate line, each time selecting the larger value in the next. Till you finish the first line. The [0] [0] position in a two-dimensional array is the result.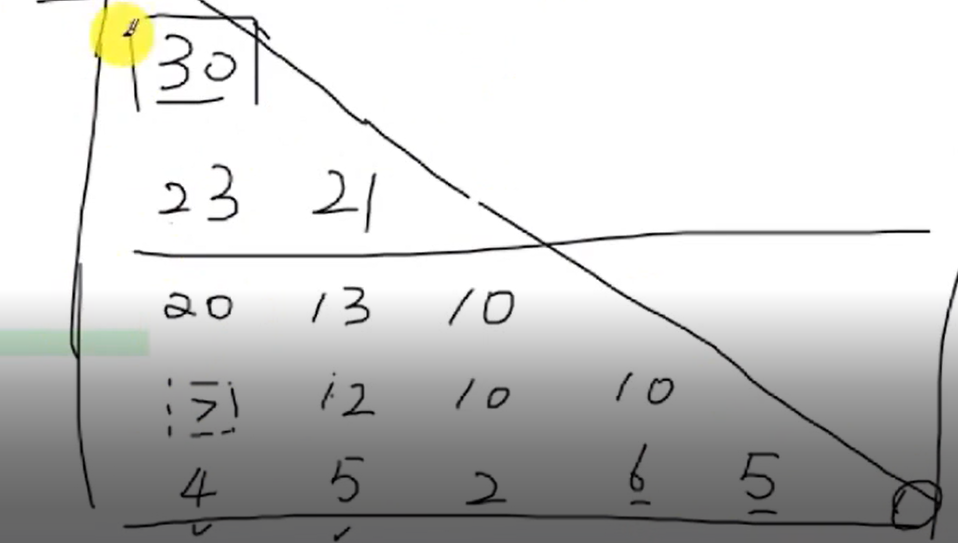

public static void main(String[] args) {
		int[][] triangle= {
				{7},
				{3,8},
				{8,1,0},
				{2,7,4,4},
				{4,5,2,6,5}
		};
		int temp=f2(triangle);								//Calling custom functions
		System.out.println(temp);
	}
	//dp method
		public static int f2(int[][] triangle) {
			int maxLenth=triangle.length;						//Get the maximum number of rows
			int[][] arr=new int[maxLenth][maxLenth];			//Create a new two-dimensional array
			for(int q=arr.length-1;q>=0;q--) {
				arr[maxLenth-1][q]=triangle[maxLenth-1][q];		//Initialize the last line of a two-dimensional array
			}
			for(int k=arr.length-2;k>=0;k--) {
				for(int c=0;c<=k;c++) {
					arr[k][c]=triangle[k][c]+Math.max(arr[k+1][c], arr[k+1][c+1]);	//Fill in from bottom to top and select the values on the larger number + (k,c) in the next line
				}
			}
			return arr[0][0];									//Return results
		}

3. Complete knapsack problem
Title Description: There are n items of weight and value of wi and vi respectively. From these items, items whose total weight is not more than W are selected to obtain the maximum value of the total value in all the selection schemes.
Examples:
      1<=n<=100
      1<=wi,vi<=100
      1<=W<=10000
input
n=5
(w,v)={(2,3),(1,2),(3,4),(2,2)}
output
10

Solution 1:
Idea Analysis: This reader can compare him with 01 knapsack. The difference between this question and the first one is that there is no limit on how many items there are, so you can choose more than one item. After analysis, as in the first question, there are two situations. In the first case, the value in arr[i-1][j] is taken directly. The second case is to take, then v[i]+arr[i][j-w[i]. Just like the previous question, fill in the form. You can initialize the first row and the first column first, then fill the form one by one, and the last one is the maximum.

public static void main(String[] args) {
		int answer=f();
		System.out.println(answer);
	}
	static int W=2;												//Maximum weight
	static int n=4;												//Number of items
	static int[] w= {2,1,3,2};									//Weight of each object
	static int[] v= {3,2,4,2};									//The Value of Every Object
	public static int f() {
		int[][] arr=new int[n][W+1];
		for(int i=0;i<W+1;i++) {
			arr[0][i]=i/w[0]*v[0];								//Initialize the first line
		}
		for(int i=0;i<n;i++) {
			arr[i][0]=0;										//Initialize the first column
		}
		for(int i=1;i<n;i++) {		
			for(int j=1;j<W+1;j++) {
				if(j>=w[i]) {									//If the weight of the item is less than the maximum load
				int temp1=arr[i-1][j];							//In the first case, the item is not taken.						
				int temp2=v[i]+arr[i][j-w[i]];					//In the second case, the item is not taken.
				arr[i][j]=Math.max(temp1, temp2);
				}else {											//otherwise
					arr[i][j]=arr[i-1][j];						//It is not taken directly.
				}
			}
		}
		return arr[n-1][W];
	}

4. The Problem of the Longest Rising Subsequence
** Title Description: Length of the Longest Incremental Subsequence
input
4 2 3 1 5 6
output
3 (because 235 makes up the longest incremental subsequence)

Solution 1:
Thought analysis: The first solution adopts a simple violent solution. In the function, the maximum length max=0 is initialized first. Then the two layers iterate through each character, and if the latter character is typed longer than the former, the length is + 1.

public static void main(String[] args) {
		int[] arr = { 4, 2, 3, 1, 5 };
		System.out.println(f(arr)); 						// Call custom functions
	}

	private static int f(int[] arr) {
		int max = 0;										//Maximum length of record
		for (int i = 0; i < arr.length; i++) {
			int p = i;										//Pointer, initialized to character i
			int cnt = 1;									//Initialization length is 1, because the number i is the first character
			for (int j = i + 1; j < arr.length; j++) {
				if (arr[j] > arr[p]) {								
					cnt++;									//Length plus one
					p = j;									//Change p to j
				}
			}
			if (cnt > max) {
				max = cnt;									//Change the maximum length
			}
		}
		return max;
	}

Solution 2:
Train of thought analysis: the second solution is dp solution. The idea here is to initialize a length number first, and set each position to 1, that is, at first each number is independent, so the length of a single number is 1. Then traverse each number. The second layer iterates through every number before the i-bit. If the number on the I-bit is larger than the number on the j-bit, the incremental sequence is formed. Therefore, the value of the length array J bit + 1 and the value of the length array I bit have been compared to the size, take a larger value. Finally, the length array is traversed and the result is output.

//dp method
	public static void main(String[] args) {
		int[] arr = { 4, 2, 3, 1, 5 };
		f(arr); 						// Call custom functions
	}
	public static void f(int[] arr) {
		int[] list=new int[arr.length];						//Create a new long array
		for(int i=0;i<list.length;i++) {		
			list[i]=1;										//First initialize each position to 1 (that is, only a single independent character)
		}
		for(int i=0;i<arr.length;i++) {						//Traveling through each number
			for(int j=i-1;j>=0;j--) {						//Traverse through each number before the number i
				if(arr[i]>arr[j]) {							//If the number of i digit is greater than that of j digit
					list[i]=Math.max(list[j]+1, list[i]);	//Comparing the maximum length of the number j + 1 with the maximum length of the number i, take a larger value.
				}
			}
		}
		int max=0;
		for(int i=0;i<list.length;i++) {
			if(list[i]>max) {
				max=list[i];								//Traverse the length array to get the maximum length
			}
		}
		System.out.println(max);
		
	}