Preface

• Language: Java
• Environment: IntelliJ IDEA
• JDK Version: 1.8
• Source code: GitHub

Overview of Search Algorithms and Efficiency Analysis

Algorithm name	Time complexity	Spatial complexity
Sequential search	O(n)	O(1)
Binary search	O(log2n)	O(1)
Interpolation search	O(log2(log2n))	O(1)
fibonacci search	O(log2n)	O(n)

In order to find

Algorithmic ideas:

• The value to be looked up is compared with the first data of the original array one by one.

Advantage:

• Data can be found in a disordered array.

Disadvantages:

• Because of its high time complexity, it is not suitable for searching from large amounts of data.

Code implementation:

    /**
     * Sequential lookup, returning only the index of the first number found
     * @param array Original array
     * @param key target value
     * @return  Finding an element returns its index, but not - 1.
     */
    public static int orderSearchOne(int[] array,int key){
        for(int i = 0;i<array.length;i++){  //Traversing arrays, comparing values
            if(array[i]==key){
                return i;   //Find the data and return the index
            }
        }
        return -1;
    }

    /**
     * Sequential lookup, returning all indexes found
     * @param array Original array
     * @param key target value
     * @return  Return a List. If the data is found, the index is put into the List and returned. If the data is not found, the empty List is returned.
     */
    public static List<Integer> orderSearchAll(int[] array, int key){
        List<Integer> list = new ArrayList<Integer>();
        for(int i = 0;i<array.length;i++){  //Traversing arrays, comparing values
            if(array[i]==key){
                list.add(i);    //Find the data and put the index in the list
            }
        }
        return list;
    }

Binary Search

Algorithmic ideas:

• The data in the array must be ordered.
• Find the median index mid=(low+high)/2 of the original array.
• Comparing the value to be searched with the median value, if it is equal to the median value, the index is returned; if it is less than or greater than the median value, the median value is continued to be calculated from the left or right part of the median value for searching until the median value is equal to the value to be searched, then the index is returned.
• If the value to be found is not found, the return value needs to be processed.

Advantage:

• Fast query speed

Disadvantages:

• Requiring the tables to be looked up as ordered tables and difficult to insert and delete
• Half-fold lookup method is only applicable to lookup frequent sequential tables with infrequent changes.

Non-recursive code implementation:

    /**
     * Half search (non-recursive), returning only the index of the first number found
     * @param array Original array
     * @param key target value
     * @return Finding an element returns its index, but not - 1.
     */
    public static int binarySearchOne(int[] array,int key){
        int low = 0;
        int high = array.length-1;
        if (key<array[low]||key>array[high]){   //Inquiry data is out of scope, return - 1
            return -1;
        }
        while (low<=high){
            int mid = (low+high)/2; //Get the intermediate index
            if(key<array[mid]){   //If the target value is less than the intermediate value, look in the left
                high = mid - 1;
            }
            if (key>array[mid]){  //If the target value is greater than the median value, look in the right part
                low = mid + 1;
            }
            if(key==array[mid]){  //If the intermediate value equals the target value, the index is returned
                return mid;
            }
        }
        return -1;
    }

    /**
     * Half-way lookup (non-recursive), returning all indexes found
     * @param array Original array
     * @param key target value
     * @return Return a List. If the data is found, the index is put into the List and returned. If the data is not found, the empty List is returned.
     */
    public static List<Integer> binarySearchAll(int[] array,int key){
        int low = 0;
        int high = array.length-1;
        List<Integer> list = new ArrayList<Integer>();
        if (key<array[low]||key>array[high]){   //Inquiry data is out of scope, return empty list
            return list;
        }
        while (low<=high){
            int mid = (low+high)/2; //Get the intermediate index
            if (key<array[mid]){   //If the target value is less than the intermediate value, look in the left
                high = mid - 1;
            }
            if (key>array[mid]){  //If the target value is greater than the median value, look in the right part
                low = mid + 1;
            }
            if(key==array[mid]){  //If the intermediate value equals the target value, place the intermediate index in the list and look around for the index
                list.add(mid);
                int temp = mid+1;   //Auxiliary index, since half-search is done in an ordered array, after querying a matching index, the other locations are on the adjacent left and right sides of the mid.
                while(temp<array.length&&array[temp]==key){   //Query on the right
                    list.add(temp);
                    temp++;
                }
                temp = mid-1;
                while(temp>0&&array[temp]==key){  //Left query
                    list.add(temp);
                    temp--;
                }
                break;  //Exit loop
            }
        }
        return list;
    }

Recursive code implementation:

    /**
     * Half search (recursion) returns only the index of the first number found
     * @param array Original array
     * @param key target value
     * @param low  Initial Index of Query Array
     * @param high Array End Index of Queries
     * @return Finding an element returns its index, but not - 1.
     */
    public static int binarySearchOne(int[] array,int key,int low,int high){
        int mid = (low+high)/2; //Get the intermediate index
        if(low>high||key<array[low]||key>array[high]){   //If no data is queried, or the query data is out of scope, return - 1
            return -1;
        }
        if(key<array[mid]){   //If the target value is less than the intermediate value, recurse to the left
            return binarySearchOne(array,key,low,mid-1);
        }
        if(key>array[mid]){   //If the target value is greater than the median value, recurse to the right
            return binarySearchOne(array,key,mid+1,high);
        }
        return mid; //If the target value equals the intermediate value, return the index
    }

    /**
     * Half Search (Recursive), returning all indexes found
     * @param array Original array
     * @param key target value
     * @param low  Initial Index of Query Array
     * @param high Array End Index of Queries
     * @return Return a List. If the data is found, the index is put into the List and returned. If the data is not found, the empty List is returned.
     */
    public static List<Integer> binarySearchAll(int[] array,int key,int low,int high){
        int mid = (low+high)/2; //Get the intermediate index
        if(low>high||key<array[low]||key>array[high]){    //If no data is queried, or the query data is out of scope, return an empty list
            return new ArrayList<Integer>();
        }
        if(key<array[mid]){   //If the target value is less than the intermediate value, recurse to the left
            return binarySearchAll1(array,key,low,mid-1);
        }
        if(key>array[mid]){   //If the target value is greater than the median value, recurse to the right
            return binarySearchAll1(array,key,mid+1,high);
        }
        List<Integer> list = new ArrayList<Integer>();  //Create a list to store the index found
        list.add(mid);  //The median is equal to the target value, and the index is placed in the list.
        int temp = mid+1;   //Auxiliary index, since half-search is done in an ordered array, after querying a matching index, the other locations are on the adjacent left and right sides of the mid.
        while(temp<array.length&&array[temp]==key){   //Query on the right
            list.add(temp);
            temp++;
        }
        temp = mid-1;
        while(temp>0&&array[temp]==key){  //Left query
            list.add(temp);
            temp--;
        }
        return list;
    }

Interpolation Search

Algorithmic ideas:

• The data in the array must be ordered.
• The idea of the algorithm is the same as the half-search, but the method of determining the index of the median value is different.
• Interpolation lookup determines the intermediate index mid= (high-low)* (key-array [low]/(array [high]-array [low]) +low

Formula deduction:

1. Let the first index of array be low and the last index be high. The value to be searched is key and the middle index is mid.
2. Because the array is ordered, the proportion of key in the original array value can be calculated:

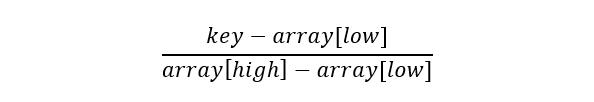
1. In our opinion, the proportion of the numerical value is approximately the same as that of the index where the key is located and that of the total index, while the index of the key is the mid we expect, the following equation can be obtained:

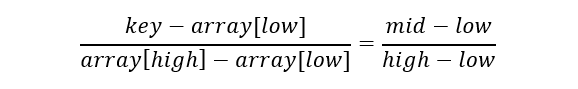
1. After deformation:

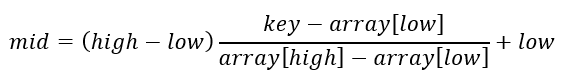
Advantage:

• Fast query speed
• For arrays with uniform keyword distribution, query speed will be better than half search. If the distribution of keywords is not uniform, the query speed is similar to the half-search speed.

Disadvantages:

• Requiring the tables to be looked up as ordered tables and difficult to insert and delete
• Interpolation lookup method is only applicable to lookup frequent sequential tables without frequent changes.

Fibonacci Search

Algorithmic ideas:

• The data in the array must be ordered.
• The idea of the algorithm is the same as the half-search, but the method of determining the index of the median value is different.
• The number of elements in the original array is expressed by the value of the Fibonacci sequence. For example, if the original array has eight elements, then the Fibonacci sequence is used to segment the array. There are five elements in the left part and three elements in the right part. mid=4.
• The actual representation is shown in the following figure, where k is the K item of the Fibonacci sequence and F is the Fibonacci sequence:

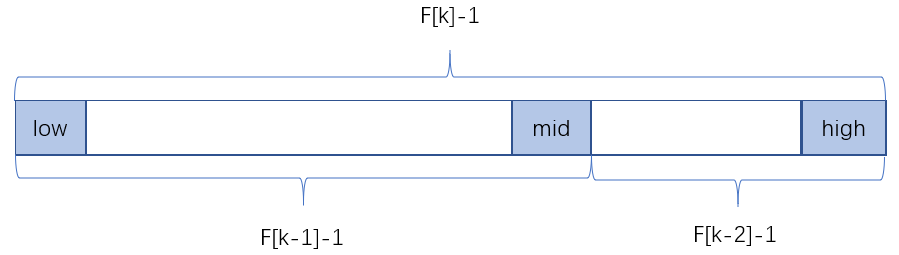
• We need to calculate the value of k and adjust the length of the original array to the value in the Fibonacci sequence.

Advantage:

• Fast query speed
• Unlike interpolation queries, Fibonacci queries are not affected by numerical values
• Query speed is better than half-fold search

Disadvantages:

• Requiring the tables to be looked up as ordered tables and difficult to insert and delete
• Fibonacci lookup method is only applicable to lookup frequent sequential tables with infrequent changes.
• Because the algorithm needs to adjust the length of the original array, in order not to change the original array, it needs auxiliary array, which will consume space resources.

Code implementation:

    /**
     * Fibonacci lookup, returning only the index of the first number found
     * @param array Original array
     * @param key target value
     * @return Finding an element returns its index, but not - 1.
     */
    public static int fibonacciSearch(int[] array,int key){
        int low = 0;
        int high = array.length-1;
        int n = 0;  //The n-th Value of the Marked Fibonacci Sequence
        int[] f = null; //Array with n+1 items (i.e. containing n items)
        int[] temp = null;  //Auxiliary array when filling an array, in order not to modify the original array data
        while (array.length>fibonacci(n)){  //Calculating the value of n requires that the value of n must be greater than or equal to the length of the array.
            n++;
        }
        f = getFibonacci(n);    //Generating Fibonacci array
        if(array.length<f[n]){  //If the length of the original array is less than the value of item n, the original array needs to be filled in
            temp = Arrays.copyOf(array,f[n]);   //Copy the original array data to temp and the length is f[n]
            for(int i = high+1;i<f[n];i++){ //Fill in the extra index bits with the last data value of the original array
                temp[i] = array[high];
            }
        }
        while (low<=high){  //Similar to half-look-up, mid only takes a different value
            int mid = low+f[n-1]-1; //Get the intermediate index
            if(key<temp[mid]){   //If the target value is less than the intermediate value, look in the left
                high = mid - 1;
                n -= 1;
            }
            if (key>temp[mid]){  //If the target value is greater than the median value, look in the right part
                low = mid + 1;
                n -= 2;
            }
            if(key==temp[mid]){  //If the intermediate value equals the target value, the index is returned. Note that the queried index cannot be a filled value index.
                if(mid<high){
                    return mid;
                }else{  //If the value of mid is greater than high, it means that the filled value is queried and returned high.
                    return high;
                }
            }
        }
        return -1;

    }
    /**
     * Get the nth value of Fibonacci sequence, n starts at 0.
     */
    private static int fibonacci(int n){
        if(n<0){
            return -1;
        }
        if(n == 0||n == 1){
            return 1;
        }
        return fibonacci(n-1)+fibonacci(n-2);
    }

    /**
     * Gets a Fibonacci sequence from zero to n with an array length of n+1
     */
    private static int[] getFibonacci(int n){
        int[] fib = new int[n+1];
        fib[0] = fib[1] = 1;
        for(int i = 2;i<=n;i++){
            fib[i] = fib[i-1]+fib[i-2];
        }
        return fib;
    }