aggregate
Into an array with neither repeating elements nor the concept of order. Represented by object {}.
function Set(){
var items={};
//Add a new item to the collection. true indicates that this value is added. If the value already exists in the collection, false is returned, indicating that it has not been added.
this.add=function(value){
if(!this.has(value)){
items[value]=value;
return true;
}
return false;
}
//Removes a value from the collection.
this.remove=function(value){
if(items[value]){
delete items[value];
return true;
}
return false;
}
//Returns true if the value is in the collection, otherwise false.
this.has=function(value){
return return items.hasOwnProperty(value);
}
//Remove all items from the collection.
this.clear=function(){
items={};
}
//Returns the number of elements contained in the collection. Similar to the length attribute of an array.
this.size=function(){
return Object.keys(items).length;
}
//Returns an array containing all the values in the collection.
this.values=function(){
return Object.keys(items);
}
}Union
For a given two sets, returns a new set containing all the elements in both sets. Object. Assign(), both;
The mathematical concept of union, the union of sets A and B, expressed as A ∪ B, is defined as follows:
A∪B = { x | x ∈ A∨x ∈ B }
It means that x (element) exists in A, or X exists in B.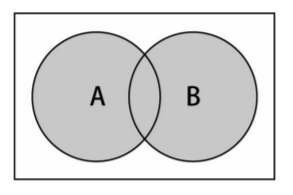
Now let's implement the union method of the Set class:
this.union = function(otherSet){
var unionSet = new Set();
var values = this.values();
for (var i=0; i<values.length; i++){
unionSet.add(values[i]);
}
values = otherSet.values();
for (var i=0; i<values.length; i++){
unionSet.add(values[i]);
}
return unionSet;
}; Test the above code:
var setA = new Set(); setA.add(1); setA.add(2); setA.add(3); var setB = new Set(); setB.add(3); setB.add(4); setB.add(5); setB.add(6); var unionAB = setA.union(setB); console.log(unionAB.values());
The output is ["1", "2", "3", "4", "5", "6"]. Note that element 3 exists in both A and B, and it appears only once in the set of results.
intersection
For a given two sets, returns a new set containing elements common to both sets. As long as you have it at the same time.
The mathematical concept of intersection, the intersection of sets A and B, expressed as A ∩ B, is defined as follows:
A∩B = { x | x ∈ A∧x ∈ B }
It means that x (element) exists in A and X exists in B.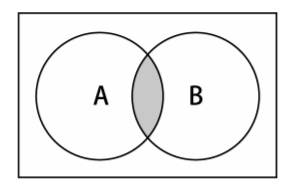
Now let's implement the intersection method of the Set class:
this.intersection = function(otherSet){
var intersectionSet = new Set(); //Both include
var values = this.values();
for (var i=0; i<values.length; i++){
if (otherSet.has(values[i])){
intersectionSet.add(values[i]);
}
}
return intersectionSet;
} Difference set
For a given two sets, returns a set containing all that exists in the first set and does not exist in the second set
A new collection of combined elements. As long as it is different from others.
The mathematical concept of difference set, the difference set of sets a and B, expressed as A-B, is defined as follows:
A-B = { x | x ∈ A ∧ x B }
It means that x (element) exists in A and X does not exist in B.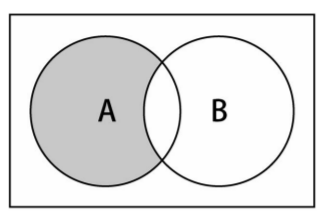
Now let's implement the difference method of the Set class:
this.difference = function(otherSet){
var differenceSet = new Set();//If A exists and B does not exist, the same data A.length > b.length will have A value, [1,2,3,4] - [1,2,3] = 4;
var values = this.values();
for (var i=0; i<values.length; i++){
if (!otherSet.has(values[i])){
differenceSet.add(values[i]);
}
}
return differenceSet;
};subset
Verifies whether a given set is a subset of another set. Judge that the subset must be the parent set.
The mathematical concept of subset. Set A is A subset of B (or set B contains
A), expressed as a ⊆ B, is defined as follows:
∀x { x ∈ A → x ∈ B }
It means that every x (element) in set A also needs to exist in B.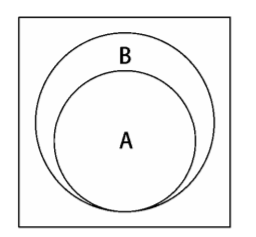
Now let's implement the subset method of the Set class:
this.subset = function(otherSet){
if (this.size() > otherSet.size()){
return false;
} else {
var values = this.values();
for (var i=0; i<values.length; i++){
if (!otherSet.has(values[i])){
return false;
}
}
return true;
}
}; Dictionaries
Collections, dictionaries, and hash tables can store non repeating values. In the dictionary, stored is [key, value]
Yes, where the key name is used to query specific elements. Dictionaries are also called mappings.
function Dictionary(){
var items={};
this.set=function(key,value){
items[key]=value;
}
this.remove=function(key){
if(this.has(key)){
delete items[key];
return true;
}
return false;
}
this.has=function(key){
return key in items;
}
this.get=function(key){
return this.has(key)?items[key]:undefined;
}
this.clear=function(){
items={};
}
this.size=function(){
return Object.keys(items).length;
}
this.keys=function(){
return Object.keys(items);
}
this.values=function(){
let values=[];
for(let key in items){
if(this.has(key)){
values.push(items[key])
}
}
return values;
}
this.getItems = function() {
return items;
}
}Hash table
HashTable class, also known as HashMap class, is a hash table of Dictionary class
Present mode. Use array mode.
The function of hash algorithm is to find a value in the data structure as soon as possible. Dao Ruo
To get a value in the data structure (using the get method), you need to traverse the entire data structure to find it. If hashing is used
Function, you know the specific location of the value, so you can quickly retrieve the value. The hash function is to give a key value and then return the address of the value in the table.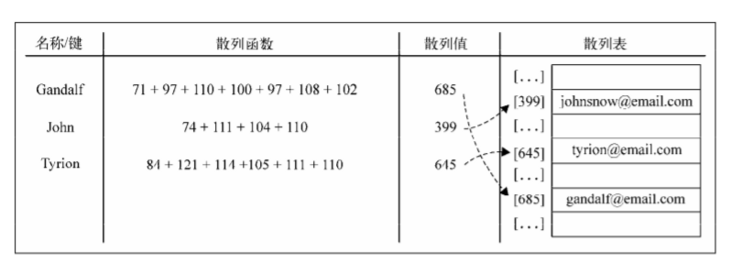
First implement a hash function, which is the private method of HashTable class, to obtain the ASCII value of each letter and a number in each key value.
let loseloseHashCode=function(key){
let hash=5381;
for(let i=0;i<key.length;i++){
hase=hash*33+key.charCodeAt(i);
}
return hash%1013;//1013 is an arbitrary prime number, let the value not be so large
}`function HashTable(){
let table=[];
this.put=function(key,value){
let position=loseloseHashCode(key);
table[position]=value;
}
this.remove=function(key){
table[loseloseHashCode(key)]=undefined;
}
this.get=function(key){
return table[loseloseHashCode(key)]
}}`
tree
Non sequential data structure - tree, which is very useful for storing data that needs to be searched quickly.
A tree structure contains a series of nodes with parent-child relationship. Each node has a parent node (except the first at the top)
Node) and zero or more child nodes: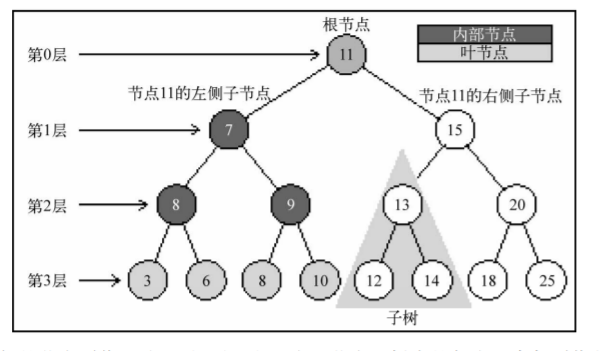
The node at the top of the tree is called the root node (11). It has no parent node. Each element in the tree is called a node
For internal and external nodes. A node with at least one child node is called an internal node (7, 5, 9, 15, 13 and 20 are internal nodes)
Node). Nodes without child elements are called external nodes or leaf nodes (3, 6, 8, 10, 12, 14, 18, and 25 are leaf nodes).
A node can have ancestors and descendants. The ancestors of a node (except the root node) include parent node, grandfather node and great ancestor
Parent node, etc. Descendants of a node include child nodes, grandson nodes, great grandson nodes, etc. For example, the ancestor of node 5 has node 7
And node 11, and the descendants have node 3 and node 6
Binary tree
A node in a binary tree can only have two child nodes at most: one is the left child node and the other is the right child node. These fixed
Meaning helps us write more efficient algorithms for inserting, finding and deleting nodes into / from trees. Application of binary tree in Computer Science
It is widely used.
Binary search tree (BST) is a kind of binary tree, but it only allows you to store smaller values in the left node (than the parent node),
A value larger (or equal to) than the parent node is stored in the right node.;
let insertNode=function(node,newNode){
//When you are young, you will find your subordinates on the left. The same is true on the right
if(newNode.key<node.key){
if(node.left===null){
node.left=newNode;
}else{
insertNode(node.left,newNode)
}
}else{
if(node.right===null){
node.right=newNode;
}else{
insertNode(node.right,newNode);
}
}
}function BinarySearchTree(){
let Node=function(key){
this.key=key;
this.left=null;
this.right=null;
}
let root=null;
this.insert=function(key){
let newNode=new Node(key);
if(root===null){
root=newNode;
}else{
insertNode(root,newNode);
}
}
this.search=function(key){
}
this.inOrderTraverse=function(callback){}
this.preOrderTraverse=function(){}
this.postOrderTraverse=function(){}
this.min=function(){}
this.max=function(){}
this.remove=function(key){
}
}Medium order traversal
Medium order traversal is a way to access all nodes of the BST in the order of more than one row, that is, in the order from the smallest to the largest
Ask all nodes. One application of medium order traversal is to sort the tree.
First, check whether the node passed in as a parameter is null (this is true)
Is the judgment condition for stopping recursive execution -- the basic condition of recursive algorithm).
Then, the same function is called recursively to access the child node on the left. Then do some operations on this node
(callback), and then access the child node on the right
this.inOrderTraverse=function(callback){
inOrderTraverse(root,callback);
}let inOrderTraverseNode=function(node,callback){
if(node!==null){
inOrderTraverseNode(node.left,callback);
callback(node.key);
inOrderTraverseNode(node.right,callback);
}
}Access path to the inOrderTraverse method: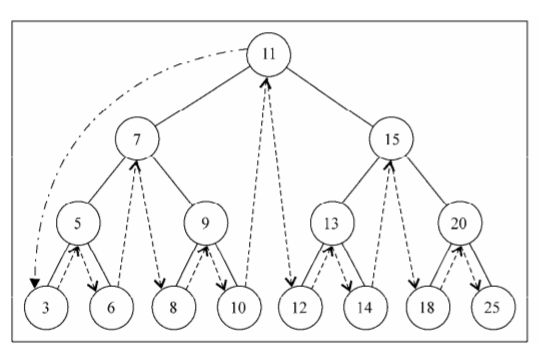
Preorder traversal
Preorder traversal accesses each node in the order of precedence over descendant nodes. One application of preorder traversal is to print a structure
Standardized documents.
The difference between preorder traversal and middle order traversal is that preorder traversal will first access the node itself, and then access its
The left child node is followed by the right child node.
this.preOrderTraverse=function(callback){
preOrderTraverseNode(root,callback)
}let preOrderTraverseNode=function(node,callback){
if(node!==null){
callback(node.key);
preOrderTraverseNode(node.left,callback);
preOrderTraverseNode(node.right,callbak);
}
}Access path of preOrderTraverse method: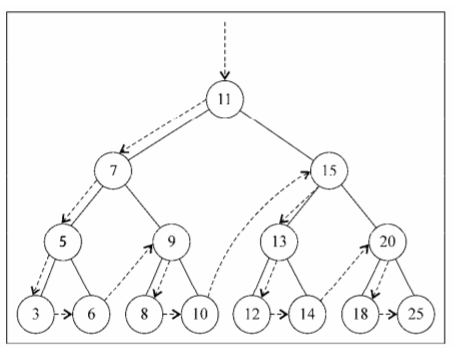
Postorder traversal
Postorder traversal is to access the descendant nodes of the node first, and then access the node itself. One application of postorder traversal is to calculate an object
The amount of space occupied by all files in the record and its subdirectories.
The postorder traversal will first access the left child node, then the right child node, and finally
Is the parent node itself
this.postOrderTraverse=function(callback){
postOrderTraverseNode(root,callback);
}let postOrderTraverseNode=function(node,callback){
if(node!==null){
postOrderTraverseNode(node.left,callback);
postOrderTraverseNode(node.right,callback);
callback(node.key);
}
}Access path of postOrderTraverse method: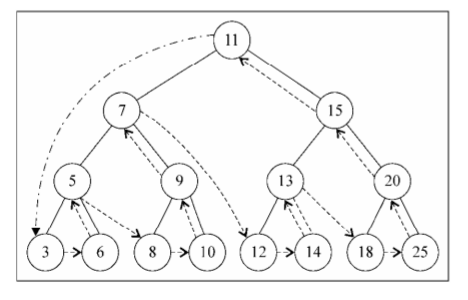
Search max min
The small one is on the left and the large one is on the right
this.min=function(){
return minNode(root);
}
let minNode=function(node){
if(node){
while(node&&node.left!==null){
node=node.left;
}
return node.key;
}
return null;
}this.max=function(){
return maxNode(root);
}
let maxNode=function(node){
if(node){
while(node&&node.right!==null){
node=node.right;
}
return node.key;
}
return null;
}Search for specific values
Return boolean;
this.search=function(key){
return searchNode(root,key);
}
let searchNode=function(node,key){
if(node===null){
return false;
}
if(key<node.key){
return searchNode(node.left,key);
}else if(key>node.key){
return searchNode(node.right,key);
}else{
return true;
}
}Remove a node
this.remove=function(key){
root=removeNode(root,key);
}
let removeNode=function(node,key){
if(node===null){
return null;
}
if(key<node.key){
node.left=removeNode(node.left,key);
}else if(key>node.key){
node.right=removeNode(node.right,key);
return node;
}else{//Key = node.key
//In the first case, a leaf node
if(node.left===null&&node.right===null){
node=null;
return node;
}
//In the second case, a node with only one child node
if(node.left==null){
node=node.right;
return node;
}else if(node.right===null){
node=node.left;
return node;
}
//In the third case, a node with 2 child nodes
let aux=findMinNode(node.right);
node.key=aux.key;
node.right=removeNode(node.right,aux.key);
return node;
}
}