catalog:
-
preface
-
Large number addition
-
Large number subtraction
-
Large number multiplication
-
Large number division
-
Factorial digits of large numbers
-
Factorial solution of large numbers
-
summary
1, Preface
As we all know, the length of computer data types is limited, so data overflow will occur when processing large data. At this time, we need to find a way to process this batch of data, so how do we deal with it? The answer is to use arrays to store data and then do batch processing.
I don't know if you have ever observed using recursion to calculate factorial. When n is 13 (the data type is int), the data is obviously wrong. A friend may say if it is long long data? longlong type data can certainly find more than 13, but more than 100? Did you cross the line again? Here I refer to the articles of other bloggers and write about the large number algorithm.
2, Text
1, Large number addition
The so-called large number addition is the addition operation when our computer data cannot store large data. How do we realize the addition of large numbers? We can use arrays, linked lists and other structures to store large data in segments. Here I use arrays to describe the operation of large numbers. If we input 123456789123456 + 123, if we want to add, how can we store the first number? The answer is to use an array to store, to be exact, a character array. We input these two characters as a string into a character array, and then reverse the order. Why reverse the order? For example, 123456789123456 + 123, here we add 6 and 3, 5 and 2, and 4 and 3, but is it inconvenient to express in the program? Another advantage is that we can carry out carry processing conveniently, so we use reverse order processing. How to reverse the order? Use the integer array to store the character array from the following table 0 - '0' (here we explain that the minus character 0 is to convert the character into the corresponding number. If you don't know, you can look up the Ascii code table). After the two arrays perform this operation in turn, you can add them with a sum array. The specific code is as follows:
#include "bits/stdc++.h"
#include "cstring"
using namespace std;
char s1[600],s2[600];
int a[600],b[600];
int sum[1200];
int main()
{
int i,j,res;
int length1,length2;
int len;
cin >> s1;
cin >> s2;
length1 = strlen(s1);
length2 = strlen(s2);
j = 0;
for(i = length1 - 1 ;i >= 0;i--)
a[j++] = s1[i] - '0';//Reverse
j = 0;
for(i = length2 - 1;i >= 0;i--)
b[j++] = s2[i] - '0';//Reverse
if(length1 > length2)
len = length1;//Traverse to the longest number
else
len = length2;
res=0;//Carry
for(i = 0;i < len;i++)
{
sum[i] = (a[i] + b[i] + res) % 10;
res = (a[i] + b[i] + res)/10;
}
if(res)//If carry still exists at this time
{
sum[i] = res;
i++;
}
for(j = i - 1;j >= 0;j--)
cout << sum[j];//Print from back to front
cout << endl;
return 0;
}
2, Large number subtraction
Large number subtraction uses the idea of large number addition to store data. When processing data, it starts from the low to the high. For example, after 123456 - 123 is reversed, it is 654321 - 321. At this time, 6 - 3,5 - 2,4-1, and then others can be directly assigned to the minus array. If the corresponding digit of the subtracted is less than the corresponding digit of the subtracted, we use the borrow method. For example, 1234-345, 4-5 < 0, forward borrowing, and the previous digit after borrowing is - 1, that is, 3-1 (here I default to the array after reversal). What if the subtraction is less than the subtraction? How do we judge? At this time, we only need to judge that if the length of the subtracted is less than the length of the subtracted, we can directly output a negative sign, and then use the subtraction subtracted. Someone asked again, what if the two digits are equal and the subtracted is less than the subtracted? At this time, we only need to traverse the reversed array from front to back. If the number of subtracted digits is less than the number of subtracted digits, I can judge it. Directly output a negative sign, and then subtract the subtracted number from the subtracted number. Generally speaking, the idea is that if the subtracted number is greater than the subtracted number, you can directly subtract it; If the subtracted number is less than the subtracted number, a negative sign is directly output, and then the subtracted number is subtracted from the subtracted number. For example, 123456 - 789123456 is a subtracted number, and 789 is a subtracted number. Don't get confused. Next, post my code implementation (the code is a little long, and capable partners can implement it by themselves):
#include "bits/stdc++.h"
using namespace std;
char s1[100],s2[100];
int length1,length2;
int a1[100],b2[100];
int i,j;
int len;
int minus1[200];
int main()
{
cin >> s1 >>s2;
length1 = strlen(s1);
length2 = strlen(s2);
j=0;//Add a1 array from scratch
for(i = length1 - 1;i >= 0;i--)
{
a1[j++] = s1[i] - '0';//inversion
}
j=0;//Add b array from scratch
for(i = length2 - 1;i >= 0;i--)
{
b2[j++] = s2[i] - '0';
}
len = (length1 > length2)?length1 : length2;//len is the longest of the two strings
if(length1 - length2 > 0)//First array minus second
{
for(i = 0;i < len;i++)
{
if(a1[i] >= b2[i])//If it is greater than, it will be reduced directly
minus1[i] = a1[i] - b2[i];
else
{
minus1[i] = a1[i] + 10 -b2[i];
a1[i+1] = a1[i+1] -1;
}
}
for(j = len -1;j >= 0;j--)//Because the lengths of the two numbers are different, the subtraction must not be 0, otherwise the last 0 must be retained
if(minus1[j] == 0)
len--;//Delete 0
else
break;
}
else if(length1 - length2 < 0)//Second array minus first
{
cout << "-";//Output negative sign
for(i = 0;i < len;i++)
{
if(b2[i] >= a1[i])//If it is greater than, it will be reduced directly
minus1[i] = b2[i] - a1[i];
else
{
minus1[i] = b2[i] + 10 -a1[i];
b2[i+1] = b2[i+1] -1;
}
}
for(j = len -1;j >= 0;j--)//Because the lengths of the two numbers are different, the subtraction must not be 0, otherwise the last 0 column must be retained, such as 99-100
if(minus1[j] == 0)
len--;//Delete 0
else
break;
}
else//If equal, judge who is big and who is small
{
for(i = len - 1;i >= 0;i--)
{
if(a1[i] == b2[i])
continue;
else if(a1[i] > b2[i])
break;
else
break;
}
if(a1[i] > b2[i])
{
for(i = 0;i < len;i++)
{
if(a1[i] >= b2[i])//If it is greater than, it will be reduced directly
minus1[i] = a1[i] - b2[i];
else
{
minus1[i] = a1[i] + 10 -b2[i];
a1[i+1] = a1[i+1] -1;
}
}
for(j = len -1;j >= 0;j--)//Because the lengths of the two numbers are different, the subtraction must not be 0, otherwise the last 0 must be retained
if(minus1[j] == 0)
len--;//Delete 0
else
break;
}
else if(a1[i] < b2[i])
{
cout << "-";//Output negative sign
for(i = 0;i < len;i++)
{
if(b2[i] >= a1[i])//If it is greater than, it will be reduced directly
minus1[i] = b2[i] - a1[i];
else
{
minus1[i] = b2[i] + 10 -a1[i];
b2[i+1] = b2[i+1] -1;
}
}
for(j = len -1;j >= 0;j--)//Because the lengths of the two numbers are different, the subtraction must not be 0, otherwise the last 0 column must be retained, such as 99-100
if(minus1[j] == 0)
len--;//Delete 0
else
break;
}
else
{
printf("0");
return 0;
}
}
for(j = len-1;j >= 0;j--)
cout << minus1[j];
cout << endl;
return 0;
}
3, Large number multiplication
I don't know whether my friends have understood the principle of calculator. I was lucky to know a book about the principle of calculator in the library, which introduces the four operations of calculator. The so-called multiplication is multiple addition. When we didn't understand multiplication in primary school, we would add 5 * 3 three times. In fact, this is the principle of multiplication, multiple accumulation. How can we implement it by program? For example, 123 * 45, after we reverse it to 321 * 54, 3 * 5 is 15, 1,3 * 4 is 12 tens, 2 * 5 is 10 tens, 2 * 4 is 8 hundreds, then 1 * 5 is 5 hundreds, 1 * 4 is 4 1000, and then carry the result. The specific code is as follows:
#include "bits/stdc++.h"
#include "cstring"
using namespace std;
char s1[100],s2[100];
int a1[100],b2[100];
int multi[200];
int main()
{
int i,j;
cin >> s1;
cin >> s2;
j = 0;
for(i = strlen(s1) - 1;i >= 0; i--)
a1[j++] = s1[i] - '0';
j = 0;
for(i = strlen(s2) - 1; i >= 0; i--)
b2[j++] = s2[i] - '0';//Flip number
for(i = 0;i < strlen(s1); i++)
for(j = 0;j < strlen(s2); j++)
{
multi[i + j] = multi[i + j] + a1[i] * b2[j];//Don't calculate carry first
}
for(i = 0;i < strlen(s1) + strlen(s2); i++)//The maximum number of digits multiplied by two numbers is the sum of two digits
if(multi[i] >= 10)
{
multi[i + 1] += multi[i] / 10;//Note that the array should be opened a little larger in advance, otherwise it will cross the boundary
multi[i] = multi[i] % 10;
}
for(i = strlen(s1) + strlen(s2) - 1;i >= 1; i--)//Delete redundant 0
if(multi[i] != 0)
break;
while(i >= 0)
{
cout << multi[i--];
}
cout << endl;
return 0;
}4, Large number division
#include "bits/stdc++.h"
#include "cstring"
using namespace std;
char s1[100],s2[100];
int a1[100],b1[100];
int len1,len2,len;//Len calculates the length of the difference between len1 and len2
int z[100];
int temp;
int subtraction(int length1,int length2)
{
int i;
for(i = 0;i < length2;i++)
{
if(a1[i] >= b1[i])
{
a1[i] -= b1[i];
}
else
{
a1[i] = a1[i] + 10 -b1[i];//If this number is less than, carry and subtract
a1[i + 1] -= 1;//Minus 1 after borrowing
}
}
for(i = length1;i > 0 && !a1[i];i--);//Prefix to eliminate divisor must start with length1
return i + 1;//i will judge every time, so add 1
}
int judge(int length1,int length2)
{
int i;
if(length1 < length2)
return -1;//Less than return - 1
else
{
for(i = len1 - 1;i >= 0;i--)
{
if(a1[i] == b1[i])
continue;
if(a1[i] < b1[i])//Less than - 1
return -1;
if(a1[i] > b1[i])//Greater than 1
return 1;
}
}
return 0;//Returns 0 if equal
}
int main()
{
int i,j;
cin >> s1;
cin >> s2;
len1 = strlen(s1);
len2 = strlen(s2);
if(len1 < len2)
{
cout << "consult: 0";
cout << "mod : ";
puts(s2);
}
else
{
for(i = len1 - 1,j = 0;i >= 0;i--)
{
a1[j++] = s1[i] - '0'; //Inverted array debugging succeeded
}
for(i = len2 - 1,j = 0;i >= 0;i--)
{
b1[j++] = s2[i] - '0'; //Inverted array debugging succeeded
}
len = len1 - len2;
for(i = len1 -1 ;i >= 0;i--)
if(i >= len)
b1[i] = b1[i-len];
else
b1[i] = 0;
len2 = len1;//Synchronous character digit debugging succeeded
for(j = 0;j <= len;j++)//This step is mainly to deal with the data on each bit
{
z[len - j] = 0;
while((temp = judge(len1,len2)) >= 0)
{
z[len - j]++;//If satisfied, it can be added once
len1 = subtraction(len1,len2);
cout << len1 << " " << j << endl;
cout << a1[0] << " " << a1[1] << endl;
}
if(temp < 0 && b1[0] == 0)//The divisor minus 1 can end if the prefix is not 0
{
for(i = 0;i < len2 - 1;i++)
{
b1[i] = b1[i + 1];
}
b1[len2 - 1] = 0;
len2--;//Reduce divisor digit
}
}
}
for(i = len;i > 0;i--)
{
if(z[i])
break;//Eliminate prefix 0 of quotient
}
cout << "consult:";
while(i >= 0)
cout << z[i--];
cout << endl;
cout << "mod:";
for(i = len1 - 1;i > 0;i--)
{
if(a1[i])
break;//Eliminate prefix 0 of quotient
}
if(len1 == 0)
i = len1;
while(i >= 0)
cout << a1[i--];
cout << endl;
return 0;
}5, Factorial digits of large numbers
I don't know if my little partner has ever used int type to calculate the factorial, he will find that the data is obviously wrong. For example, when we calculate the factorial of 13, we find that the factorial of print 13 is
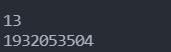
However, we can baidu search factorial calculator
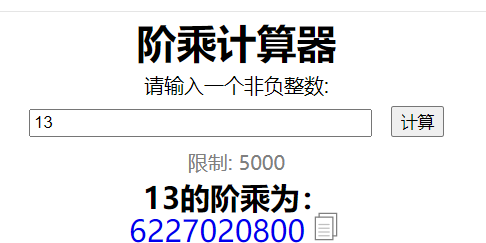
So what went wrong? The answer is that the length of the data type is not enough. Therefore, we should change the strategy, store data in an array, and then process it in batch. Next, we introduce two algorithms for calculating factorial digits. 1. Use logarithmic function to solve factorial digits
2. Use Stirling formula to solve the number of digits. Then introduce how to calculate factorial.
1. Find the number of digits with logarithmic function
lg1+lg2+lg3+lgn. According to the characteristics of logarithmic function, lga+lgb is equal to lga*b. at this time, we find that the real number a*b can be replaced by our 1 and 2-n. But why not cross the boundary at this time? Because the lg function returns a double type, we can save this value with a double type number. This value is small, so there will be no data overflow. It should be noted that the number of bits is initialized to 1. When outputting, the number of bits should be rounded and output. The specific codes are as follows:
#include "bits/stdc++.h"
#include "cmath"
using namespace std;
int main()
{
double sum = 0;
int i;
for(i = 1;i <= 200;i++)
sum += log10(i);//The number of factorial digits is calculated and judged by the characteristics of log10
cout << (int)(sum + 1) << endl;//sum starts with one digit
return 0;
}2. Calculation of digits by Stirling formula
The proof process of Stirling formula is complex. I'm just a chicken who remembers the formula. Please move to the boss's blog to think about it. Here is the link as follows https://www.cnblogs.com/jokerjason/p/9525590.html , here I post the code implementation
#include "bits/stdc++.h"
#include "cmath"
using namespace std;
const double e = 2.7182818284;//The more decimals, the higher the precision
const double Pi = 3.1415926535;
int main()
{
int res = 0;
int n;
cin >> n;
res = 0.5 * log10(2 * Pi * n) + n * log10(n/e);
cout << res + 1;
return 0;
}
6, Factorial solution of large numbers
The idea of factorial solution is to use an array to store, then enter a multiplier every time, and multiply each array element by this multiplier. If it is found that the high bit will overflow, we can add a high bit to store, and then deal with the carry problem. We still traverse from the low bit to the high bit. If it is greater than 10, we carry forward, Here I just use an array element to store 6 bits. Readers can use the 1-bit storage method to realize the factorial of large numbers. The specific codes are as follows:
#include "stdio.h"
int main()
{
int i = 1,high = 0,tag = 0;//tag is low, high is high, and i is factorial
int a[1000] = {0};//The calculation accuracy is 7000 bits
a[high] = 1;//Assign the initial value of the first operation to 1
while(i <= 100)
{
for(tag = 0;tag <= high; tag++)
a[tag] *= i;
if(a[high] >= 1000000)
high += 1;
for(tag = 0;tag <= high; tag++)
{
if(a[tag] >= 1000000)
{
a[tag + 1] += a[tag] / 1000000;
a[tag] = a[tag] % 1000000;
}
}
i++;
}
tag = high;
while(high >= 0)
{
if(high == tag)
printf("%d",a[high]);
else
printf("%06d",a[high]);//This is an output trick. Fill 0 on the left and - 06d on the right
high--;
}
return 0;
}7, Summary
The first time I published a blog, please point out the bad things in time, and I will modify them! In addition, learning is a very fulfilling and happy thing. Come on!