Dictionary tree
Concept of dictionary tree
This section is mainly for reference Reference link
Dictionary tree is also called Trie tree and prefix tree. As the name suggests, it is a data structure that maintains strings.
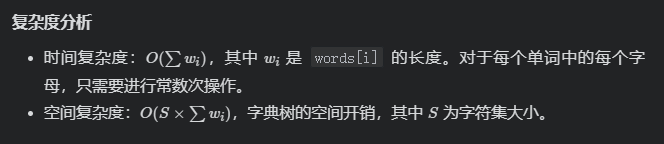
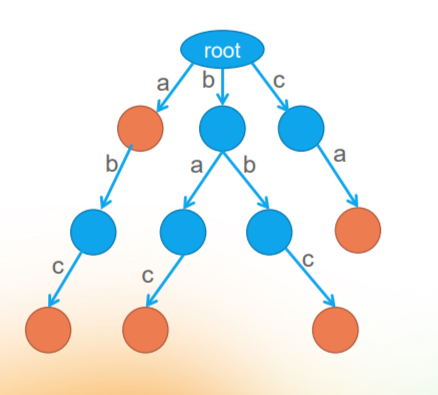
Dictionary tree, as the name suggests, is a tree about "dictionary". That is, it is a storage method for dictionaries (so it is a data structure rather than an algorithm). Each "word" in the dictionary is the path from the root node to a target node. The letters on each side of the path are connected to be a word.
(the node marked in orange is the "target node", that is, all letters on the path from the root node to the target node form a word.)
From this figure, we can see that the dictionary tree is a tree, but there is a letter on each side of the tree, and then some nodes of the tree are designated as marker nodes (target nodes).
This is the concept of dictionary tree. In combination with the above concepts, the dictionary tree shown in the figure above includes the following words:
a abc bac bbc ca
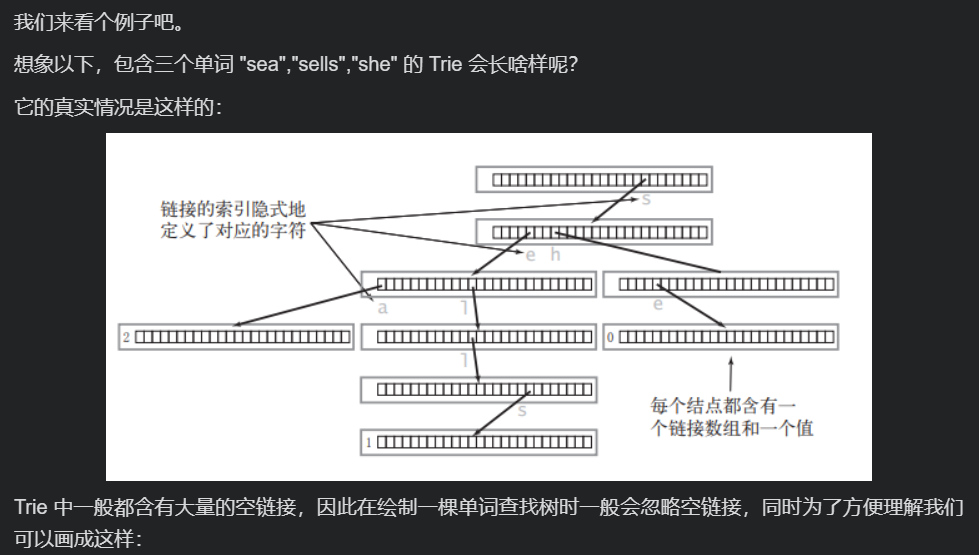
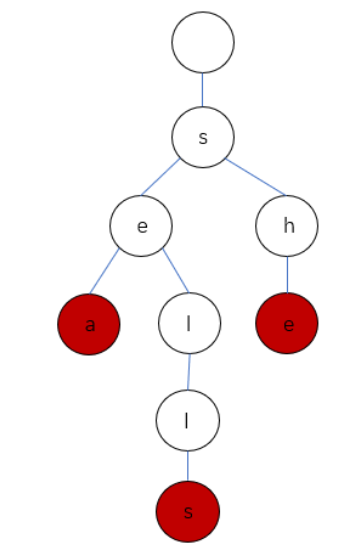
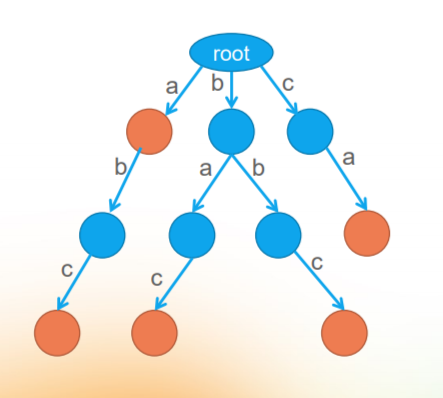
Functions of dictionary tree
According to the concept of dictionary tree, we can find that the essence of dictionary tree is to split many strings into the form of a single character and store them in the form of a tree. Therefore, we say that the dictionary tree maintains a "dictionary". According to this most basic property, we can extend many wonderful functions of the dictionary tree. A brief summary is as follows:
1. Maintain a collection of strings (that is, a dictionary).
2. Inserts a string (that is, builds a tree) into the string collection.
3. Query whether there is a string in the string collection (that is, query).
4. Count the number of strings in the collection (i.e. Statistics).
5. Sorts the string set in dictionary order (that is, dictionary order).
6. Find the LCP (Longest Common Prefix) of two strings in the set (that is, find the Longest Common Prefix).
We can find that the functions listed above are based on the "string set". Once again, the dictionary tree is a "dictionary" tree, and all functions are "dictionary" functions. This also provides a rule for us to use the dictionary tree: when we see a lot of strings appearing at the same time, think about the hash and Trie tree.
Implementation of dictionary tree and code implementation
The two basic operations of dictionary tree are tree building and query. The tree building operation is to insert a new word into the dictionary tree. The query operation is to query whether a given word is in the dictionary tree.
Trie is an atypical multi fork tree model, which is easy to understand, that is, the number of branches of each node may be multiple. Why atypical? This is because it is different from the general multitree, especially in the data structure design of nodes. For example, the nodes of the general multitree are as follows:
C++
struct TreeNode {
VALUETYPE value; //Node value
TreeNode* children[NUM]; //Point to child node
};
The node of Trie is like this (assuming that it only contains the characters in 'a' ~'z '):
C++
struct TrieNode {
bool isEnd; //Is this node the end of a string
TrieNode* next[26]; //Alphabet mapping table
};
Define class Trie:
C++
class Trie {
private:
bool isEnd;
Trie* next[26];
public:
//Method will be implemented below
};
Insert:
Description: insert a word word into Trie
Implementation: this operation is very similar to building a linked list. First, match the first character of word from the child node of the root node until there is no corresponding character on the prefix chain. At this time, continue to open up new nodes until the last character of word is inserted. At the same time, the last node isEnd = true;, Indicates that it is the end of a word.
C++
void insert(string word) {
Trie* node = this;
for (char c : word) {
if (node->next[c-'a'] == NULL) {
node->next[c-'a'] = new Trie();
}
node = node->next[c-'a'];
}
node->isEnd = true;
}
Find:
Description: find out if the word word word exists in Trie
Implementation: start from the child nodes of the root node and match downward. If the node value is empty, false will be returned. If the last character is matched, we just need to judge node - > Isend.
C++
bool search(string word) {
Trie* node = this;
for (char c : word) {
node = node->next[c - 'a'];
if (node == NULL) {
return false;
}
}
return node->isEnd;
}
Prefix match:
Description: judge whether there are words prefixed with prefix in Trie
Implementation: similar to the search operation, it is only unnecessary to judge the isEnd of the last character node, because since the last character can be matched, there must be a word prefixed with it.
C++
bool startsWith(string prefix) {
Trie* node = this;
for (char c : prefix) {
node = node->next[c-'a'];
if (node == NULL) {
return false;
}
}
return true;
}
At this point, we have realized some basic operations of Trie, so that we have a further understanding of Trie.
208. Implement Trie (prefix tree)
Trie (pronounced like "try") or prefix tree is a tree data structure used to efficiently store and retrieve keys in string data sets. This data structure has many application scenarios, such as automatic completion and spell checking.
Please implement the Trie class:
Trie() initializes the prefix tree object.
void insert(String word) inserts the string word into the prefix tree.
boolean search(String word) returns true if the string word is in the prefix tree (that is, it has been inserted before retrieval); Otherwise, false is returned.
boolean startsWith(String prefix) returns true if one of the prefixes of the previously inserted string word is prefix; Otherwise, false is returned.
Example:
input
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
output
[null, null, true, false, true, null, true]
explain
Trie trie = new Trie();
trie.insert("apple");
trie.search(“apple”); // Return True
trie.search(“app”); // Return False
trie.startsWith(“app”); // Return True
trie.insert("app");
trie.search(“app”); // Return True
Tips:
1 <= word.length, prefix.length <= 2000
word and prefix are composed of lowercase English letters only
The total number of insert, search and startsWith calls shall not exceed 3 * 104
Solution 1: realize Trie
class Trie {
private:
bool isEnd;
Trie* next[26];
public:
Trie() {
isEnd = false;
memset(next,0,sizeof(next));
}
void insert(string word) {
Trie* node = this;
for(auto& w:word){
if(node->next[w-'a'] == nullptr){
node->next[w-'a'] = new Trie();
}
node = node->next[w-'a'];
}
node->isEnd = true;
}
bool search(string word) {
Trie* node = this;
for(auto& w:word){
node = node->next[w-'a'];
if(node == nullptr){
return false;
}
}
return node->isEnd;
}
bool startsWith(string prefix) {
Trie* node = this;
for(auto& w:prefix){
node = node->next[w-'a'];
if(node == nullptr) return false;
}
return true;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/
472. Connectives
Force buckle link
Give you a string array words without repeated words. Please find and return all conjunctions in words.
A conjunction is defined as a string consisting entirely of at least two shorter words in a given array.
Example 1:
Input: words = ["cat", "cats", "catsdogcats", "dog", "dogcatsdog", "hippopotamuses", "rat", "ratcatdogcat"]
Output: ["catsdogcats", "dogcatsdog", "ratcatdogcat"]
Explanation: "catsdogcats" consists of "cats", "dog" and "cats";
"dogcatsdog" consists of "dog", "cats" and "dog";
"ratcatdogcat" consists of "rat", "cat", "dog" and "cat".
Example 2:
Input: words = ["cat", "dog", "catdog"]
Output: ["catdog"]
Tips:
1 <= words.length <= 104
0 <= words[i].length <= 1000
words[i] consists of lowercase letters only
0 <= sum(words[i].length) <= 105
Solution 1: dictionary tree + DFS
Idea:
1. Sort words by length; Long words must be made up of short words
2. Build a prefix tree for all previous words. Students who don't know can refer to oi wiki
3. The search process is to traverse each position of the word in the prefix tree; Every time you encounter the end node in the prefix tree, you can consider trying to re match from the root node of the prefix tree from the next position of the target word, which means that s = [try: remain], and a previous conjunction try is found in S; Of course, we should also consider continuing to match on the tree.
code:
struct Trie{
bool isEnd;
vector<Trie*> next;
Trie(){
this->isEnd = false;
this->next = vector<Trie*>(26,nullptr);
}
};
class Solution {
public:
Trie* trie = new Trie();
vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {
vector<string> result;
sort(words.begin(),words.end(),[&](const string& a, const string& b){
return a.size() < b.size();
});
for(int i = 0;i<words.size();i++){
string word = words[i];
if(word.size() == 0) continue;
if(dfs(word,0)) result.emplace_back(word);
else insert(word);
}
return result;
}
bool dfs(const string& word, int start){
//Termination conditions
if(word.size() == start) return true;
Trie* node = trie;
for(int i = start;i<word.size();i++){
node = node->next[word[i]-'a'];
if(node == nullptr) return false;
if(node->isEnd){
if(dfs(word,i+1)) return true;
}
}
return false;
}
void insert(const string& word){
Trie* node = trie;
for(auto& w:word){
if(node->next[w-'a'] == nullptr){
node->next[w-'a'] = new Trie();
}
node = node->next[w-'a'];
}
node->isEnd = true;
}
};

820. Compression coding of words
Force buckle link
The effective encoding of word array words is composed of any mnemonic string s and subscript array indices, and meets the following requirements:
words.length == indices.length
Mnemonic string s ends with '#' character
For each subscript indices[i], a substring of s from indices[i] to the end of the next '#' character (but excluding '#') is exactly equal to words[i]
Give you a word array words and return the length of the minimum mnemonic string s that successfully encodes words.
Example 1:
Input: words = ["time", "me", "bell"]
Output: 10
Explanation: a set of valid codes are s = "time#bell#" and indices = [0, 2, 5].
words[0] = "time", s is a substring starting from indices[0] = 0 to the end of the next '#', as shown in the bold part, "time#bell#"
words[1] = "me", s is a substring from indices[1] = 2 to the end of the next '#', as shown in the bold part, "time#bell#"
words[2] = "bell", s is a substring from indices[2] = 5 to the end of the next '#', as shown in the bold part, "time#bell#"
Example 2:
Input: words = ["t"]
Output: 2
Explanation: a set of valid codes are s = "t#" and indices = [0].
Tips:
1 <= words.length <= 2000
1 <= words[i].length <= 7
words[i] consists of lowercase letters only
Solution 1: dictionary tree
Idea:
(1) If the word x is the suffix of Y, the word X does not need to be considered, because when encoding y, X is encoded at the same time. For example, if there are both "me" and "time" in words, we can ignore "me" without changing the answer.
If the word Y does not appear in the suffix of any other word X, then Y must be part of the encoding string.
Therefore, the goal is to retain all words that are not suffixes of other words. The final result is the sum of the length of these words plus one, because each word needs to be followed by a # symbol after coding.
(2) To find out whether different words have the same suffix, we can insert them into the dictionary tree in reverse order. For example, we have "time" and "me", and we can insert "emit" and "em" into the dictionary tree.
code:
struct Trie{
bool isEnd;
vector<Trie*> next;
Trie(){
this->isEnd = false;
this->next = vector<Trie*>(26,nullptr);
}
};
class Solution {
public:
Trie* trie = new Trie();
int minimumLengthEncoding(vector<string>& words) {
sort(words.begin(),words.end(),[&](const string& a, const string& b){
return a.size() > b.size();
});
int len = 0;
for(auto& word:words){
len += insert(word);
}
return len;
}
int insert(string& word){
Trie* node = trie;
bool isNew = false;
for(int i = word.size()-1;i>=0;i--){
if(node->next[word[i]-'a'] == nullptr){
isNew = true;//It's a new word
node->next[word[i]-'a'] = new Trie();
}
node = node->next[word[i]-'a'];
}
return isNew ? word.size()+1 : 0 ;
}
};