This blog mainly explains the calculation and algorithm implementation of massive data processing, and understands the steps that can be taken by massive data processing methods Summary of massive data processing methods , understanding data processing problems can be moved step by step Summary of massive data processing problems

Method review

1. Divide and conquer / Hash mapping + Hash statistics + heap / fast / merge sort
2. Double barrel Division
3. BitMap / Bloom Filter
4. Trie tree / database index / inverted index
5. External sorting
6. Hadoop / Mapreduce for distributed processing

Massive data computing

Calculation capacity

Before solving the problem, we should first calculate how much capacity massive data needs to occupy. Common unit conversions are as follows:

• 1 byte = 8 bit
• 1 KB = 2 10 2^{10} 210 byte = 1024 byte ≈ 1 0 3 10^3 103 byte
• 1 MB = 2 20 2^{20} 220 byte ≈ 1 0 6 10^6 106 byte
• 1 GB = 2 30 2^{30} 230 byte ≈ 1 0 9 10^9 109 byte
• 100 million= 1 0 8 10^8 108
• One integer accounts for 4 bytes, and 100 million integers account for 4 bytes* 1 0 8 10^8 108 byte ≈ 400 MB.

split

Massive data can be split into multiple machines and multiple files:

• If the amount of data is too large to be placed on one machine, split the data into multiple machines. In this way, multiple machines can cooperate together, which makes the solution of the problem faster. However, it will also lead to more complex system, and system failure and other problems need to be considered;
• If a large file cannot be directly loaded into memory when the program is running, the large file will be divided into small files, and each small file will be solved separately.

There are the following strategies for splitting:

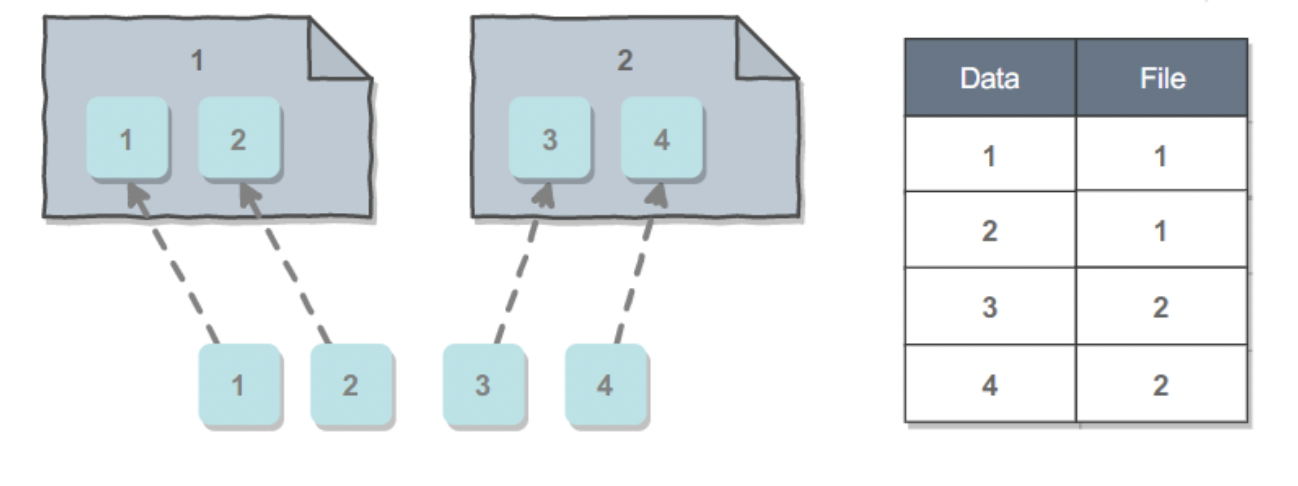
• Split according to the order of occurrence: when new data arrives, put it into the current machine first, fill it up, and then put the data on the new machine. The advantage of this method is to make full use of the resources of the system, because each machine will be filled as much as possible. The disadvantage is that a lookup table is needed to save the mapping of data to the machine. The lookup table can be very complex and very large.
  
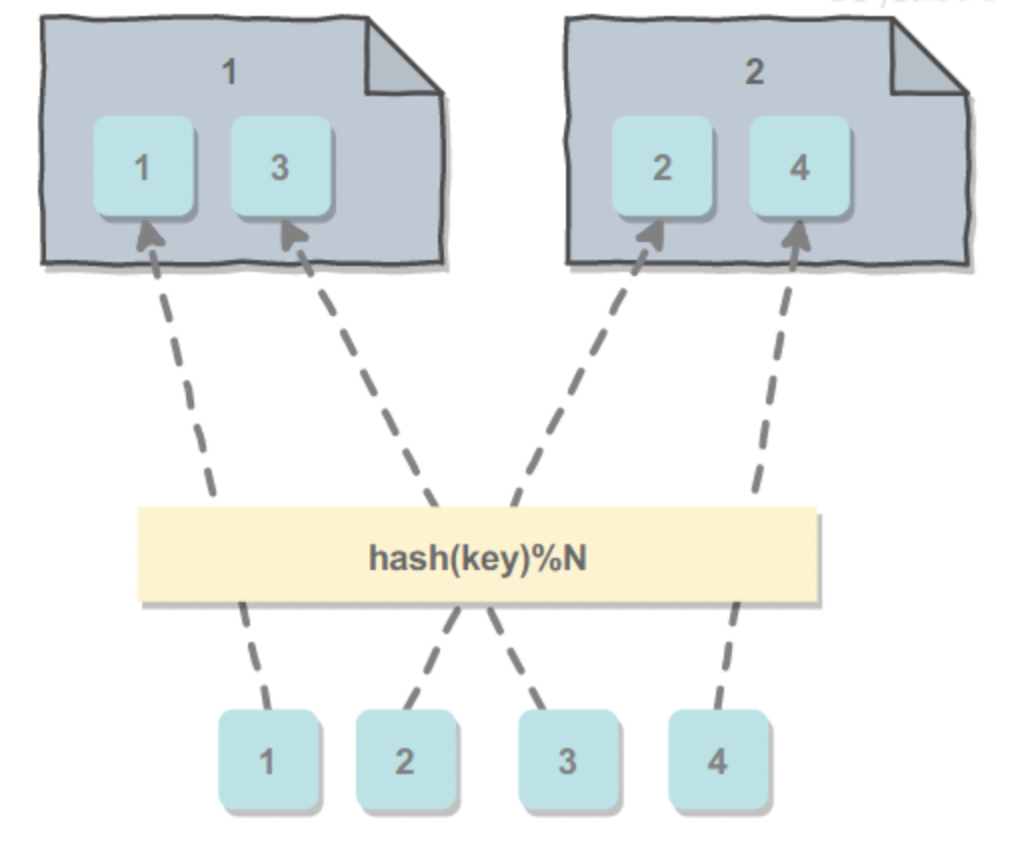
• Split by hash value: select the primary key of the data, and then obtain the machine number to which the data should be split through hash modulo hash(key)%N, where n is the number of machines. The advantage is that there is no need to use a lookup table. The disadvantage is that it may cause a machine to store too much data, or even exceed its maximum capacity.
  
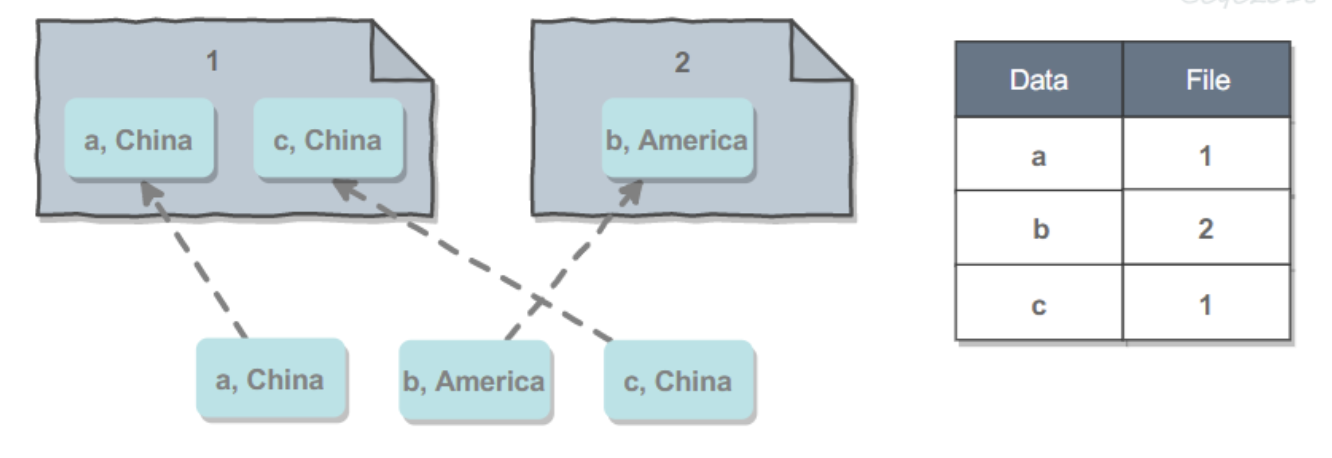
• Split according to the actual meaning of data: for example, in a social networking site system, users from the same region are more likely to become friends. If users from the same region are stored on the same machine as much as possible, when searching for a user's friend information, you can avoid searching on multiple machines, so as to reduce the delay. The disadvantage is that you also need to use a lookup table.
  

integration

The split result is only a local result, which needs to be summarized into an overall result.

Note: most massive data can be processed by hash modulus, because the same value will be assigned to the same location after hash modulus. If the memory is really small, the value of N can be larger. Moreover, Hadoop and spark are also solutions for processing massive data, but there should be no requirements for non big data.

Algorithm implementation

HashSet

Considering that the data is massive, split the data into multiple machines, and use HashSet storage on each machine. We need to split the same data to the same machine, which can be implemented by hash modulo splitting.

BitSet

If the massive data is an integer and the range is small, BitSet can be used for storage. By constructing a bit array of a certain size and mapping each integer to the bit array, it is easy to know whether an integer already exists. Because the bit array is much smaller than the integer array, a single machine can usually process a large amount of data.

class BitSet {
    int[] bitset;
    
    public BitSet(int size) {
        bitset = new int[(size >> 5) + 1]; // divide by 32
    }
    
    boolean get(int pos) {
        int wordNumber = (pos >> 5); // divide by 32
        int bitNumber = (pos & 0x1F); // mod 32
        return (bitset[wordNumber] & (1 << bitNumber)) != 0;
    }
    
    void set(int pos) {
        int wordNumber = (pos >> 5); // divide by 32
        int bitNumber = (pos & 0x1F); // mod 32
        bitset[wordNumber] |= 1 << bitNumber;
    }
 }

Bloom filter

• Bloom filter can solve the problem of mass data duplication with minimal space overhead, but it will have a certain probability of misjudgment. It is mainly used in Web blacklist system, spam filtering system and crawler website duplicate judgment system.
• The bloom filter also uses BitSet to store data, but it has been improved to remove the limitation that BitSet requires a small range of data. During storage, it requires the data to obtain K positions through k hash functions, and set the corresponding position in the BitSet to 1. When searching, you also need to get k locations through k hash functions. If all locations are 1, it indicates that the data exists.
• Due to the characteristics of hash function, the values of two different numbers obtained by hash function may be the same. If both numbers get the same value through k hash functions, the bloom filter will judge the two numbers as the same.
• It can be known that making both k and m larger will reduce the false positive rate, but it will bring higher time and space overhead.
• Bloom filter will misjudge, that is, judge a non-existent number as existing, which will cause some problems. For example, in the spam filtering system, an email will be misjudged as spam, so the email will not be received. A white list can be used for remediation.

public class BloomFilter {
    //Your bloom filter capacity
    private static final int DEFAULT_SIZE = 2 << 28;
    //bit array to store key
    private static BitSet bitSet = new BitSet(DEFAULT_SIZE);
    //The following hash function will be used to generate different hash values, which can be set at will. Don't ask me why there are so many 8, but it's lucky
    private static final int[] ints = {1, 6, 16, 38, 58, 68};

    //add method, calculate the hash value of the key, and set the corresponding subscript to true
    public void add(Object key) {
        Arrays.stream(ints).forEach(i -> bitSet.set(hash(key, i)));
    }

    //Judge whether the key exists. true does not necessarily mean that the key exists, but false does not
    public boolean isContain(Object key) {
         boolean result = true;
        for (int i : ints) {
        	//If there is a short circuit and a bit is false, false will be returned
            result = result && bitSet.get(hash(key, i));
        }
        return result;
    }

    //The hash function draws lessons from the hashmap perturbation algorithm. It is strongly recommended that you understand the hash algorithm. This design is really cow leather and lightning
    private int hash(Object key, int i) {
        int h;
        return key == null ? 0 : (i * (DEFAULT_SIZE - 1) & ((h = key.hashCode()) ^ (h >>> 16)));
    }
}

Prefix tree (Trie)

Dictionary tree, also known as word lookup tree or key tree, is a tree structure and a variant of hash tree. The typical application is to count and sort a large number of strings (but not limited to strings), so it is often used by search engine system for text word frequency statistics. It has the advantages of minimizing unnecessary string comparison and higher query efficiency than hash table.

Trie's core idea is space for time. The common prefix of string is used to reduce the overhead of query time in order to improve efficiency.

Three basic properties:

• The root node does not contain characters. Except for the root node, each node contains only one character.
• From the root node to a node, the characters passing through the path are connected to the corresponding string of the node.
• All child nodes of each node contain different characters.

class Trie {
    private class Node {
        Node[] childs = new Node[26];
        boolean isLeaf;
    }
    
    private Node root = new Node();
    
    public Trie() {
    }
    
    public void insert(String word) {
        insert(word, root);
    }
    
    private void insert(String word, Node node) {
        if (node == null) return;
        if (word.length() == 0) {
            node.isLeaf = true;
            return;
        }
        int index = indexForChar(word.charAt(0));
        if (node.childs[index] == null) {
            node.childs[index] = new Node();
        }
        insert(word.substring(1), node.childs[index]);
    }
    
    public boolean search(String word) {
        return search(word, root);
    }
    
    private boolean search(String word, Node node) {
        if (node == null) return false;
        if (word.length() == 0) return node.isLeaf;
        int index = indexForChar(word.charAt(0));
        return search(word.substring(1), node.childs[index]);
    }
    
    public boolean startsWith(String prefix) {
        return startWith(prefix, root);
    }
    
    private boolean startWith(String prefix, Node node) {
        if (node == null) return false;
        if (prefix.length() == 0) return true;
        int index = indexForChar(prefix.charAt(0));
        return startWith(prefix.substring(1), node.childs[index]);
    }
    
    private int indexForChar(char c) {
        return c - 'a';
    }
}