Examples
LeetCode 239. Sliding Window Maximum
There may be no way to register, just Click here
subject
Give you an integer array nums, with a sliding window of \ (k \) moving from the leftmost side of the array to the rightmost side of the array. You can only see \ (k \) numbers in the sliding window. The sliding window moves only one bit to the right at a time.
Returns the maximum value in the sliding window.
Brief analysis
This problem can't be solved by violence (time complexity \ (O(nk) \)). At this time, we need
Humdrum Queue
To understand monotone queue, you need to know what monotone is.
The definition of monotonicity of function here is similar to that here.
The monotonicity of a function can also be called the increase or decrease of a function. When the independent variable of function f(x) increases (or decreases) in its definition interval, and the function value f(x) also increases (or decreases), the function is said to have monotonicity in this interval.
The same is true for monotonic queues, which can be regarded as a subset of queues, satisfying \ (\ forall I (1 \ le I \ LT size) \ text {} queue [i] \ Le queue [i + 1] \) or \ (\ forall I (1 \ le I \ LT size) \ text {} queue [i] \ Ge queue [i + 1] \).
realization
These functions need to be realized:
struct HumdrumQueue{
void pop(int val){
}
void push(int val){
}
int front(){
return 0;
}
int size(){
return 0;
}
};
Bottom container
Since monotone queue is a variant of queue and STL queue is based on deque, I chose deque privately.
Complete code (I also added a back()):
struct HumdrumQueue {
deque<int> q;
void pop(int val) {
if (!this->q.empty() && this->q.front() == val) {
this->q.pop_front();
}
}
void push(int val) {
while (!this->q.empty() && val > this->q.back()) {
this->q.pop_back();
}
this->q.push_back(val);
}
int front() {
return this->q.front();
}
int back() {
return this->q.back();
}
int size() {
return this->q.size();
}
};
Among them, the pop function needs to judge that the number of team leaders is the same as this number.
push uses the idea of leaving the team when it is big. Please think about why.
Please think about why.
Solve the sliding window problem
vector<int> maxSlidingWindow(vector<int> nums, int k) {
HumdrumQueue hq;
vector<int> answer;
for (int i = 0; i < k; i++) {
hq.push(nums[i]);
}
answer.push_back(hq.front());
for (int i = k; i < int(nums.size()); i++) {
hq.pop(nums[i - k]);
hq.push(nums[i]);
answer.push_back(hq.front());
}
return answer;
}
\(\ textbf{remove the first element, add the last element, record the maximum, Well done!!} \)
Integration, submission
LeetCode's submission method is somewhat different
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
struct HumdrumQueue {
deque<int> q;
void pop(int val) {
if (!this->q.empty() && this->q.front() == val) {
this->q.pop_front();
}
}
void push(int val) {
while (!this->q.empty() && val > this->q.back()) {
this->q.pop_back();
}
this->q.push_back(val);
}
int front() {
return this->q.front();
}
int back() {
return this->q.back();
}
int size() {
return this->q.size();
}
};
HumdrumQueue hq;
vector<int> answer;
for (int i = 0; i < k; i++) {
hq.push(nums[i]);
}
answer.push_back(hq.front());
for (int i = k; i < int(nums.size()); i++) {
hq.pop(nums[i - k]);
hq.push(nums[i]);
answer.push_back(hq.front());
}
return answer;
}
};
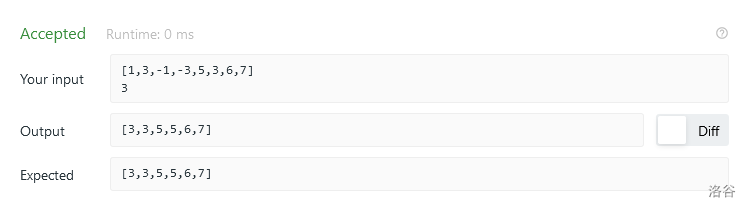
The time complexity and space complexity are \ (O(n) \), which can be solved perfectly.
Other topics
P1886 sliding window / [template] monotonic queue
subject
There is a sequence \ (a \) with a length of \ (n \) and a window with a size of \ (k \). Now slide from the left to the right, one unit at a time, and find the maximum and minimum values in the window after each slide.
For example:
The array is \([1,3,-1,-3,5,3,6,7]\), and \(k = 3\).
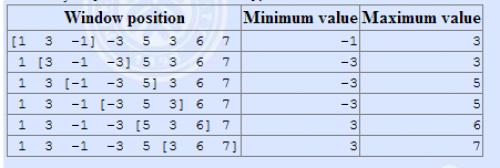
analysis
This question is similar to the original one.
Just added a minimal.
#include <bits/stdc++.h>
using namespace std;
struct HumdrumQueue {
deque<int> q;
void pop(int val) {
if (!this->q.empty() && this->q.front() == val) {
this->q.pop_front();
}
}
void push(int val) {
while (!this->q.empty() && val > this->q.back()) {
this->q.pop_back();
}
this->q.push_back(val);
}
void push2(int val) {
while (!this->q.empty() && val < this->q.back()) {
this->q.pop_back();
}
this->q.push_back(val);
}
int front() {
return this->q.front();
}
int back() {
return this->q.back();
}
int size() {
return this->q.size();
}
};
vector<int> maxSlidingWindow(vector<int> nums, int k) {
HumdrumQueue hq;
vector<int> answer;
for (int i = 0; i < k; i++) {
hq.push(nums[i]);
}
answer.push_back(hq.front());
for (int i = k; i < int(nums.size()); i++) {
hq.pop(nums[i - k]);
hq.push(nums[i]);
answer.push_back(hq.front());
}
return answer;
}
vector<int> minSlidingWindow(vector<int> nums, int k) {
HumdrumQueue hq;
vector<int> answer;
for (int i = 0; i < k; i++) {
hq.push2(nums[i]);
}
answer.push_back(hq.front());
for (int i = k; i < int(nums.size()); i++) {
hq.pop(nums[i - k]);
hq.push2(nums[i]);
answer.push_back(hq.front());
}
return answer;
}
int main() {
int n, k;
cin >> n >> k;
vector<int> v;
for (int i = 0; i < n; i++) {
int a;
cin >> a;
v.push_back(a);
}
vector<int> result = maxSlidingWindow(v, k);
vector<int> result2 = minSlidingWindow(v, k);
for (int i = 0; i < result2.size(); i++) {
cout << result2[i] << ' ';
}
cout << '\n';
for (int i = 0; i < result.size(); i++) {
cout << result[i] << ' ';
}
return 0;
}
Other recommended topics
I used another approach:
#include <bits/stdc++.h>
using namespace std;
int a[1000005];
int main(){
int t,n;
cin>>t;
while(t--){
cin>>n;
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
set<int> s;
int left=0,right=0,answer=0;
while(right<n){
while(right<n&&!s.count(a[right])){
s.insert(a[right++]);
}
answer = max(answer,right-left);
s.erase(a[left++]);
}
printf("%d\n",answer);
}
return 0;
}
Sliding window / monotone queue template code
struct HumdrumQueue {
deque<int> q;
void pop(int val) {
if (!this->q.empty() && this->q.front() == val) {
this->q.pop_front();
}
}
void push(int val) {
while (!this->q.empty() && val > this->q.back()) {
this->q.pop_back();
}
this->q.push_back(val);
}
void push2(int val) {
while (!this->q.empty() && val < this->q.back()) {
this->q.pop_back();
}
this->q.push_back(val);
}
int front() {
return this->q.front();
}
int back() {
return this->q.back();
}
int size() {
return this->q.size();
}
};
vector<int> maxSlidingWindow(vector<int> nums, int k) {
HumdrumQueue hq;
vector<int> answer;
for (int i = 0; i < k; i++) {
hq.push(nums[i]);
}
answer.push_back(hq.front());
for (int i = k; i < int(nums.size()); i++) {
hq.pop(nums[i - k]);
hq.push(nums[i]);
answer.push_back(hq.front());
}
return answer;
}
vector<int> minSlidingWindow(vector<int> nums, int k) {
HumdrumQueue hq;
vector<int> answer;
for (int i = 0; i < k; i++) {
hq.push2(nums[i]);
}
answer.push_back(hq.front());
for (int i = k; i < int(nums.size()); i++) {
hq.pop(nums[i - k]);
hq.push2(nums[i]);
answer.push_back(hq.front());
}
return answer;
}
Where humdrumqueue Push is large, humdrumqueue Push2 is small.