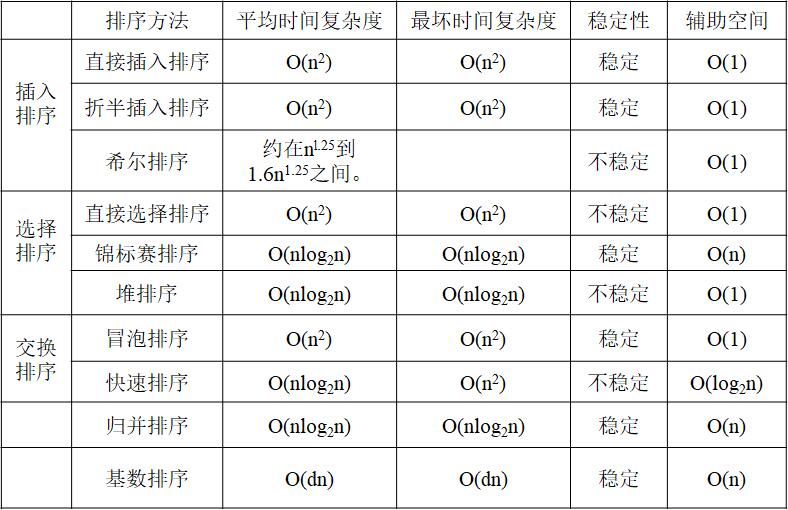
Summary of ranking methods (stability and complexity issues)
preface
Data structure final exam, to analyze various sorting methods, complexity problems and stability problems, let's summarize here. I hope it can help you who are reading this article! ( ^ - ^ )!
stability
Generally speaking, the so-called stability is that if there are two equal numbers in an array, arr[i]=arr[j], I < J, and there is still I < J after sorting. That is, if two equal numbers are not exchanged, this sort is called stable.
Time complexity
The so-called time complexity is the time used by the whole algorithm program, which is usually calculated according to the cycle.
1, Direct insertion sort
Idea analysis: (according to the name of the sorting method, this is a very violent method.) in essence, it is to traverse backward from the second number on the basis of the original array (here we use the comparison between the later and the previous to prevent the subscript from crossing the boundary, we will traverse from the second bit). If we encounter the latter number (recorded as temp=arr[i]) If it is less than the previous number arr[i-1], start looking forward until it is not less than temp. And each time you look forward, move the number back one bit, and finally insert the current number into the position it should be. In essence, I the front can be regarded as an ordered part, and the back can be regarded as an unordered part.
Maybe a little dizzy. Let's look at the analysis chart > <!

Then analyze the code:
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
//Direct insert sort
void Directinsertionsort(int a[],int length)
{
int i, j;
for (i = 1; i < length; i++){
int temp = a[i];
for (j = i; (j > 0) && (a[j - 1] > temp); j--)//Border issues, j also can not cross the border!
{
a[j] = a[j - 1];
}
a[j] = temp;
}
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n;i++)
cin >> arr[i];
Directinsertionsort(arr, n);
for (int i = 0; i < n;i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
Stability: stable; Time complexity: O(n2)
2, Sort by half insertion
Train of thought analysis: dichotomy, without too much explanation. (for each comparison from the middle of the previous sequence of i, gradually narrow the range until the position that should be inserted is found. Finally, move all the numbers from the insertion position to i backward, and finally insert the numbers.)
See Figure Analysis:

Analysis code:
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
//Sort by half insertion
void Splitinsertionsort(int a[],int length)
{
for (int i = 1; i < length;i++){
int temp = a[i];
int left = 0, right = i - 1;
while(left<=right){//Binary classic template (still orderly in front and disordered behind)
int mid = (left + right) / 2;
if(temp<a[mid])
right = mid - 1;
else
left = mid + 1;
}
for (int k = i - 1; k >= left;k--)
a[k + 1] = a[k];
a[left] = temp;
}
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n;i++)
cin >> arr[i];
Splitinsertionsort(arr, n);
for (int i = 0; i < n;i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
Stability: stable; Complexity: O(n2)
3, Hill sort
Idea analysis: from the beginning, divide the numbers in the array into several groups. Those with the same spacing in one group usually set the distance to half the length of the original array. eg. if the spacing is 4, the data 1, 5, 9... Are a group, 2, 6, 10... Are a group, 3, 7, 11... Are a group, and 4, 8, 12... Are a group. Then perform the direct insertion sort within the group. After the first execution, reduce the spacing by half and operate again. Cycle this step until the spacing is 1. The entire array becomes a group. After the direct insertion sort is completed, the final required array is obtained.
To analyze the code:
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
//Shell Sort
void Shellsort(int a[], int length)
{
int gap = length / 2;//Initial spacing
while (gap)
{
for (int start = gap; start < 2 * gap && start < length; start++)
{
for (int i = start; i < length; i += gap)//Direct insertion sort within group
{
int temp = a[i];
int j = i;
while (j >= gap && temp < a[j - gap])
{
a[j] = a[j - gap];
j -= gap;
}
a[j] = temp;
}
}
gap /= 2;//Reduce spacing each time
}
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n; i++)
cin >> arr[i];
Shellsort(arr, n);
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
Stability: unstable; The time complexity is O(n1.25~1.6n1.25)
4, Select sort
For details, see Simple sort
Note: the code over there is ugly. See the code below
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
void Selectionsort(int a[],int length)
{
for (int i = 0; i < length;i++)
for (int j = i + 1; j < length;i++){
if(a[i]>a[j]){
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n; i++)
cin >> arr[i];
Selectionsort(arr, n);
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
Stability: unstable; Time complexity: O (n2)
5, Tournament ranking
Train of thought analysis: compare two groups of teams according to the way of competition, and find the smallest one each time until the end of the competition.
#include <iostream>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int temp[N];
template <class T>
struct DataNode
{
T data;
int index;
int flag;
};
int PowerOfTwo(int n)
{
int k = 2;
while(k<n)
k = 2 * k;
return k;
}
template<class T>
bool operator<(const DataNode<T>&x,const DataNode<T>&y)
{
return (x.data < y.data);
}
template<class T>
void UpdateTree(DataNode<T>* tree,int i)
{
tree[(i - 1) / 2] = (i % 2 == 0 ? tree[i - 1] : tree[i + 1]);
i = (i - 1) / 2;
while(i>0){
int j = (i % 2 == 0 ? i - 1 : i + 1);
if (tree[i].flag == 0)
tree[(i - 1) / 2] = tree[j];
else if(tree[j].flag==0)
tree[(i - 1) / 2] = tree[i];
else if(tree[i]<tree[j])
tree[(i - 1) / 2] = tree[i];
else
tree[(i - 1) / 2] = tree[j];
i = (i - 1) / 2;
}
}
template<class T>
void Tournament(T* pa,int n)
{
DataNode<T> item;
int bottomsize = PowerOfTwo(n);
int treesize = 2 * bottomsize - 1;
DataNode<T> *tree = new DataNode<T>[treesize];
int i,j;
for (j = bottomsize - 1, i = 0; j < treesize;j++,i++){
item.index = j;
if(i<n){
item.data = pa[i];
item.flag = 1;
}
else{
item.data = T();
item.flag = 0;
}
tree[j] = item;
}
i = bottomsize - 1;
while(i>0){
j = i;
while(j<2*i){
if(tree[j+1].flag==0||tree[j].data<tree[j+1].data)
tree[(j - 1) / 2] = tree[j];
else
tree[(j - 1) / 2] = tree[j + 1];
j = j + 2;
}
i = (i - 1) / 2;
}
for (i = 0; i < n - 1;i++){
pa[i] = tree[0].data;
tree[tree[0].index].flag = 0;
UpdateTree(tree, tree[0].index);
}
pa[n - 1] = tree[0].data;
delete[] tree;
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n; i++)
cin >> arr[i];
Tournament(arr, n);
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
6, Heap sort
Train of thought analysis: sort by stacking
#include <iostream>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int temp[N];
template <class T>
void PercolateDown(T *pa, int pos, int size)
{
int p = pos, c = 2 * p + 1;
T temp = pa[p];
while (c < size)
{
if (c + 1 < size && pa[c + 1] > pa[c])
++c;
if (temp >= pa[c])
break;
else
{
pa[p] = pa[c];
p = c;
c = 2 * p + 1;
}
}
pa[p] = temp;
}
//Build pile
template <class T>
void BuildHeap(T *pa, int size)
{
for (int i = size / 2 - 1; i >= 0; i--)
PercolateDown(pa, i, size);
}
//Heap sort
template<class T>
void HeapSort(T* pa,int n)
{
T temp;
BuildHeap(pa, n);
for (int i = n - 1; i > 0; i--){
temp = pa[0];
pa[0] = pa[i];
pa[i] = temp;
PercolateDown(pa, 0, i);
}
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n; i++)
cin >> arr[i];
HeapSort(arr, n);
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
7, Bubble sorting
For details, see Simple sort
Note: the code over there is ugly. See the code below
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
void Bubblesort(int a[], int length)
{
int i,j = length;
while (j >= 0)
{
for (i = 0; i + 1 < j; i++)
{
if (a[i] > a[i + 1])
{
int temp = a[i];
a[i] = a[i + 1];
a[i + 1] = temp;
}
}
i = 0;
j--;
}
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n; i++)
cin >> arr[i];
Bubblesort(arr, n);
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
8, Quick sort
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
void Quicksort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i ++ ; while (q[i] < x);
do j -- ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
Quicksort(q, l, j), Quicksort(q, j + 1, r);
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n; i++)
cin >> arr[i];
Quicksort(arr, 0, n - 1);
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
9, Merge sort
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int temp[N];
//Merge sort
void Mergesort(int a[], int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
Mergesort(a, l, mid);
Mergesort(a, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (a[i] <= a[j]) temp[k ++ ] = a[i ++ ];
else temp[k ++ ] = a[j ++ ];
while (i <= mid) temp[k ++ ] = a[i ++ ];
while (j <= r) temp[k ++ ] = a[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) a[i] = temp[j];
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n; i++)
cin >> arr[i];
Mergesort(arr, 0, n - 1);
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
10, Cardinality sort
#include <iostream>
#include<queue>
using namespace std;
const int N = 1e5 + 10;
//Cardinality sort
void Radixsort(int a[], int length)
{
queue<int> Q[10];
int base = 1, flag = 1, k, i;
while(flag)
{
for (i = 0; i < length;i++){
k = (a[i] / base) % 10;
Q[k].push(a[i]);
}
base *= 10;
flag = 0;
i = 0;
for (k = 0; k < 10;k++)
while(!Q[k].empty()){
a[i++] = Q[k].front();
Q[k].pop();
if(a[i-1]/base!=0&&flag==0)
flag = 1;
}
}
}
int main()
{
int n;
cin >> n;
int arr[N];
for (int i = 0; i < n; i++)
cin >> arr[i];
Radixsort(arr, n);
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
Summary form: