21. Merge two sequential tables
Input: l1 = [1,2,4], l2 = [1,3,4]
Output: [1,1,2,3,4,4]
There is nothing to say about using an empty node.
class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
dummy = ListNode()
p = dummy
while l1 and l2:
if l1.val < l2.val:
dummy.next = l1
dummy = dummy.next
l1 = l1.next
else:
dummy.next = l2
dummy = dummy.next
l2 = l2.next
while l1:
dummy.next = l1
dummy = dummy.next
l1 = l1.next
while l2:
dummy.next = l2
dummy = dummy.next
l2 = l2.next
return p.next
23. Merge K ascending lists
Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
class Solution:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
import heapq
heapMin = []
for ls in lists:
while ls:
heapq.heappush(heapMin, ls.val)
ls = ls.next
dummy = ListNode(0)
p = dummy
while heapMin:
p.next = ListNode(heapq.heappop(heapMin))
p = p.next
return dummy.next
Use the minimum heap to sort all elements of all lists, and then put them into the linked list in turn.
Use of heap:
import heapq heapq.heappush(heapMin, ls.val) heapq.heappop(heapMin)
19. Delete the penultimate node of the linked list
Input: head = [1,2,3,4,5], n = 2
Output: [1,2,3,5]
Try using a single scan implementation.
You can let p1 take step k first. Now p1 only needs to take step n-k to reach the end of the linked list. At this time, p2 points to the head node and goes back. When p1 goes to the end, p2 goes to the penultimate node.
In this way, the penultimate k-th node is obtained.
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
def findFromEnd(head: ListNode, k: int):
p1 = head
while k:
p1 = p1.next
k = k - 1
p2 = head
while p1:
p2 = p2.next
p1 = p1.next
return p2
dummy = ListNode(0)
dummy.next = head
x = findFromEnd(dummy, n+1)
x.next = x.next.next
return dummy.next
However, note that we also use the technique of virtual head node to prevent the occurrence of null pointer. For example, the linked list has a total of 5 nodes. The topic asks you to delete the penultimate node, that is, the first node. According to the algorithm logic, you should first find the penultimate node. But there is no node in front of the first node, which will make an error.
141. Circular linked list 142 Circular linked list II
Whenever the slow pointer slow advances one step, the fast pointer fast advances two steps.
If fast finally encounters a null pointer, it indicates that there is no ring in the linked list; If fast finally meets slow, it must be that fast exceeds slow by one circle, indicating that the linked list contains rings.
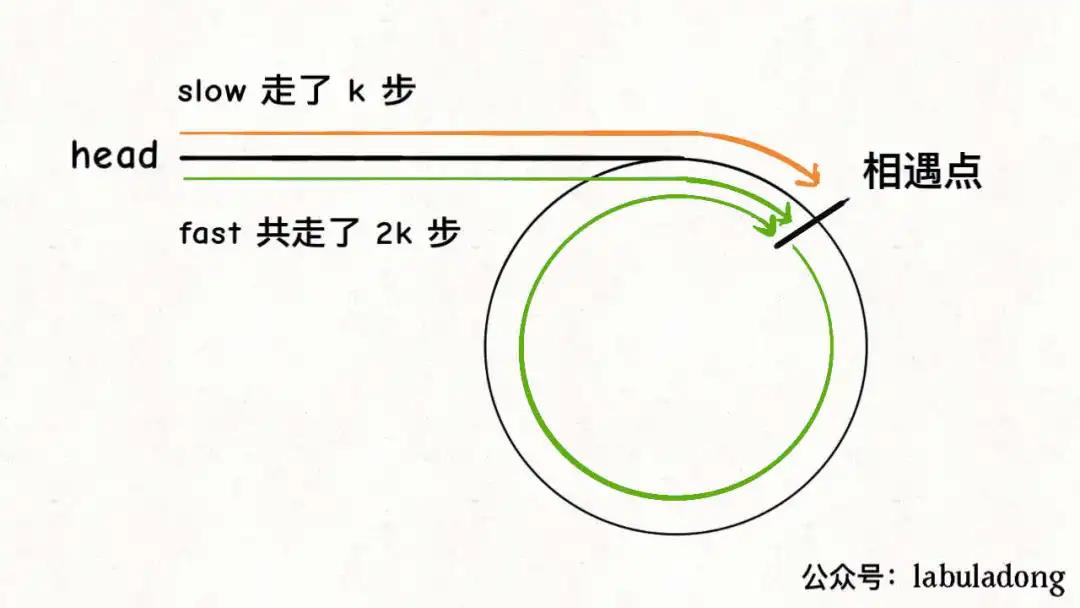
It can be seen that when the fast and slow pointers meet, let either pointer point to the head node, and then let them move forward at the same speed. The node position when they meet again is the beginning of the ring.
We assume that when the fast and slow pointers meet, the slow pointer slow takes k steps, so the fast pointer fast must take 2k steps
Fast must have taken k steps more than slow. In fact, this extra k step is that the fast pointer rotates in a circle in the ring, so the value of k is an "integer multiple" of the length of the ring.
Assuming that the distance between the meeting point and the starting point of the ring is m, combined with the slow pointer in the figure above, the distance between the starting point of the ring and the head node is k - m, that is, if you move K - M steps forward from the head, you can reach the starting point of the ring.
Coincidentally, if you continue to go k - m steps from the meeting point, you also happen to reach the starting point of the ring. Because in combination with the fast pointer in the figure above, you can go back to the meeting point by taking k steps from the meeting point. Then you must go to the starting point of the ring by taking k - m steps:
Therefore, as long as we re point any one of the fast and slow pointers to the head, and then the two pointers move forward at the same speed, we will meet after k - m steps, and the place where we meet is the starting point of the ring.
def detectCycle(self, head: ListNode) -> ListNode:
slow = head
fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
if fast == slow:
break
if fast == None or fast.next== None:
# Indicates that there is no ring
return None
# Re point to the head node
slow = head
# The speed pointer is synchronized, and the intersection point is the starting point of the ring
while slow != fast:
fast = fast.next
slow = slow.next
return slow
876. Intermediate node of linked list
Whenever the slow pointer slow advances one step, the fast pointer fast advances two steps. In this way, when fast reaches the end of the linked list, slow points to the midpoint of the linked list.
class Solution:
def middleNode(self, head: ListNode) -> ListNode:
slow = head
fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
return slow
160. Intersecting linked list
Enter the head nodes headA and headB of the two linked lists. The two linked lists may intersect.
If it intersects, your algorithm should return the intersecting node; If there is no intersection, null is returned.
Therefore, we can let p1 traverse list a and then start to traverse List B, and p2 traverse List B and then start to traverse list A. This is equivalent to "logically" connecting the two lists together.
If the splicing is carried out in this way, p1 and p2 can enter the common part at the same time, that is, reach the intersection node c1 at the same time:
Then you may ask, if there is no intersection point between the two linked lists, can null be returned correctly?
This logic can cover this situation, which is equivalent to that c1 node is a null null null pointer, which can correctly return null.
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
p1 = headA
p2 = headB
while p1!= p2:
if p1 == None:
p1 = headB
else:
p1 = p1.next
if p2 == None:
p2 = headA
else:
p2 = p2.next
return p1