This article is long. You can click the directory below to view the corresponding content.

I tree

1. Basic concepts

   tree is a nonlinear data structure, which consists of n nodes and a set with hierarchical relationship. In fact, it is a big tree growing upside down, with many leaves added to one root.
  the tree must contain a root node and several branch nodes and leaf nodes. And the children of each branch node form a subtree. The root node of each subtree has only one precursor, but it can be followed by many successors. In addition to the root node, each node has one and only one parent node.
  

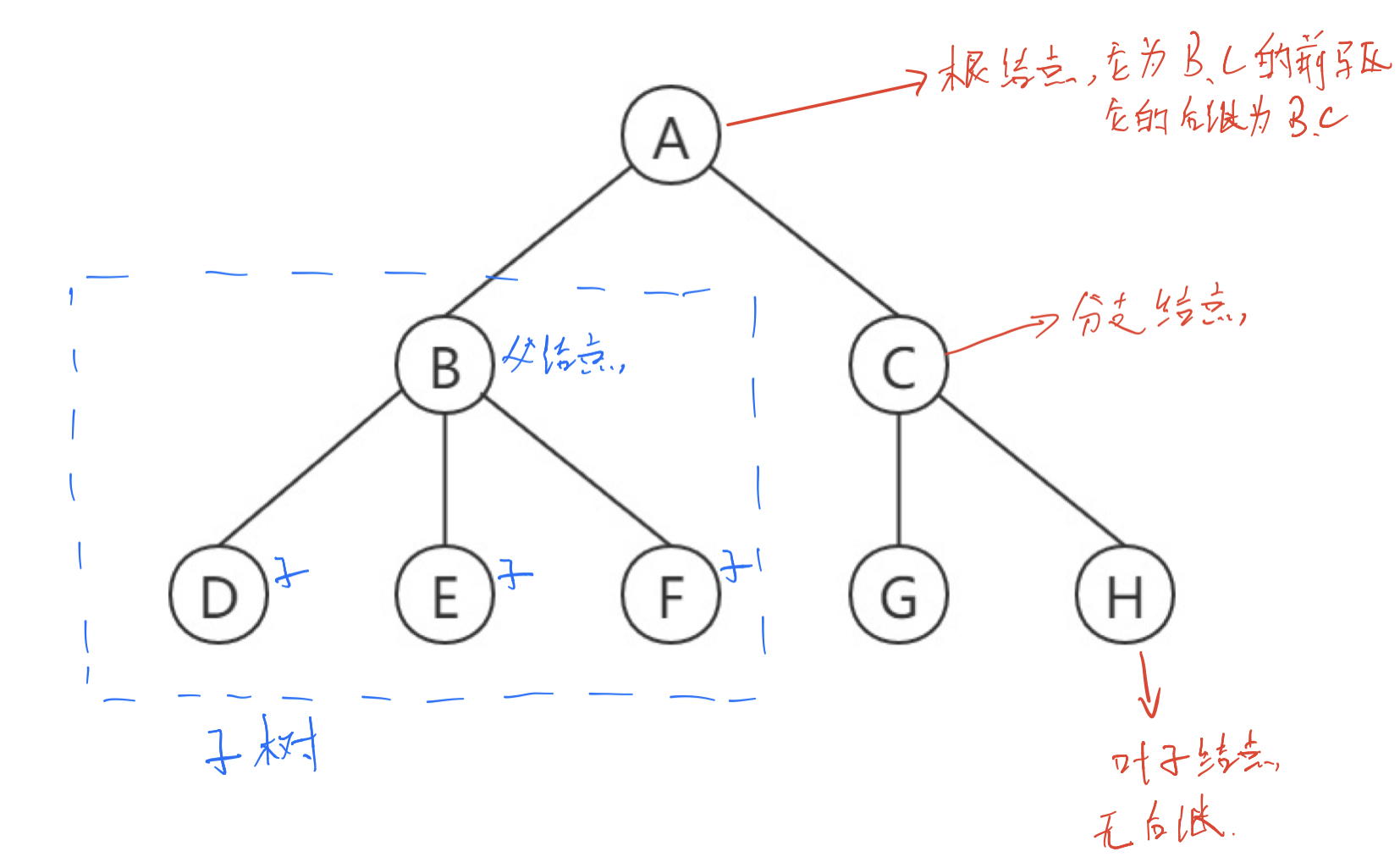
2. Basic properties of tree

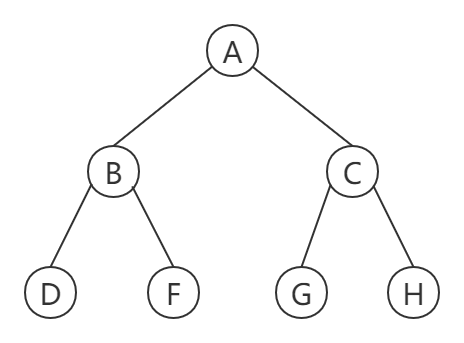
1. Node degree: the number of subtrees in A node becomes the degree of the node. In the above figure, the degree of A is 2, the degree of B is 3, and the degree of D is 0
2. Leaf node or terminal node: a node with a degree of 0 is a leaf node. D, E, F, G and H in the above figure.
3. Branch node: node whose degree is not 0. B and C in the figure above.
4. Parent node: if A node contains child nodes, it is called the parent node. In the above figure, A is the parent node of B and C, and B is the parent node of D, E and F.
5. Child node: the root node of the subtree contained in a node is called the child node of the node. In the above figure, B and C are the child nodes of A
6. Brother node: nodes with the same parent node are called brother nodes. In the figure above, B and C are brothers, and D, E and F are brothers.
7. Tree degree: the degree of the largest node in a tree. The largest node in the figure above is B 3, so 3 is the degree of the tree.
8. Node hierarchy: the hierarchy of the root node is defined as the first layer, and the child nodes of the root are defined as the second layer.
9. Height or depth of the tree: the maximum level of nodes in the tree. The height in the figure above is 3
10. Cousin node: the node whose parent node is in the same layer. In the figure above, DEFGH are cousins to each other.
11. Ancestor of node: from the root node to all nodes on the branch through which the node passes. In the figure above, A is the ancestor of all nodes
12. Forest: a collection of N disjoint trees is called forest.

3. Representation of tree

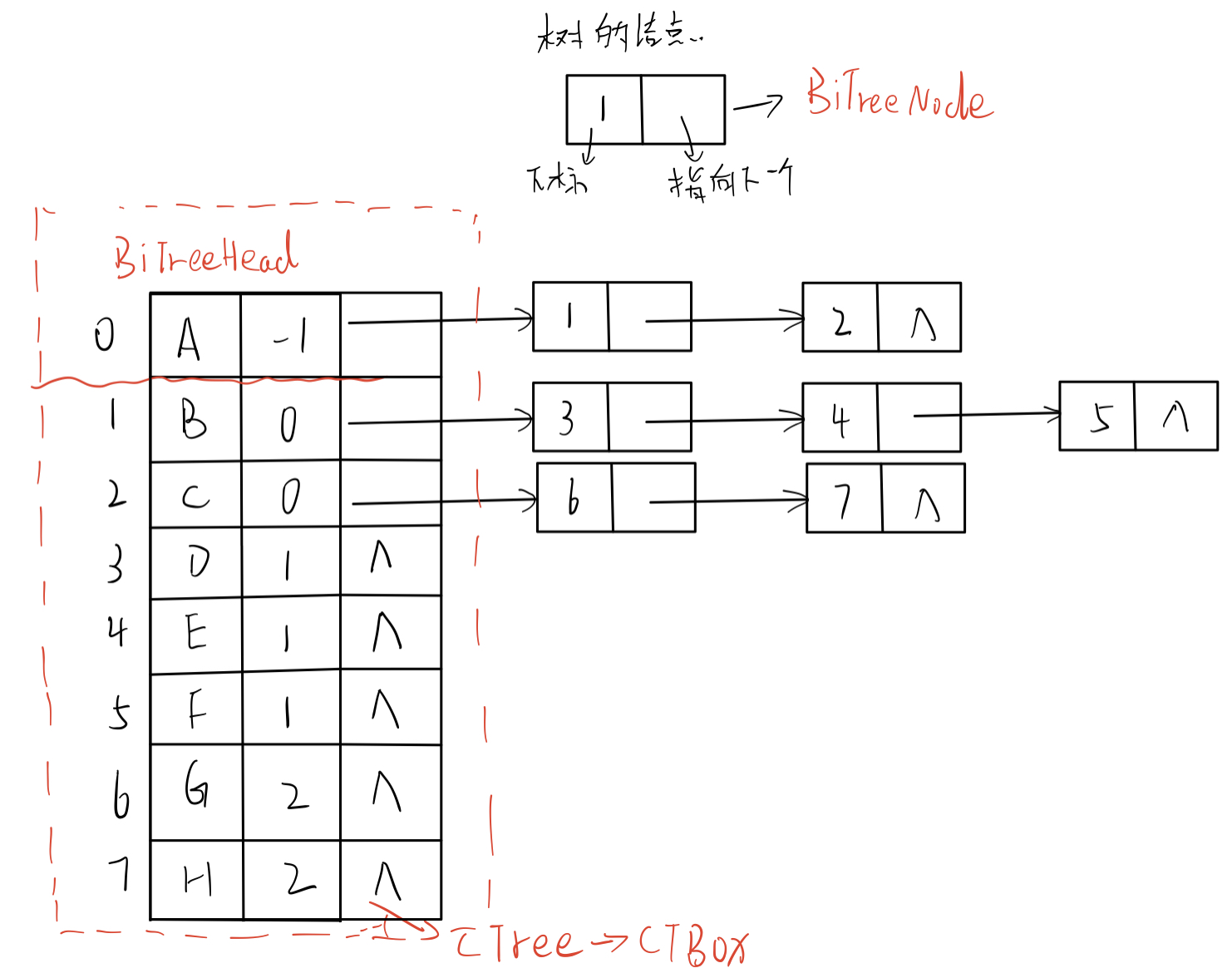
1). Child representation

1. data structure

// Child node structure
struct BiTreeNode
{
	int child; // Subscript of child node
	BiTreeNode* next;  // Pointer to the next node
}

// 
struct BiTreeHead
{
	DataType data;		// Store the data of nodes in the tree
	BiTreeNode* firstchild;  // Pointer to the first child
}

struct CTree{
    CTBox BiTreeHead[MAX_SIZE]; //Array of storage nodes
    int n,r; //Number of nodes and location of tree roots
};

1. Illustration
   
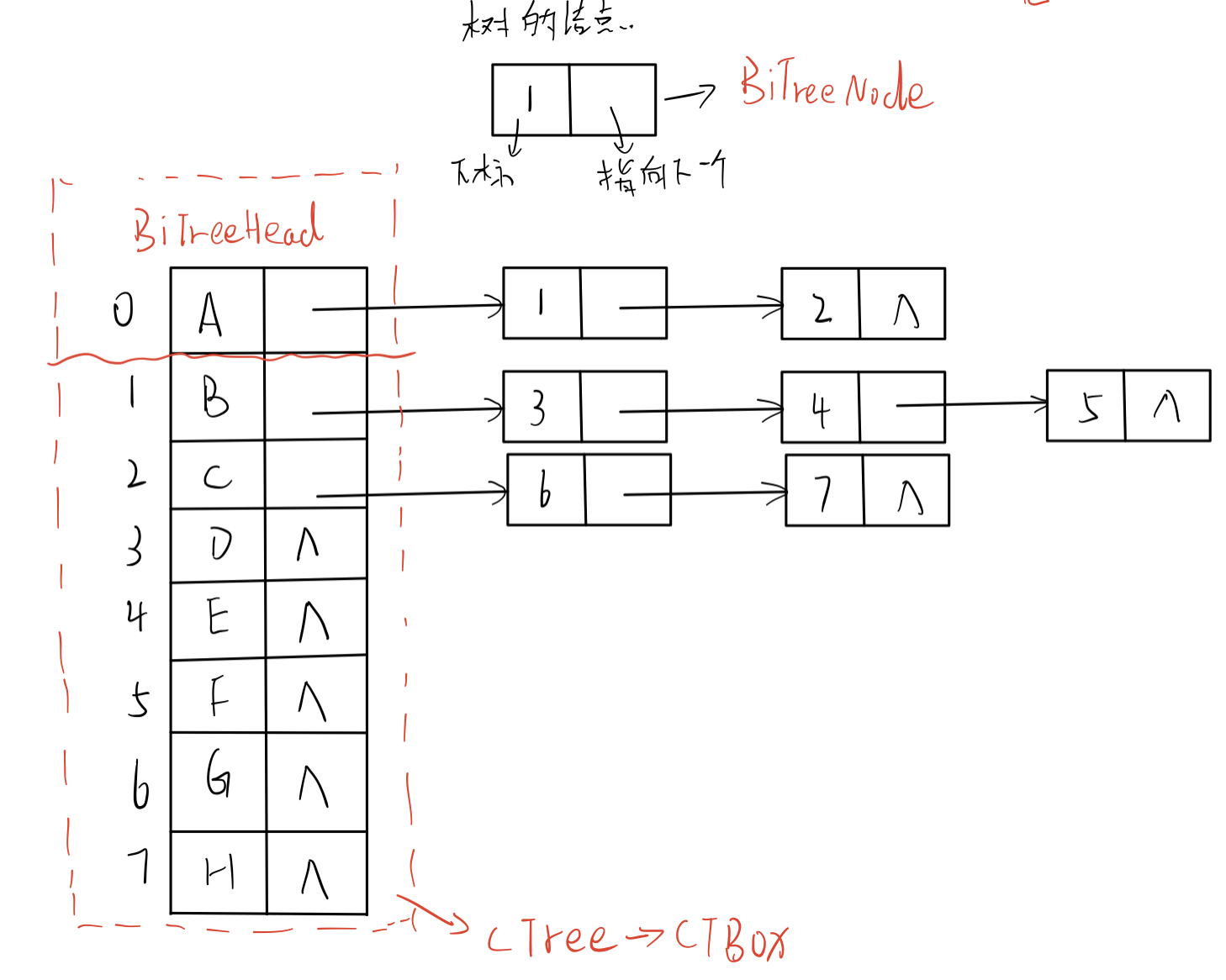
2. Advantages and disadvantages
   Advantages: it is convenient to find children. Disadvantages: it is inconvenient to find parents

2). Parental representation

1. data structure

struct PTNode{
    DataType data; //Data type of node in tree
    int parent;    //The position subscript of the parent node of the node in the array
};
struct PTree{
    PTNode tnode[MAX_SIZE]; //Store all nodes in the tree
    int n;    //Position subscript and node number of root
};

1. Illustration
   
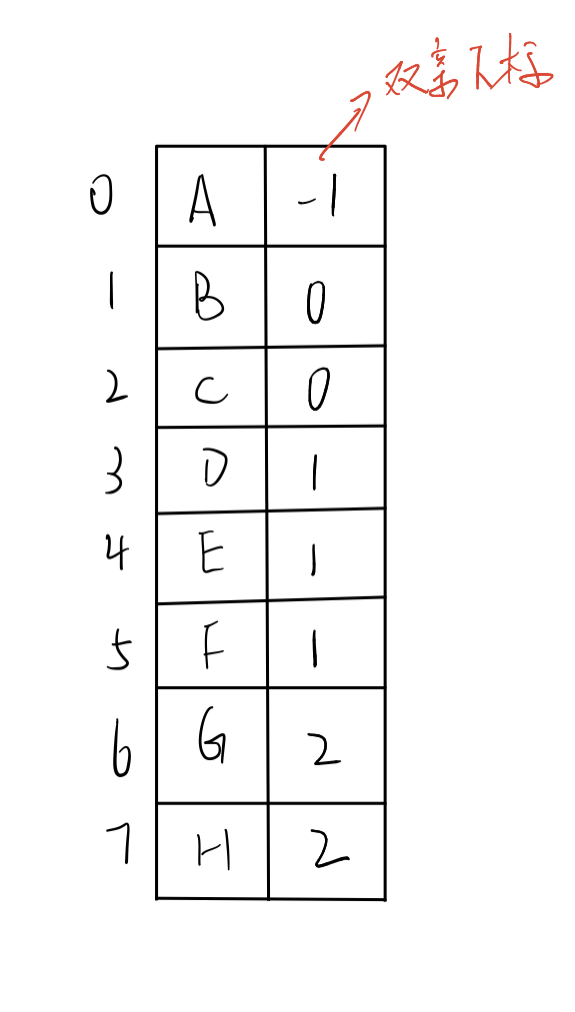
2. Advantages and disadvantages
   Advantages: it is convenient to find parents. Disadvantages: it is inconvenient to find children

3). Child parent representation

In fact, it is the integration of child representation and parent representation.

1. data structure

// Child node structure
struct BiTreeNode
{
	int child; // Subscript of child node
	BiTreeNode* next;  // Pointer to the next node
}

// 
struct BiTreeHead
{
	DataType data;		// Store the data of nodes in the tree
	BiTreeNode* firstchild;  // Pointer to the first child
	int parent; // Subscript of parents
}

struct CTree{
    CTBox BiTreeHead[MAX_SIZE]; //Array of storage nodes
    int n,r; //Number of nodes and location of tree roots
};

1. Illustration
   

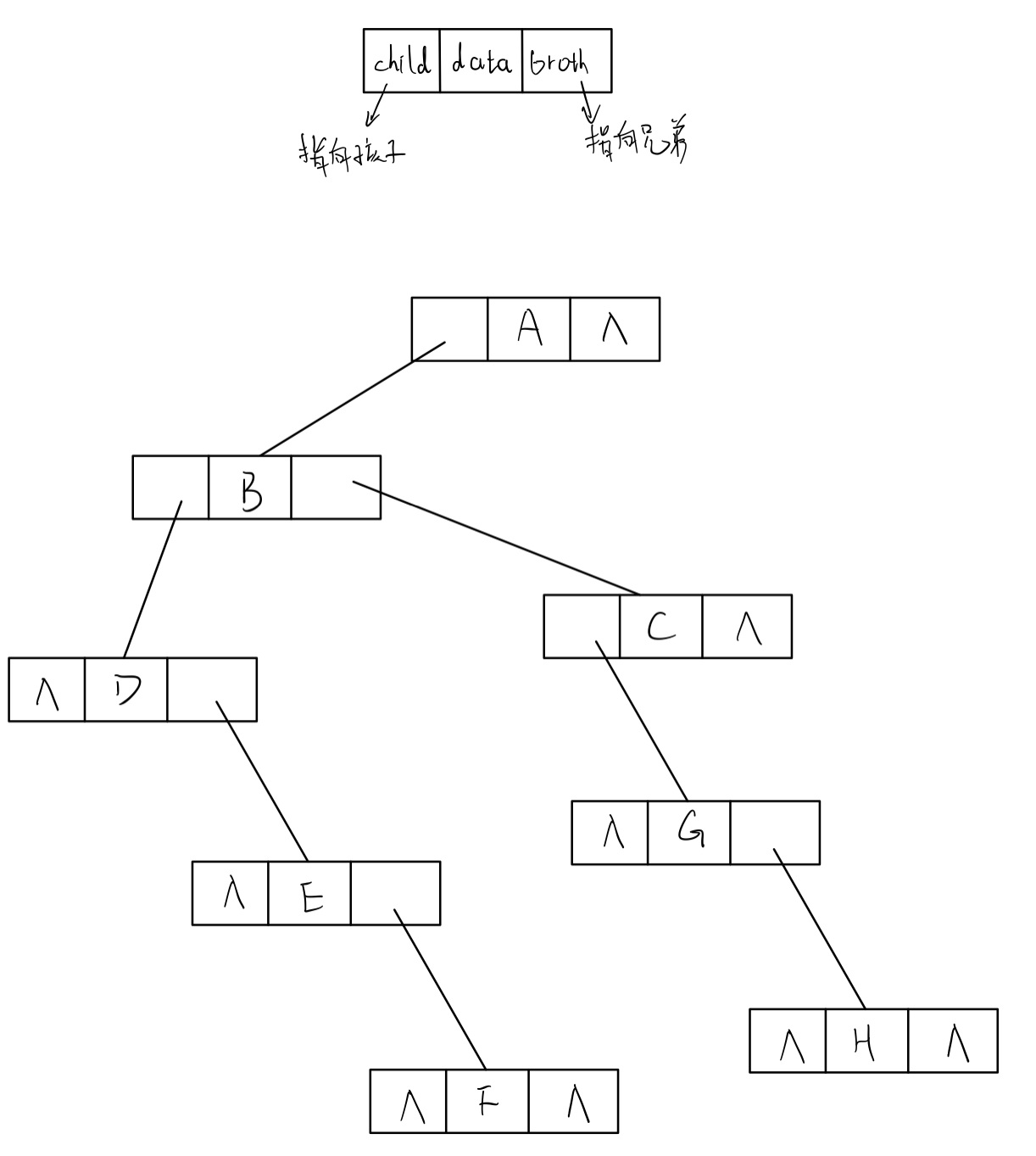
4). Child brother representation

1. data structure

struct BiNode{
    ElemType data;
    BiNode* firstchild;	// Child pointer
    BiNode* nextsibling; // Brother pointer
};

1. Illustration
   

4. Application of tree

Directory structure of file system

II Binary tree

1. Concept

   a binary tree is a finite set of nodes, which is empty or composed of a root node plus two left and right subtrees. Each node consists of at most two subtrees.
   a binary tree is an ordered tree, and the subtree can be divided into left and right.

2. Special binary tree

1. Full binary tree: a binary tree has n layers. The nodes of each layer have reached the maximum value of 2^(n-1). The total number of nodes in the tree is 2^n - 1
   
2. Complete binary tree: a binary tree has n nodes, and each node corresponds to its corresponding full binary tree node, then the tree is a complete binary tree.
   

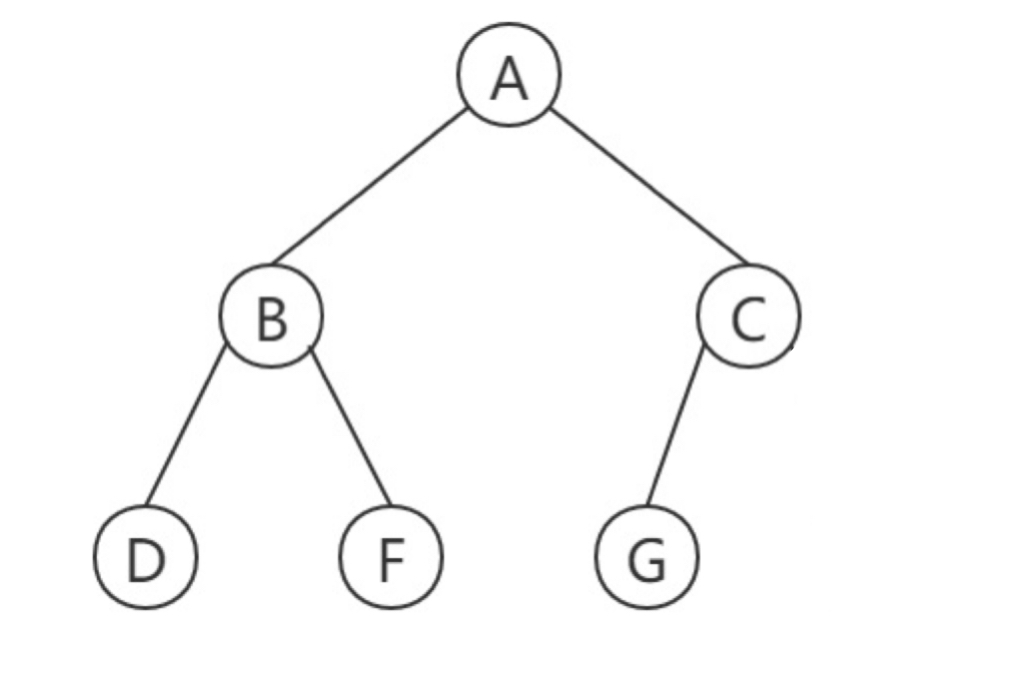
  if the total number of nodes in a complete binary tree is even, only one node has a left child, and the penultimate non leaf node must have only one left child.
  if the total number of nodes in a complete binary tree is odd, all non leaf nodes have two children.

3. Properties of binary tree

1. Property 1: if the number of layers of the specified root node is 1, there are at most 2^(i-1) nodes on layer I of a non empty binary tree

2. Property 2: if the number of layers of the root node is specified as 1, the maximum number of nodes of the binary tree with depth h is 2^h - 1

3. Property 3: for any binary tree, if the number of nodes with degree 0 is n0 and the number of nodes with degree 2 is n2, then n0 = n2 + 1

4. Property 4: if the number of layers of the specified root node is 1, it has the full binary tree depth of N nodes, h=log2(n+1)

5. Property 5: for a complete binary tree with n nodes, if all nodes are numbered from 0 according to the array order from top to bottom and from left to right, the following derivation is made for the node with sequence number i:

    1.if i>0, i The parent serial number of the location is: (i-1)/2;  if i=0,i It is the root node and has no parents
    2.If 2 i+1<n, Serial number is left child: 2i+1, 2i+1>=n Otherwise, there is no left child
    3.If 2 i+2<n, The serial number of the right child is: 2i+2, 2i+2>=n Otherwise, there is no right child
   

Next, according to the above properties, let's look at an example:
  assuming that there are 1000 nodes in a complete binary tree, the tree has multiple leaves, several points, how many branch nodes, and how many nodes have only left children.

	The total number of nodes in a known binary tree n = n0 + n1 + n2;
	Because the total number of nodes in the tree is even, so n1=0
	According to property 3, we know n0 = n2 + 1;
		So it can be concluded that, 
		n = n0 + n2 --> 1000 = n2+1+n2
		therefore n2 = 499, n0 = 500 There is no direct point, only the left node

4. Storage method of binary tree

1). Sequential storage mode

   sequential storage uses array to store the nodes of binary tree, and subscripts represent the relationship between nodes.
   sequential storage is only suitable for storing complete binary trees. Use property 5 to number each node of the binary tree, and the array subscript is the same as the element number.
   if the incomplete binary tree must be stored in a sequential manner, it is necessary to logically supplement the tree as a complete binary tree, and store the tree as a complete binary tree during storage. However, using this form for storage will cause a lot of waste of space. For incomplete binary trees, it is recommended to use the chain form for storage.
The specific implementation will be explained in detail in the following

2). Chain storage mode

   express the relationship between nodes in the form of pointer, such as the representation of tree in the above. The specific content will be explained in detail below.

III Sequential structure and implementation of binary tree (heap)

1. Concept of reactor

  store all elements in a one-dimensional array in the order of a complete binary tree. And the tree should meet the following conditions: for any node, if the node value is larger than its child node, it is called large root heap. If the node value is smaller than any of its children, it is called small root heap.

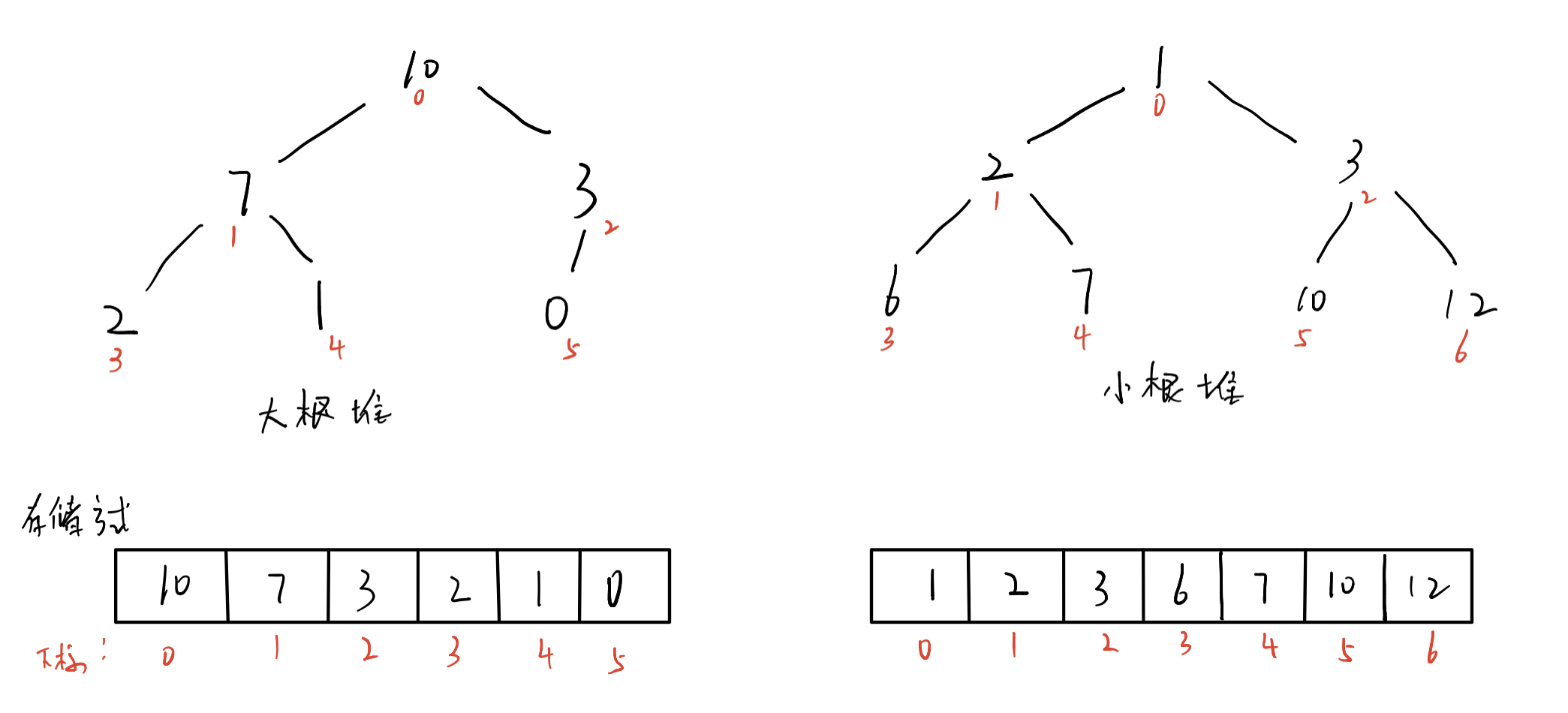
2. Nature of reactor

1 The top element must be the smallest or largest element in the heap
2 The tree structure stored in the heap must be a complete binary tree
3 Heap order is ascending or descending(Path from root node to leaf node)
4 The parent node is smaller than any of its descendants(large)

3. Implementation of heap

   when implementing heap, an array is given. Logically, this array can be regarded as a complete binary tree, but the tree form of this array may not meet the definition of heap. Therefore, some algorithms are needed to adjust this array to an array that conforms to the nature of heap.
  here we introduce the downward adjustment algorithm of pair.

1). Downward adjustment algorithm of heap

1. Ideas:
   judge whether each parent node meets the requirements of being greater than or less than its child nodes. If it needs to be exchanged, exchange two nodes. After the exchange, it may still not meet the heap characteristics. Therefore, move the location of the parent node and child node to continue to judge whether the characteristics are met until the heap characteristics are met. This adjustment is over.

   the following example shows that the left and right subtrees meet the heap characteristics, but the root node does not meet the heap characteristics, so only the root node needs to be adjusted.

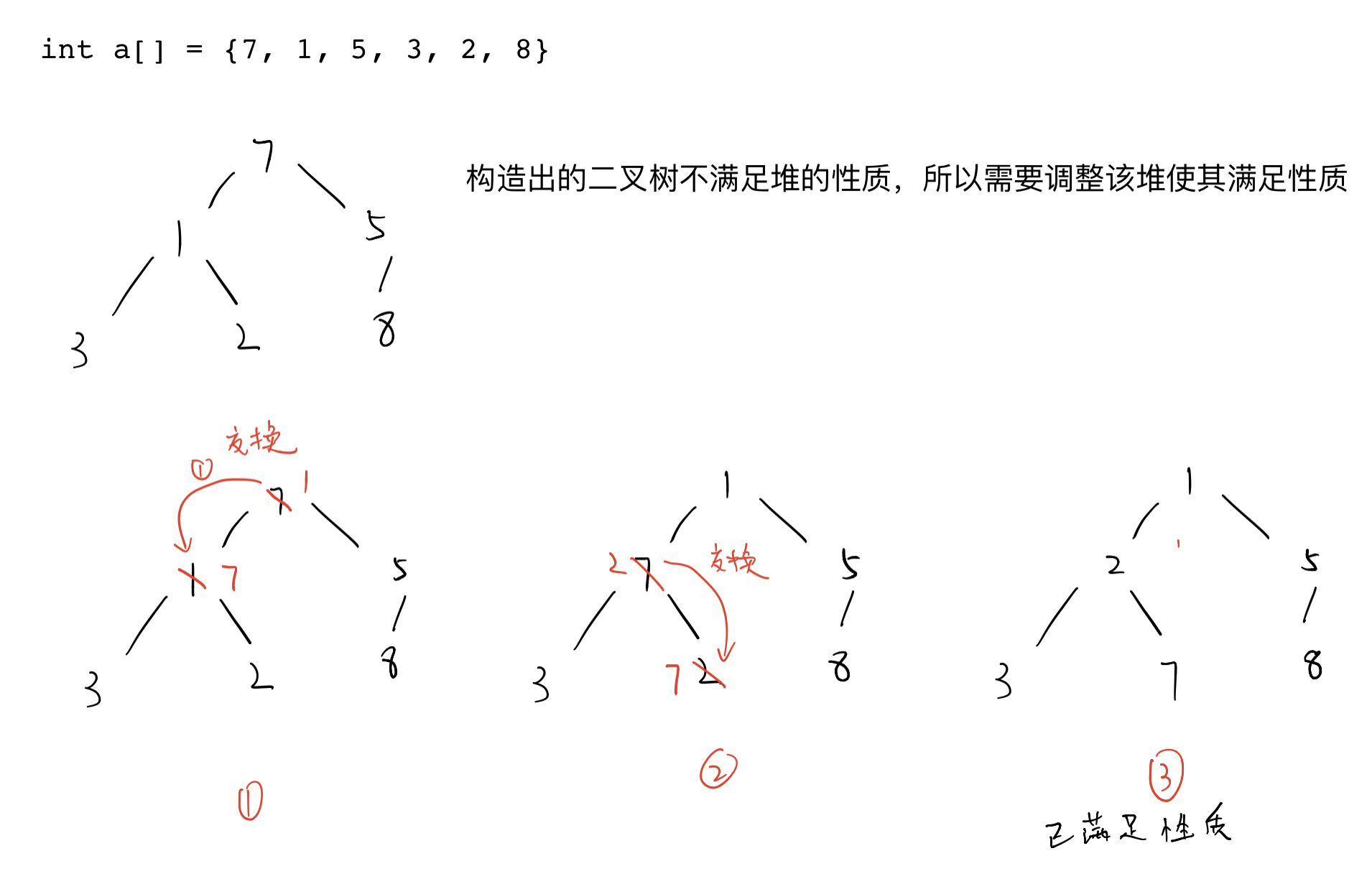
2. Code implementation

// Downward adjustment algorithm of heap:
// The incoming node is a parent node. Judge whether the current parent node meets the nature of the heap. If not, compare the current parent node with the child node
// If there are two children, exchange positions with the children with smaller values, and compare them in this way until they reach the leaf node or exit without meeting the conditions
void AdjustDown(Heap* hp, int nodeId)
{
	HPDataType* data = hp->_a;
	int child = 2 * nodeId + 1;

	while (child < hp->_size)
	{
		// Find the small value of the two children
		if (child + 1 < hp->_size && hp->_cmp(data[child + 1], data[child]))
			child++;

		// Judge whether the nodes in the subtree meet the nature of the heap, and exchange if not
		if (hp->_cmp(data[child], data[nodeId]))
		{
			Swap(&data[nodeId], &data[child]);

			// After the node is exchanged, the lower subtree may not meet the nature of the heap, so move the position of the parent node and the child node and continue to judge
			nodeId = child;
			child = 2 * nodeId + 1;
		}
		else
		{
			return;
		}
	}
}

2). Heap creation

  the process of creating a heap is actually the process of adjusting an array to conform to the nature of the heap, which is exactly the same as the downward adjustment process of the heap.

Find the penultimate non leaf node `lastNotLeaf = ((size-1)-1)/2`
From this node to the root node, the downward adjustment algorithm is applied to each node one by one

Code part:

void HeapCreate(Heap* hp, HPDataType* a, int n, CMP cmp)
{
	// initialization
	hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (NULL == hp->_a)
	{
		assert(0);
		return;
	}
	hp->_size = 0;
	hp->_capacity = n;
	hp->_cmp = cmp;

	// Import data
	memcpy(hp->_a, a, sizeof(HPDataType) * n);
	hp->_size = n;

	// Using the downward adjustment algorithm, adjust the heap to conform to the nature of the heap, and traverse from the parent node of the penultimate node to the root node
	for (int root = (n - 2) / 2; root >= 0; root--)
	{
		AdjustDown(hp, root);
	}
}

3). Heap insertion

The heap insertion process is

1 Check whether the heap space is sufficient. If not, it needs to be expanded
2 Inserting elements into the tail of the heap may destroy the characteristics of the heap
3 Use the upward adjustment algorithm for the inserted elements, and compare them by seeking parents from children

Heap up adjustment algorithm
  this algorithm is consistent with the downward adjustment algorithm and will not be repeated.

Figure displaying the heap insertion process:

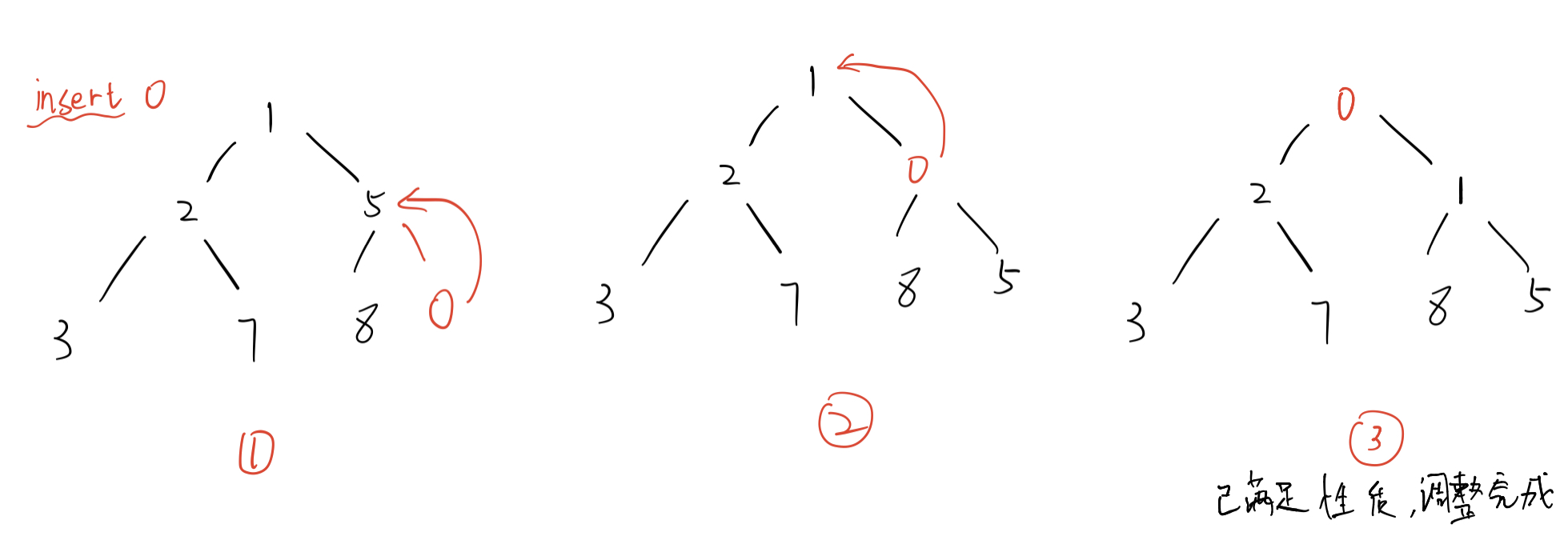
Code part

void CheckCapacity(Heap* hp)
{
	if (hp->_size == hp->_capacity)
	{
		hp->_a = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * hp->_capacity * 2);
		if (NULL == hp->_a)
		{
			assert(0);
			return;
		}

		hp->_capacity *= 2;
	}
}

// Upward adjustment algorithm
// The same idea, the incoming node is the child node, determines whether the relationship between the child and the parents satisfies the conditions, and satisfies one by one until the root node or the condition is not satisfied.
void AdjustUp(Heap* hp, int nodeId)
{
	HPDataType* data = hp->_a;
	int parent = (nodeId - 1) / 2;

	while (nodeId > 0)
	{
		if (parent >= 0 && hp->_cmp(data[nodeId], data[parent]))
		{
			Swap(&data[parent], &data[nodeId]);

			nodeId = parent;
			parent = (nodeId - 1) / 2;
		}
		else
		{
			return;
		}
	}
}

// Heap insertion
// Judge whether the space is enough. If the space is enough, insert the element into the tail of the queue to judge whether the node meets the nature of the heap. If not, adjust it upward to meet the nature
void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);

	// Capacity expansion
	CheckCapacity(hp);

	// Insert element at the end of the queue
	hp->_a[hp->_size++] = x;

	AdjustUp(hp, hp->_size - 1);
}

4). Delete operation of heap

   in the process of deleting the heap, delete the heap top element. When deleting the heap top element, in order to simplify the process, use the following ideas to delete the heap top element:

1 Swap top and tail elements
2 Delete heap tail element
3 Then, the downward adjustment algorithm is used for the top element of the heap to make it conform to the characteristics of the heap.

Figure displaying the deletion process:



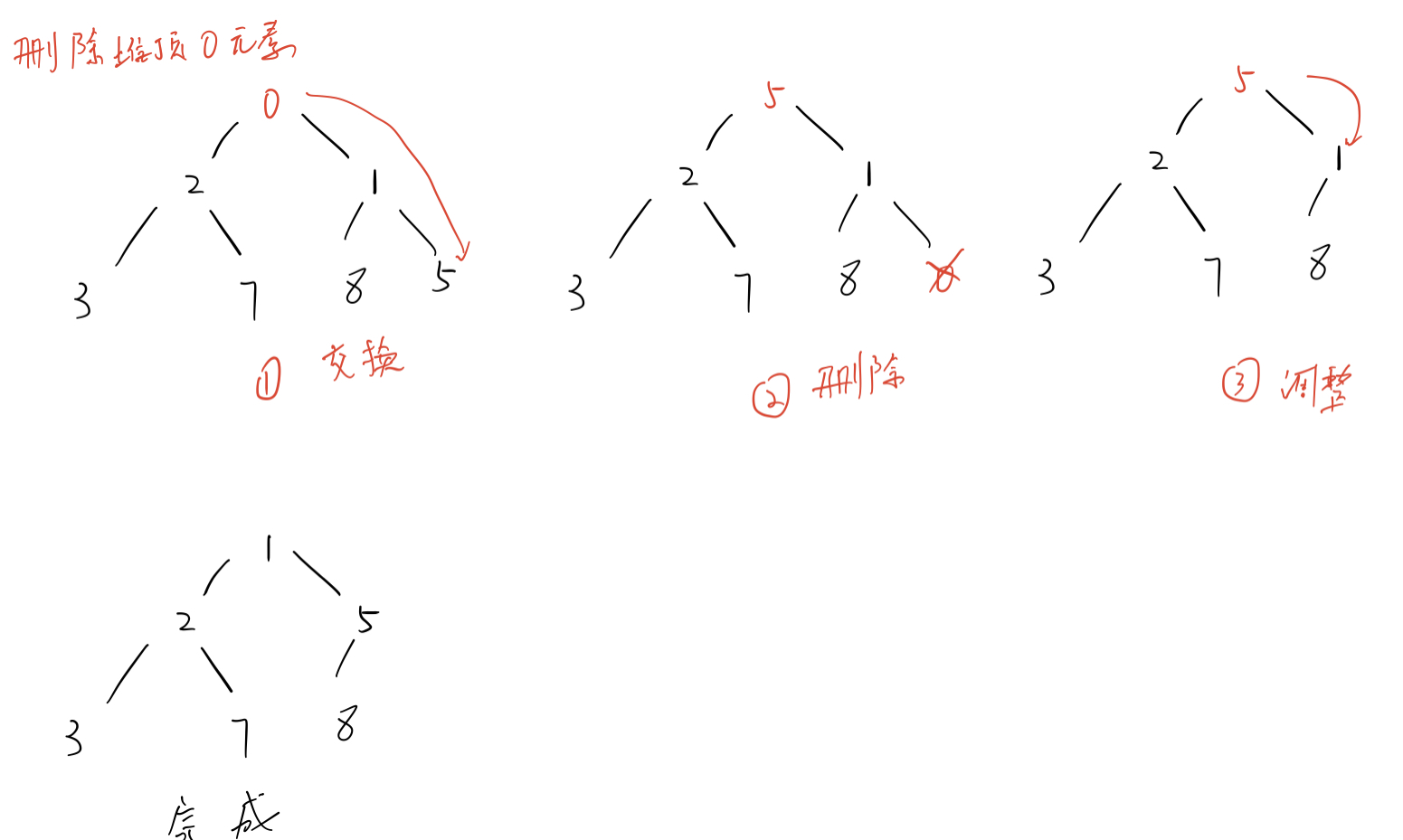
Code part

// Deletion of heap
// Delete from the heap head, exchange the heap head and tail elements, and ignore the queue tail elements. Because the structure of the heap is adjusted, the heap may not meet its properties,
// Therefore, adjust the root node downward
void HeapPop(Heap* hp)
{
	HPDataType* data = hp->_a;
	
	Swap(&data[0], &data[hp->_size - 1]);
	hp->_size--;

	AdjustDown(hp, 0);
}

4. Application of reactor

Application 1: heap sorting

  sort the heap by using the idea of deleting the heap. The process of deleting the heap is to exchange the heap head element with the heap tail element. The heap head element is the maximum or minimum value in the heap, so each time the maximum or minimum value is moved to the heap tail. After the movement is completed, the downward adjustment algorithm is used.
  when each element goes through the above process, the heap becomes orderly.
  it should be noted that large root piles are built in ascending order and small root piles are built in descending order.

Illustration

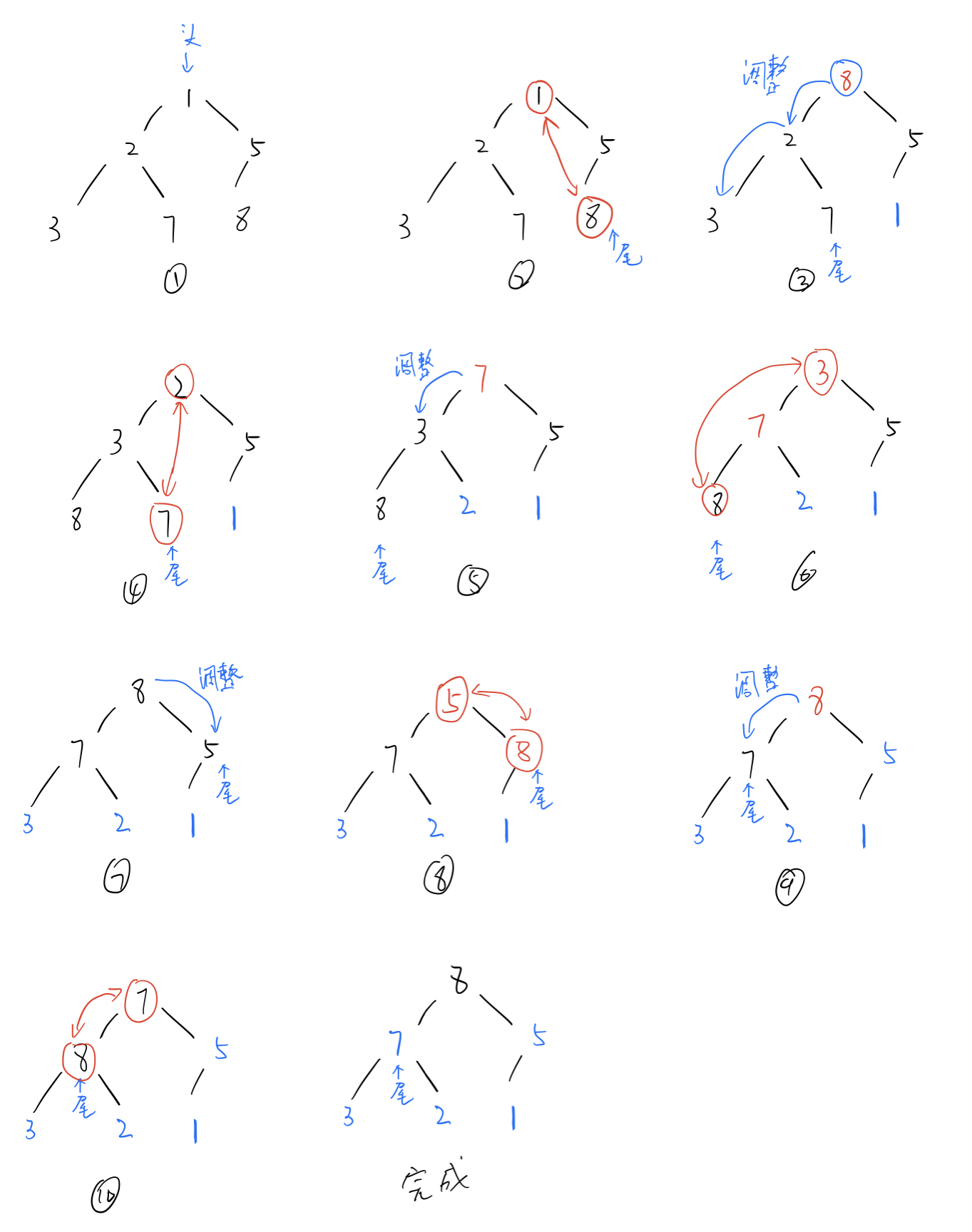
code implementation

// Idea:
//		1. First build a large or small pile of n elements
//		2. After completion, the stacking head elements are either the largest or the smallest
//		3. Exchange the stack head elements with the stack tail elements, and eliminate the queue tail elements,
//	    4. Repeat the above process until all elements in the heap are eliminated

// Heap sort array
void HeapSort(int* a, int n, CMP cmp)
{
	Heap hp;
	// Build pile
	HeapCreate(&hp, a, n, cmp);

	// Place the heap head element at the end of the heap and eliminate the element. This operation is the same as deleting the heap element
	while (hp._size > 0)
	{
		HeapPop(&hp);
	}

	for (int i = 0; i < n; i++)
	{
		printf("%d ", hp._a[i]);
	}
	printf("\n");
}

Top-K application

   find the minimum or maximum first k data, eg: the maximum 10 elements in the data set. Usually, this kind of problem will provide a huge amount of data. The time complexity of using ordinary sorting is the lowest, which is O(logn). Therefore, heap is used to solve the Top-k problem, and the time complexity is O(n)

thinking
  1. Use the first k elements to build a heap, take the minimum value to build a large heap, and take the maximum value to build a small heap.
  2. Use the remaining n-k elements to compare with the elements at the top of the heap in turn. If the conditions are met, exchange the two values. After the exchange, use the downward adjustment algorithm to make it meet the heap characteristics. Repeat the above operations until the comparison is completed. Because the heap top element is either the maximum or the minimum.

Illustration

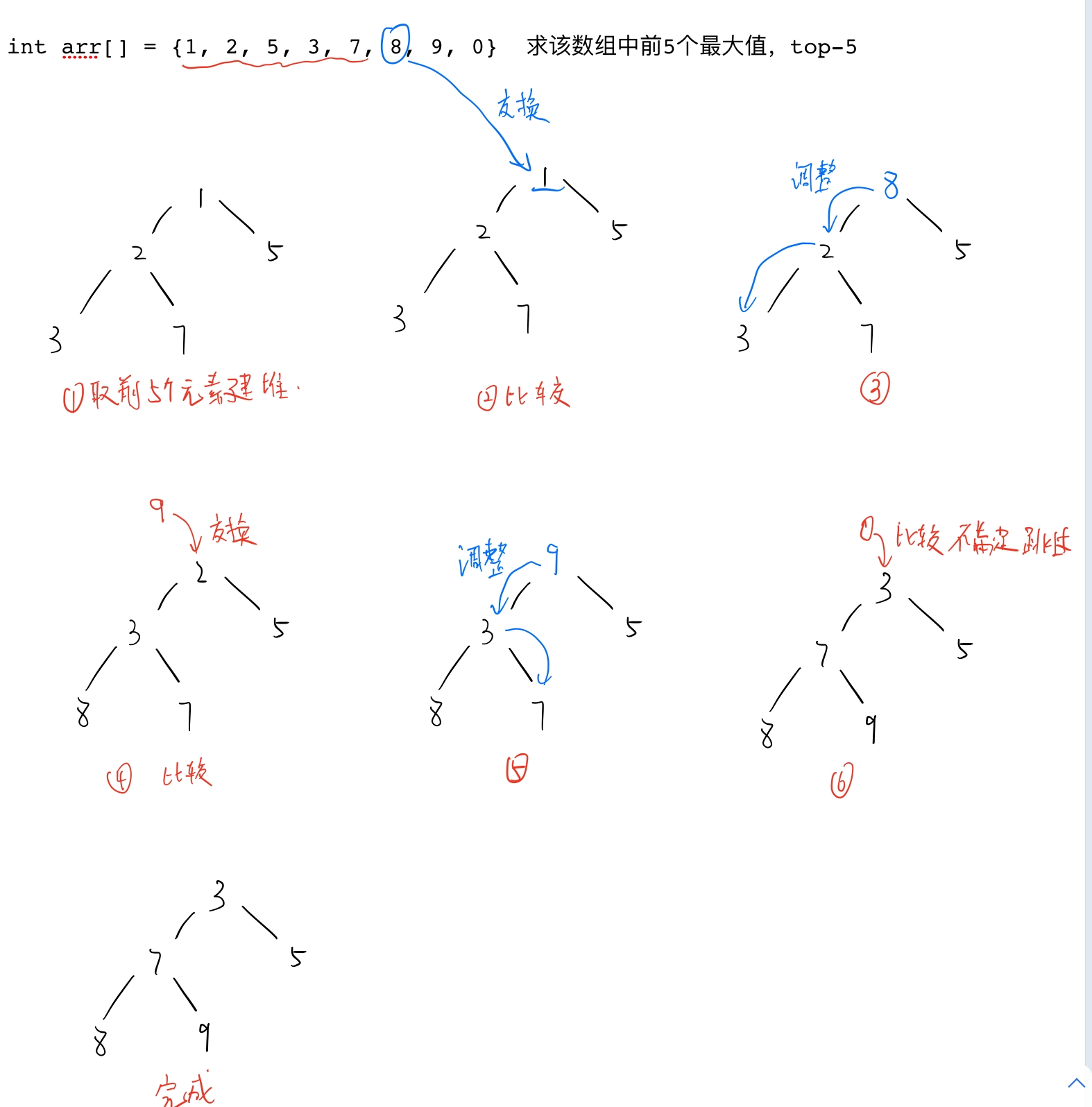
code implementation

// Find the largest first k and create a small heap of K
// Find the smallest first k and establish a number of K
// Idea: 1. Build the reactor with the first k elements
//		 2 use the remaining n-k elements to compare with the top element in turn. If the top element is greater than / less than this element,
//  		Then the element is replaced with the top element of the heap. After replacement, the downward adjustment algorithm is used to adjust the compliance of the heap
// Calculate the top-k maximum or minimum according to the user's choice
void PrintTopK(int* a, int n, int k, CMP cmp)
{
	Heap hp;
	// Build pile
	HeapCreate(&hp, a, k, cmp);

	// Compare n-k elements with the top of the heap
	for (int i = k; i < n; i++)
	{
		if (hp._cmp(hp._a[0], a[i]))
		{
			// Swap header elements
			Swap(&(hp._a[0]), &a[i]);

			// Downward adjustment
			AdjustDown(&hp, 0);
		}
	}

	for (int i = 0; i < k; i++)
	{
		printf("%d ", hp._a[i]);
	}
}

void TestTopk()
{
	int arr[] = { 42, 65, 12, 65, 12, 56, 654, 12, 654, 12312, 656, 12,1, 233, 3, 5, 6, 7, 8,100 ,9 ,10 };
	int k = 0;
	int flag = 0;

	printf("Input format: num1 num2 ---> num1 How many first digits are displayed,  num2 Show Max or min, Max 1 min 0\n");
	printf("Please enter parameters:> ");
	scanf("%d %d", &k, &flag);

	if(1 == flag)
		PrintTopK(arr, sizeof(arr) / sizeof(arr[0]), 5, Less);
	else
		PrintTopK(arr, sizeof(arr) / sizeof(arr[0]), 5, Greater);
}

IV Chain storage of binary tree

1. Chain storage structure of binary tree

struct BiTreeNode
{
	DataType data;
	BiTreeNode* lchild;	// Point to left child
	BiTreeNode* rchild; // Point to the right child
};

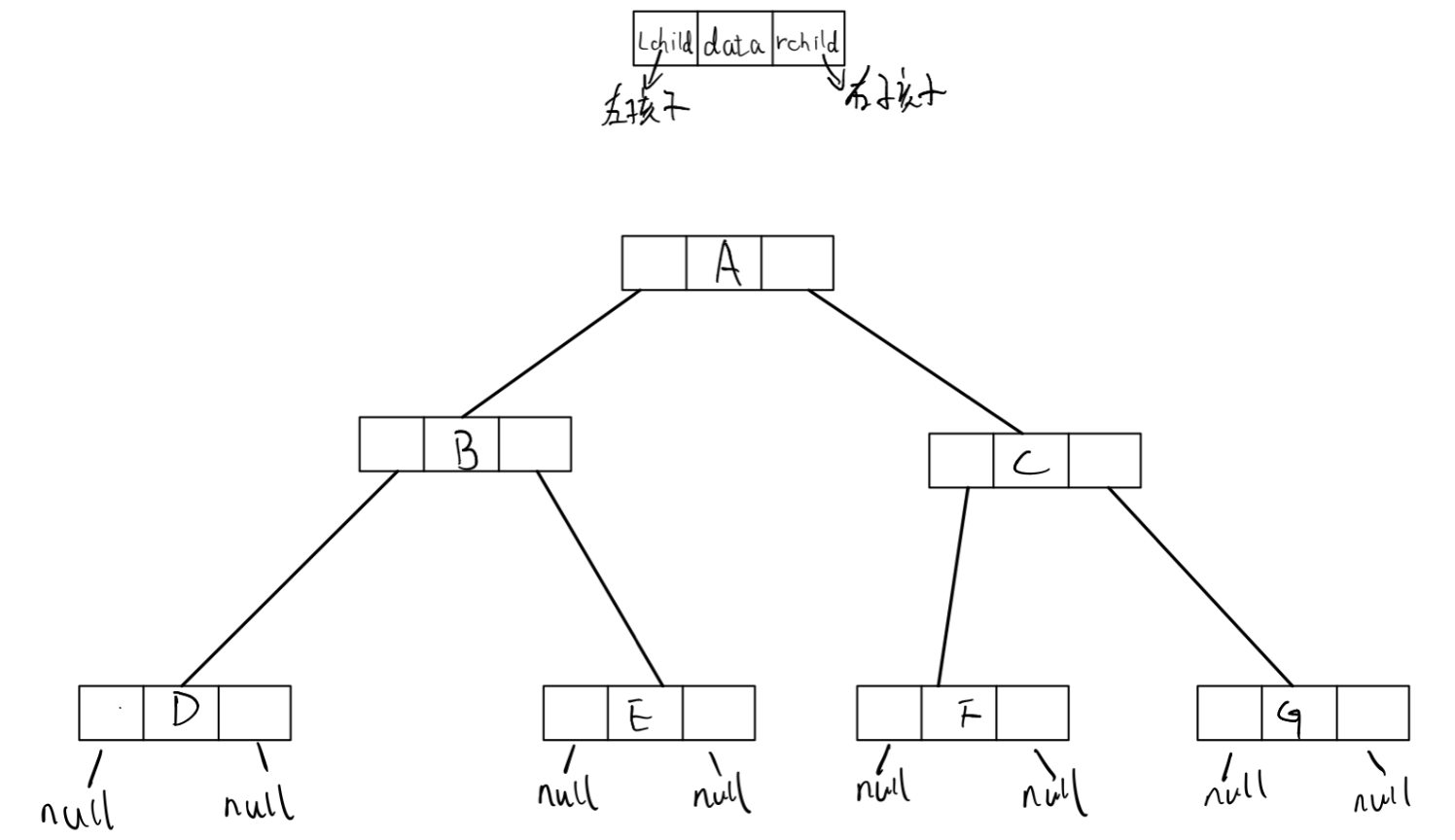
2. Traversal of binary tree

   traversal refers to performing some corresponding operation on the nodes in the binary tree according to a specific rule, and each node operates only once.

   there are three traversal methods in binary tree, and the naming method is named according to the access order of the root node. Traversing the tree recursively.

1). Preorder traversal
  first access the root node, then the left subtree, and finally the right subtree. (root left right)
2). Middle order traversal
  access the left subtree first, then the root node, and finally the right subtree. (left root right)
3). Preorder traversal
  access the left subtree first, then the right subtree, and finally the root node. (left right root)

Illustration
Examples of using middle order traversal:

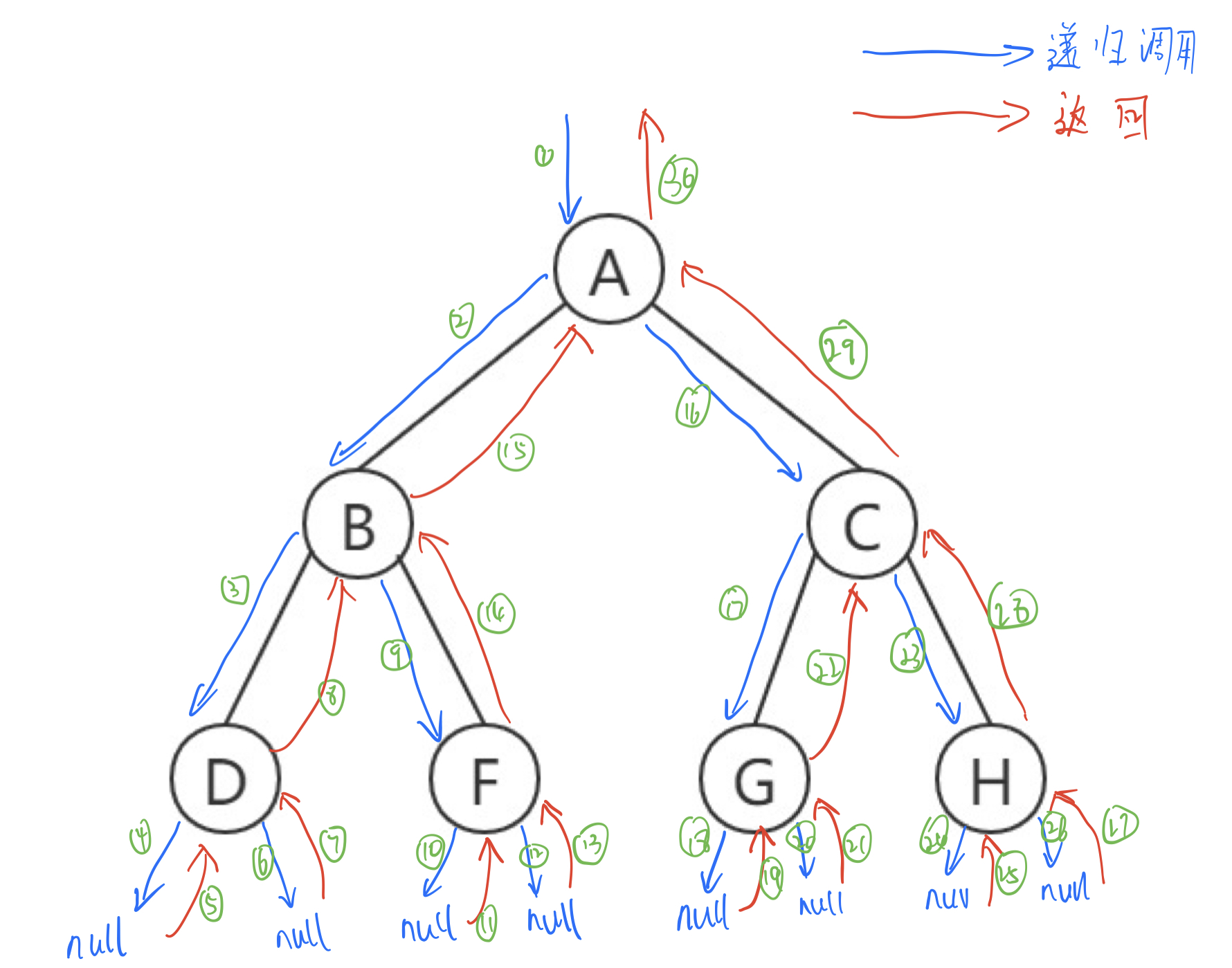
The above figure is an example:

Preorder traversal: A B D F C G H
 Middle order traversal: D B F A C G H
 Postorder traversal: D F B C G H A

code implementation

// Preorder traversal binary tree
void PreOrderTraversal(BTNode* bt, int level)
{
	if (bt != NULL)
	{
		Vist(bt->data, level);
		PreOrderTraversal(bt->lchild, level + 1);
		PreOrderTraversal(bt->rchild, level + 1);
	}
}

// Middle order traversal
void InOrderTraversal(BTNode* bt, int level)
{
	if (bt != NULL)
	{
		InOrderTraversal(bt->lchild, level + 1);
		Vist(bt->data, level);
		InOrderTraversal(bt->rchild, level + 1);
	}
}

// Postorder traversal
void PostOrderTraversal(BTNode* bt, int level)
{
	if (bt != NULL)
	{
		PostOrderTraversal(bt->lchild, level + 1);
		PostOrderTraversal(bt->rchild, level + 1);
		Vist(bt->data, level);
	}
}

4). Sequence traversal of binary tree
   this traversal method is better understood, which is to output the elements of each layer from left to right. However, its implementation is completely different from the above three traversal methods.
   because to realize sequence traversal, it is necessary to store all child nodes of each layer. If the depth of the tree is large, the amount of data is huge. Therefore, in sequence traversal, queue is used to traverse the sequence of binary tree.
For queue operations, click here Queue operation

Sequence traversal process

1. Define a queue structure and initialize it to queue the root node.
2. Take out the queue head node from the queue head, traverse the left and right subtrees of the node, and join the left and right subtrees into the queue.
3. Cycle the above operation until the queue is empty.

Illustration

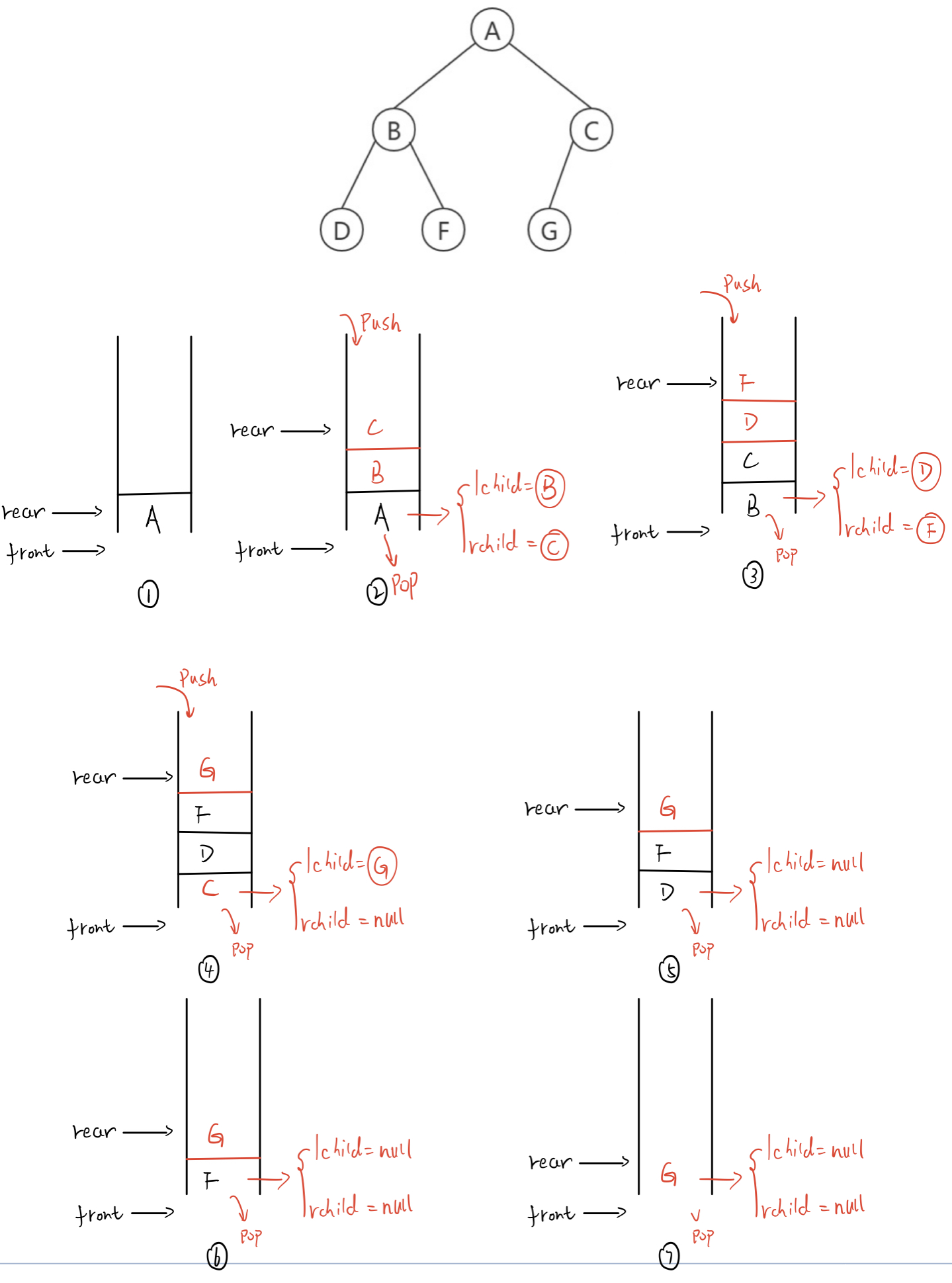
code implementation

// Sequence traversal starts from the first layer and traverses the nodes from left to right according to the hierarchical relationship of the tree.
// When traversing, make use of the characteristics of the queue to queue the root node first, then traverse the root nodes of the left and right subtrees, and add the left and right subtrees to the queue nodes.
void BinaryTreeLevelOrder(BTNode* root)
{
	if (NULL == root)
		return;

	Queue queue;

	// Initialize a queue and add the root node to the queue
	QueueInit(&queue);
	QueuePush(&queue, root);

	// Traverse the left and right subtrees of the root node and output
	while (!QueueEmpty(&queue))
	{
		BTNode* cur = QueueFront(&queue);
		PrintNodeData(cur);

		// Queue the left and right subtrees of the root node
		if (NULL != cur->_left)
			QueuePush(&queue, cur->_left);

		if (NULL != cur->_right)
			QueuePush(&queue, cur->_right);

		QueuePop(&queue);
	}

	QueueDestroy(&queue);
}

3. Other operations of binary tree

1). Create tree

   the creation process of binary tree is the same as the above traversal process. Here, we use the preorder traversal method of binary tree to create binary tree.
   in the process of creating the tree, the data of the incoming array should be read. Because the recursive method is adopted, it should be noted that when passing the subscript, it should be passed through the address

// The binary tree is constructed through the array "ABD##E#H##CF##G##" traversed in the previous order
// If pi is passed by value, because it is a local variable, the modified value will not be brought out after each modification.
// During recursion, in order to protect the scene, the content of the last execution of the function is put on the stack. After the recursion of the function is completed, it will step out of the stack step by step, so the value transfer cannot bring out the result
BTNode* _BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	if (a[*pi] == '#' || *pi > n)
	{
		(*pi)++;
		return NULL;
	}

	BTNode* root = BuyBinTreeNode(a[(*pi)++]);

	root->_left = _BinaryTreeCreate(a, n, pi);
	root->_right = _BinaryTreeCreate(a, n, pi);

	return root;
}

BTNode* BinaryTreeCreate(BTDataType* a, int n)
{
	int index = 0;

	return _BinaryTreeCreate(a, n, &index);
}

2). Calculate the number of nodes in the tree

   calculating the number of nodes is also realized by recursion. Calculate the number of nodes of the left and right subtrees of the root node respectively, and finally add them to get the result.

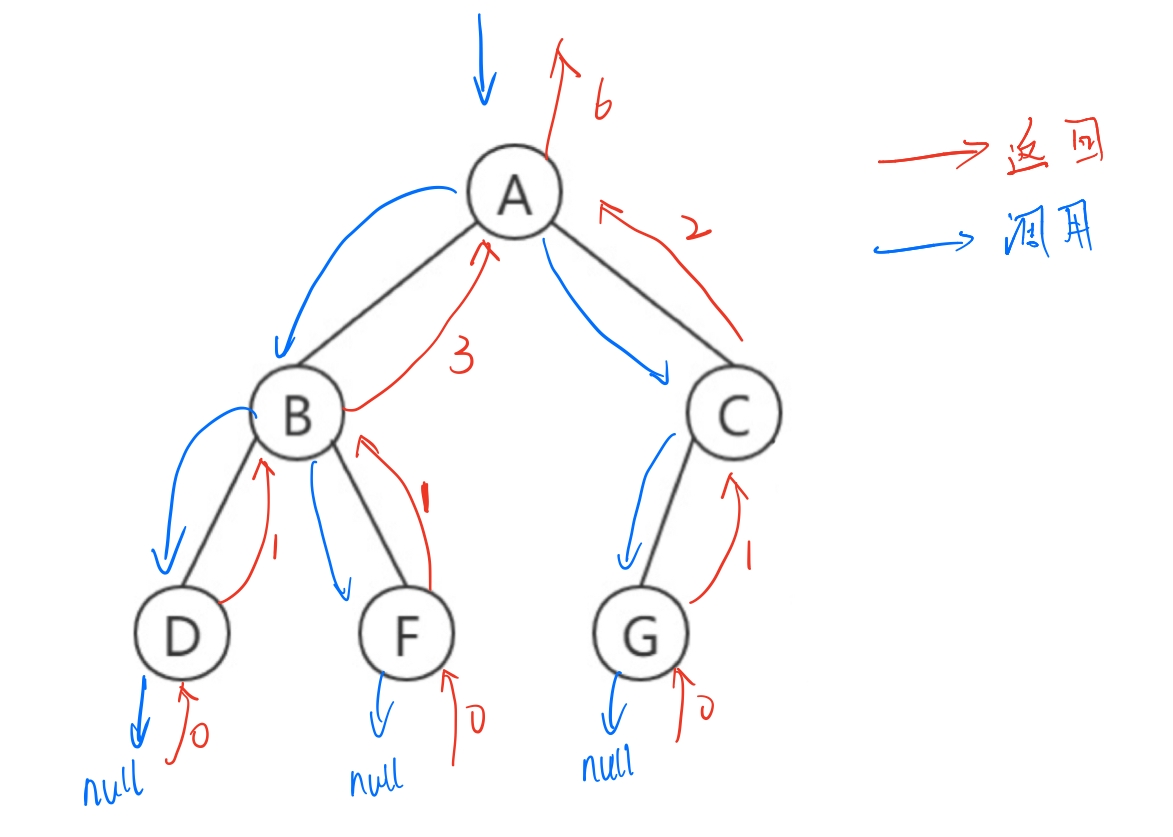
// Traversal of left and right subtrees, recursive traversal
int BinaryTreeSize(BTNode* root)
{
	if (NULL == root)
		return 0;

	return BinaryTreeSize(root->_lchild) + 
		   BinaryTreeSize(root->_rchild) + 1;
}

3). Find the number of nodes in the k-th layer

   if you directly calculate the number of elements in layer K, it is difficult to solve, so you can solve the number of child nodes through layer k-1.

thinking

1. Tree empty or k<0, Cannot be calculated. k = 1, It means that there is only root node.
2. Find No k-1 For the nodes of the layer, find the total number of child nodes.

code

// Calculate the number of points in layer K through layer k-1
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if(NULL == root || k < 0)
	{
		return 0;
	}

	if(NULL != root && 1 == k)
	{
		return 1;
	}
	
	return BinaryTreeLevelKSize(root->_lchild, k - 1) + 
	   	   BinaryTreeLevelKSize(root->_rchild, k - 1);
}

4). Find the number of leaf nodes

   it is basically the same as the above method. When the left and right subtrees are empty, they are leaf nodes

int BinaryTreeLeafSize(BTNode* root)
{
	if(NULL == root)
	{
		return 0;
	}

	if(NULL == root->_lchild&& NULL == root->_rchild)
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->_lchild) + 
		   BinaryTreeLeafSize(root->_rchild);
}

5). Calculate the height of the tree

   the tree contains left subtree and right subtree, so you only need to calculate the height of the left and right subtrees and take the maximum value.

int BinaryTreeHeight(BTNode* root)
{
	if(NULL == root)
	{
		return 0;
	}
	
	int lHeight = BinaryTreeHeight(root->_lchild);
	int rHeight = BinaryTreeHeight(root->_rchild);

	return lHeight > rHeight ? lHeight + 1 : rHeight + 1;
}

6). Finds the specified element in the tree

   the idea is still the same. Find the specified elements from the left and right subtrees respectively.

// The binary tree finds the node with the value of x
// Find node values through sequential traversal
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (NULL == root)
		return NULL;

	if (root->_data == x)
	{
		return root;
	}

	// First recursively find the left subtree, and then recursively find the right subtree. If found, a non null value will be returned, and the bool operation in this step will be true
	return BinaryTreeFind(root->_left, x) || BinaryTreeFind(root->_right, x);
}

7). Destroy tree

   destroy the tree by post order traversal. If other traversal methods are used, the root node of the subtree will be destroyed first, resulting in the failure of subsequent destruction, so the post order traversal method is used to destroy the tree.

// Binary tree destruction
// After traversing the binary tree, destroy the leaf node first, and then the root node
void BinaryTreeDestory(BTNode** root)
{
	assert(root);

	if (NULL == *root)
		return;

	BinaryTreeDestory(&(*root)->_left);
	BinaryTreeDestory(&(*root)->_right);

	free(*root);
	*root = NULL;
}

8). Judge whether the binary tree is a complete binary tree

   the node positions of complete binary tree and full binary tree are the same, and the last layer is arranged from left to right. Therefore, we only need to find the location of the last unsaturated node, and subsequent nodes cannot have children.

Two methods are provided

// Judge whether the binary tree is a complete binary tree
// The same idea as sequence traversal requires queue operation
// The nodes of a complete binary tree can be divided into the following cases
//	1. If both the left and right subtrees of the root node exist, there will be no impact on the next node, so continue to queue the subtrees of the root node
//  2. The left subtree and the right subtree of the root node do not exist, OR the left and right subtrees of the root node do not exist
//    In this case, the root node of the last node is satisfied for the above node, but it is not satisfied for other cases,
//    Therefore, the flag bit is added in this case. When the conditions are not met, the flag bit is activated,
//    The next cycle needs to judge the flag bit. If the flag bit is activated and the left and right subtrees of the next node are empty, it has no effect. If the subtree of the next node is not empty, it means that the tree does not satisfy the complete binary tree
int BinaryTreeComplete(BTNode* root)
{
	// If the tree is empty, it is also a complete binary tree
	if (NULL == root)
		return 1;

	// Initialize queue
	Queue queue;
	QueueInit(&queue);
	QueuePush(&queue, root);

	int flag = 0;

	// If both left and right nodes exist, the next node will be traversed. If the left child exists but the right child does not exist, it will be marked,
	while (!QueueEmpty(&queue))
	{
		BTNode* cur = QueueFront(&queue);

		// Situation II
		if ((NULL != cur->_left && NULL == cur->_right) || (NULL == cur->_left && NULL == cur->_right))
		{
			flag = 1;
		}

		// Situation III
		if (NULL == cur->_left && NULL != cur->_right)
		{
			QueueDestroy(&queue);
			return 0;
		}

		// Situation II
		if (flag && (NULL != cur->_left) && NULL != cur->_right)
		{
			QueueDestroy(&queue);
			return 0;
		}

		if (NULL != cur->_left)
		{
			QueuePush(&queue, cur->_left);
		}

		if (NULL != cur->_right)
		{
			QueuePush(&queue, cur->_right);
		}

		QueuePop(&queue);
	}

	QueueDestroy(&queue);
	return 1;
}

int BinaryTreeComplete2(BTNode* root)
{
	// If the tree is empty, it is also a complete binary tree
	if (NULL == root)
		return 1;

	// Initialize queue
	Queue queue;
	QueueInit(&queue);
	QueuePush(&queue, root);

	int flag = 0;

	// If both left and right nodes exist, the next node will be traversed. If the left child exists but the right child does not exist, it will be marked,
	while (!QueueEmpty(&queue))
	{
		BTNode* cur = QueueFront(&queue);

		if (flag)
		{
			// After the first unsaturated node, all nodes cannot have children
			if (cur->_left || cur->_right)
			{
				QueueDestroy(&queue);
				return 0;
			}
		}
		else
		{
			// Find the first unsaturated node
			if (cur->_left && cur->_right)
			{
				QueuePush(&queue, cur->_left);
				QueuePush(&queue, cur->_right);
			}
			else if (cur->_left)
			{
				QueuePush(&queue, cur->_left);
				flag = 1;
			}
			else if (cur->_right)
			{
				QueueDestroy(&queue);
				return 0;
			}
			else
			{
				flag = 1;
			}
		}

		QueuePop(&queue);
	}

	QueueDestroy(&queue);
	return 1;
}

V Given two traversal methods to determine the tree shape

   there are many topics that give two traversal methods, determine the tree shape through these two traversal methods, and find the result of another traversal. The following will describe in detail how to determine another traversal result in two ways.

1. Pre sequence + middle sequence

Solving steps

1. Find the root node according to the previous traversal.
2. Find the position of the root in the result of the middle order traversal, and divide the result of the middle order traversal into two sequences by this position. The left side of this position is the midpoint of the left subtree of the root, and the right side of this position is the midpoint of the right subtree of the root.
3. Recursively restore the left and right subtrees.

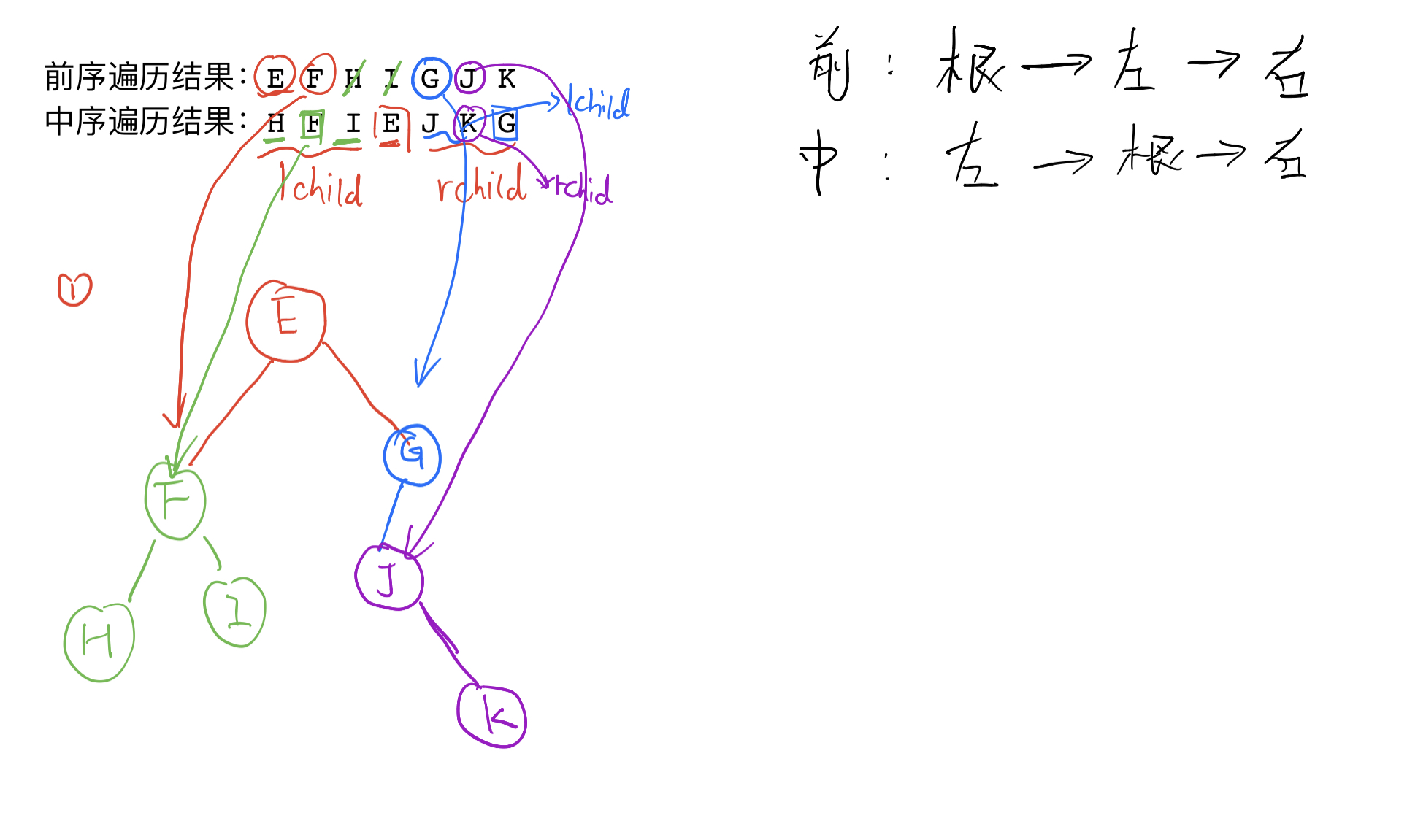
2. Intermediate sequence + subsequent sequence

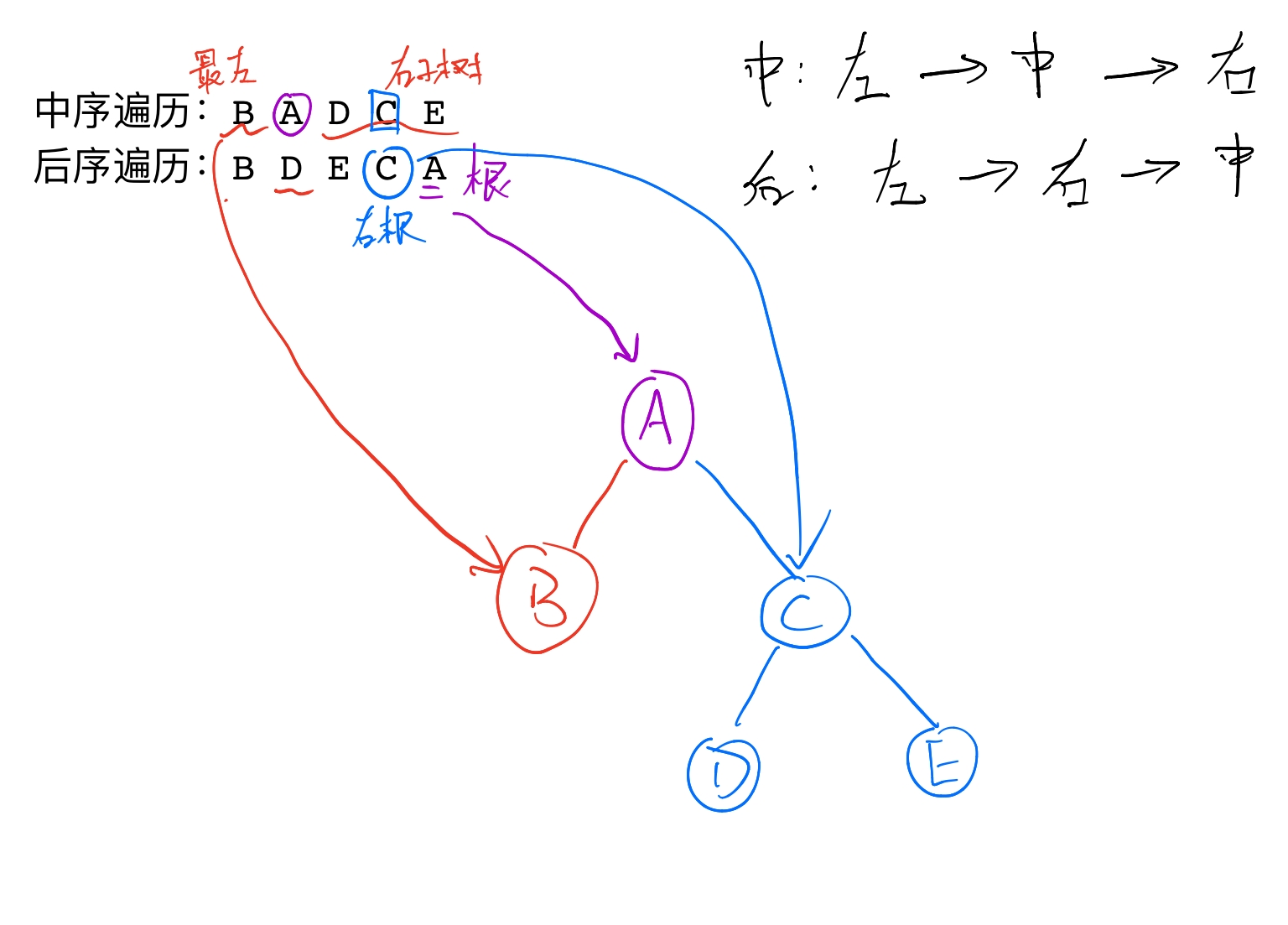
3. Pre sequence + Post sequence

   preamble: Root - > left - > right
   subsequent sequence: left - > right - > root
   when these two traversal methods are combined, it is impossible to distinguish the left and right subtrees, so when these two methods appear, don't bother to take the calculation tree shape, which is futile.

Vi summary

   all the above contents are all the knowledge points related to trees. Some mistakes are inevitable. You are welcome to criticize and correct.