Title Description:

Source: LeetCode
Link: https://leetcode-cn.com/problems/shu-zu-zhong-chu-xian-ci-shu-chao-guo-yi-ban-de-shu-zi-lcof/

• A number in the array appears more than half the length of the array. Please find out this number.
• You can assume that the array is non empty and that there are always many elements in a given array.

Example:

• Example 1:

input: [1, 2, 3, 2, 2, 2, 5, 4, 2]
output: 2

• Tips:

     1 <= Array length <= 50000

Analysis idea 1: hash table statistics

• Official idea - hash table.

• You can use a hash table to quickly count the number of occurrences of each element. Use a HashMap to store each element and the number of occurrences. For each key value pair in the hash map, the key represents an element and the value represents the number of occurrences of the element.

Code (python3)

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        counts = collections.Counter(nums)
        return max(counts.keys(), key=counts.get)

Code (cpp)

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        unordered_map<int, int> count; // Create hash table
        int majority = 0, res = 0;     // Declare variable
        for (int num: nums) {  // Loop through the array nums and add each element in the array to the hash map
            ++count[num];
            if (count[num] > res) { // Traverses all key value pairs in the hash map
                majority = num;
                res = count[num];
            }
        }
        return majority; // Key with the largest return value
    }
};

• perhaps

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        unordered_map <int,int> map;
        for(int n:nums)   
            if(++ map[n] > nums.size()/2)  
            	return n;         
        return -1;
    }
};

Complexity analysis:

• Time complexity: O(n), where n is the length of array nums. We traverse the array nums once. For each element in nums, it only takes constant time to insert it into the hash table.
• Space complexity: O(n).

Analytical thinking 2: sorting

• Official thinking - ranking.

• If all elements in array nums are sorted in monotonic increasing or decreasing order, the elements with subscript ⌊ n/2 ⌋ (subscript starts from 0) must be mode.

• Schematic diagram of algorithm flow:

• Sorting of odd and even numbers:

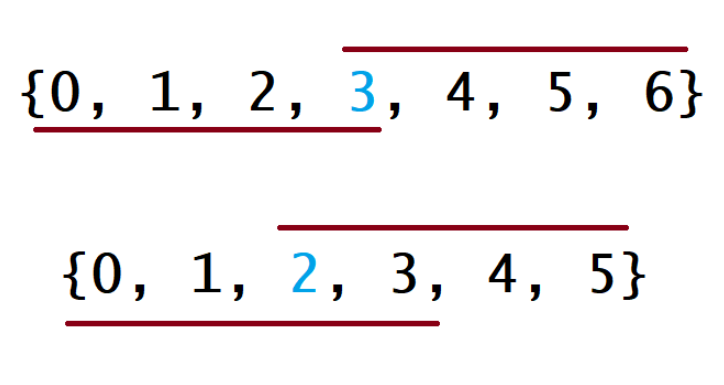
• In either case, the line below the array represents the subscript to be overwritten if the mode is the minimum value in the array, and the line below the array represents the subscript to be overwritten if the mode is the maximum value in the array. For other cases, this line will be in the middle of the two extreme cases. For these two extreme cases, they will overlap where the subscript is (n/2). Therefore, the value corresponding to the returned subscript (n/2) is correct regardless of the mode.

Code (python3)

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        nums.sort()
        res = nums[len(nums) // 2]
        return res
        #return nums[len(nums) // 2
        

Code (cpp)

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        return nums[nums.size() / 2];
    }
};

Complexity analysis:

• Time complexity: O(nlogn). The time complexity of sorting arrays is O(nlogn).
• Spatial complexity: O(logn). If you use the language's own sorting algorithm, you need to use O(logn) stack space. If you write your own heap sort, you only need to use the extra space of O(1).

Analytical idea 3: Moore voting

• Reference 1: Moore vote.

• Reference 2: K God analysis:.

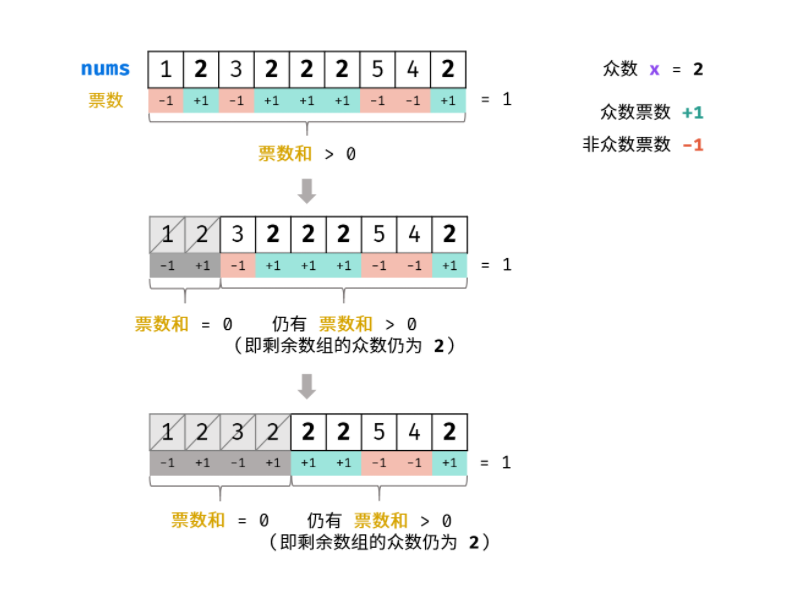
• Moore voting method, voting target value + +, not voting –, the core idea is that the number of votes is offset by positive and negative. More than half of the people vote, and the result is achieved

• Schematic diagram of algorithm flow:
  

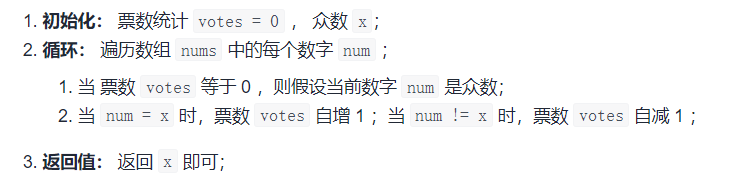
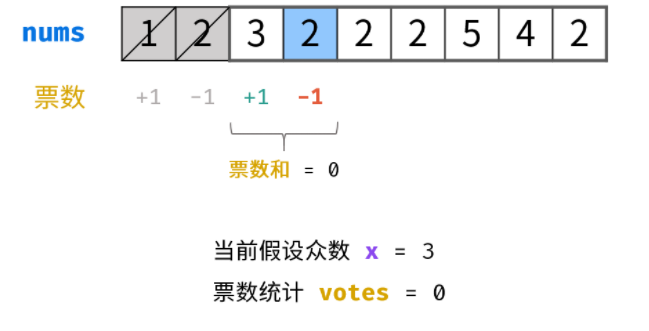
• Algorithm flow:

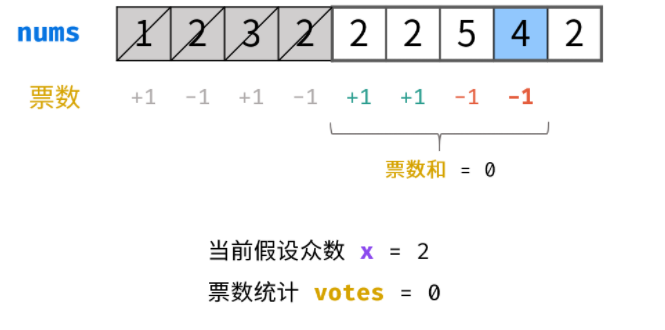
Code (python3)

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        count = 0
        candidate = None

        for num in nums:
            if count == 0:
                candidate = num
            count += (1 if num == candidate else -1)
        return candidate

• perhaps

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        votes = 0
        for num in nums:
            if votes == 0: x = num
            votes += 1 if num == x else -1
        return x

Code (cpp)

class Solution {
public:
    int majorityElement(vector<int>& nums) {    
//Moore voting method, vote for the target value + +, don't vote --, more than half of the people vote, and the result
        int count = 0, candidate = 0;
        for(int n : nums)
        {
            if(count == 0)        candidate = n;

            if(n == candidate)    count++;
            else                  count--;
        }
        return candidate;
    }
};

• perhaps

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int x = 0, votes = 0;
        for(int num : nums){
            if(votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        return x;
    }
};

• Complexity analysis:

• Time complexity: O(n). Moore algorithm only traverses the array once.

• Space complexity: O(1). Moore algorithm requires only constant level extra space.