Sword finger Offer 57 And two numbers with s - LeetCode (LeetCode CN. Com)
catalogue
Scheme 2: improvement of basic method
Option 4: from both sides to the middle
Case 1: x[i- θ 1] + x[j - θ 2] == target.
Case 2: x[i+ θ 1] + x[j + θ 2] == target
Scheme 1: basic method
thinking
First, put all the elements of the array into the hash table, and then traverse the hash table. For each element x, find out whether s-x is also in the hash table.
Complexity
The time complexity is O(N) and the space complexity is O(N)
code
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_set<int> iset(nums.begin(), nums.end());
for (auto x : iset) {
int y = target - x;
if (x != y && iset.find(y) != iset.end()) return {x, y};
}
return {};
}
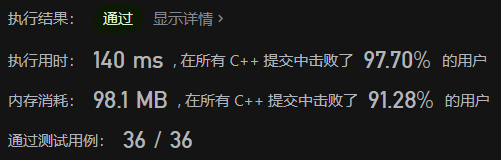
};Operation results
This scheme uses the unordered of STL_ Set, the time constant is relatively large. When the test case scale is relatively small, it does not show an advantage in performance.
Scheme 2: improvement of basic method
thinking
Traverse the array. For each element X of the array, first find out whether x is in the hash table. If x is not in the hash table, put s - x into the hash table; Until an X is found in the hash table.
Complexity
The time complexity is lower than O(N) and the space complexity is lower than O(N), both of which depend on the test case.
code
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int s) {
unordered_set<int> iset;
for (auto x : nums) {
int y = s - x;
if (y != x && iset.find(x) != iset.end()) return {x, y};
else iset.emplace(y);
}
return {};
}
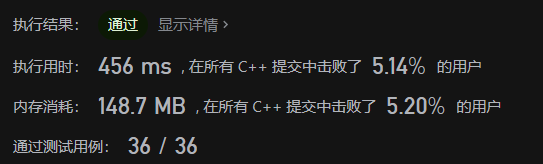
};Operation results

The same problem: the time constant of maintaining STL hash table is large, and it does not show performance advantage when the amount of data is small.
Scheme 3: binary search
thinking
Traversing the incremental sequence: x[1], x[2],..., x[n]. For a certain x[i], let y[i] = s - x[i]. If y[i] > x[n], proceed to the next; If y[i] < = x[n], find y[i] in x[i+1]~x[n].
Complexity
We can construct a sequence and a sum. Starting from the first element, we need to find it every time until the last. At this time, there is the worst time complexity: O (log2 (n) + log2 (n-1) +... + log2(1) = log2 (n!) )< O( n*log2(n) )
The space complexity is O(1)
code
class Solution {
public:
vector<int> twoSum(vector<int>& x, int s) {
vector<int> ans;
int N = x.size();
for (int i = 0; i != N; ++i) {
int y = s - x[i];
if (y <= x[N - 1]) {
int beg = i + 1, end = N;
while (beg != end) {
int mid = beg + (end - beg) / 2;
if (x[mid] == y) return { x[i], y };
x[mid] > y ? end = mid : beg = mid + 1;
}
}
//if (y <= x[N - 1] && Search(x, i + 1, N, y)) return { x[i], y };
}
return {};
}
/*
bool Search(vector<int>& x, int beg, int end, int target) {
while (beg != end) {
int mid = beg + (end - beg) / 2;
if (x[mid] == target) return true;
x[mid] > target ? end = mid : beg = mid + 1;
}
return false;
}
*/
};Operation results
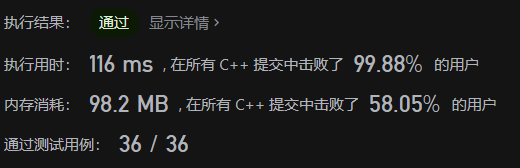
Option 4: from both sides to the middle
thinking
Sequence: x[1], x[2],..., x[n]. iter moves from front to back, riter , from back to front, and set s = x[i] + x[j]. If s < target, then the forward iterator moves backward, that is + + iter, otherwise the reverse iterator moves forward, that is -- riter, until s == target.
code
class Solution {
public:
vector<int> twoSum(vector<int>& x, int target) {
int i = 0, j = x.size() - 1;
while (i < j) {
int s = x[i] + x[j];
if (s == target) return { x[i], x[j] };
s < target ? ++i : --j;
}
return {};
}
};Proof of correctness
Direct proof
From iter = 1, riter = n, always keep ITER < riter
- If s (iter, riter) = x [iter] + x [riter] < target, all these sums from s(iter, iter+1) to s(iter, riter-1) are less than target, so they can be excluded - + + iter
- If s (ITER, riter) = x [ITER] + x [riter] > target, all these sums from s(iter + 1, riter) to s(riter-1, riter) are greater than target, so they can be excluded - - riter
Therefore, we can ensure that from the first step, the wrong answers are excluded in each step. The process of completing is actually the process of eliminating all wrong answers; Because every step is correct, the whole process is correct.
Counter evidence method
Suppose i and j are currently in progress. If you want to miss the correct answer, there can only be two situations:
-
Case 1: x[i- θ 1] + x[j - θ 2] == target.
At this point: x [i] > x [i]- θ 1],x[j] > x[j - θ 2] x[i] + x[j] > target
Because i can only increase but not decrease, i miss the correct answer.
Analysis 1
Before the forward iterator iter reaches I, it must pass through I- θ 1. At this time, the reverse iterator riter is in j- θ After 2, x [riter] > x [j- θ 2] , then x[i- θ 1] + x [riter] > target. According to the rule, the reverse iterator should move forward at this time, that is -- riter. The forward iterator iter cannot reach I.
-
Case 2: x[i+ θ 1] + x[j + θ 2] == target
At this time, x [i] < x [i]+ θ 1],x[j] < x[j + θ 2] x[i] + x[j] < target
Because j can only decrease, not increase, so I miss the correct answer.
Analysis 2
Before the reverse iterator riter reaches j, it must pass through j+ θ 2. At this time, the forward iterator iter is at i+ θ Before 1, x [iter] < x [i+ θ 1] , then x[iter] + x[j+ θ 2] < target, according to the rule, the forward iterator should be moved backward, that is + + iter, and the reverse iterator riter cannot reach j.
Complexity
Time complexity O(N), space complexity O(1).
Operation results