"Leetcode : https://leetcode-cn.com/problems/nge-tou-zi-de-dian-shu-lcof

"GitHub : https://github.com/nateshao/leetcode/blob/main/algo-notes/src/main/java/com/nateshao/sword_offer/topic_47_dicesProbability/Solution.java

Sword finger offer 60 Points of N dice

"Title Description: throw n dice on the ground, and the sum of the points on the upward side of all dice is s. enter N and print out the probability of all possible values of S. You need to return the answer with an array of floating-point numbers, in which the i-th element represents the probability of the i-th smallest in the set of points that the n dice can roll.

Difficulty: medium

Example 1:

input: 1
 output: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]

Example 2:

input: 2
 output: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]

Method 1: Violence Law

Given n dice, you can get:

• The probability of each dice shaking to 1 to 6 is equal, which is 1 / 6
• Regarding the points of each dice as an independent case, there are 6n "point combinations". For example, when n = 2, the combination of points is: (1,1), (1,2), (2, 1),(2,2),，.. , (6,1),... , (6,6)
• The range of "sum of points" of N dice is [n, 6n], and the number is 6n-n+1=5n+ 1. Violence statistics: each "point combination" corresponds to a "point sum". Consider traversing all point combinations, count the number of occurrences of each point sum, and finally divide it by the total number of point combinations (i.e. divide by 6N), that is, get the occurrence probability of each point sum.

"As shown in the figure below, it is the calculation process of point combination, point sum and probability of each point when n=2 is input.

The violence method needs to traverse all combinations of points, so the time complexity is O(6^n). Observe that the input value range of this question is 1 ≤ n ≤ 11

Method 2: dynamic programming

Let the solution of N dice (i.e. probability list) be f(n), where the probability of "point sum" x is f(n, x).

Assuming that the solution f (n-1) of n-1 dice is known, add a dice and find the probability f(n, x) that the sum of the points of N dice is X. when the number of dice added is 1, the sum of the points of the first n-1 dice should be X-1, which can form points and X; Similarly, when this die is 2, the first n-1 dice should be x- 2; And so on until the number of dice is 6. The probability f(n. x) can be obtained by adding the probabilities of these six cases. The recurrence formula is as follows:

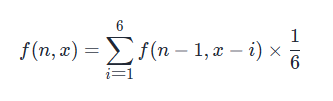
According to the above analysis, it is known that f(n) can be recursively calculated through the solution f(n- 1) of the subproblem, and the solution f(1) of inputting a dice is known, so any solution f(n) can be recursively derived through the solution f(1). As shown in the figure below, it is a recursive calculation example of n = 2 and x = 7.

It is found that although the above recursive formula is feasible, X-i in F (n-1, X-i) will cross the boundary. For example, if you want to recursively calculate f(2,2), because the number and range of a dice is [1,6], you should only sum f(1,1), that is, f(1,0), f (1, - 1) F (1, - 4) is meaningless. This cross-border problem makes it more difficult to write code.

"As shown in the figure below, the above recurrence formula is" reverse ", that is, in order to calculate f(n,x), sum all relevant situations; If we change it to the "positive" recursive formula, we can solve the cross-border problem.

Specifically, since the number of new dice can only be 1 to 6, the probability f(n-1,x) is only related to f (n, x + 1), f (n, x + 2) F (n, x + 6) correlation. However, by traversing the probability of the sum of points in F (n-1) and adding it to all relevant terms in f(n), the recurrence from F (n-1) to f(n) can be completed.

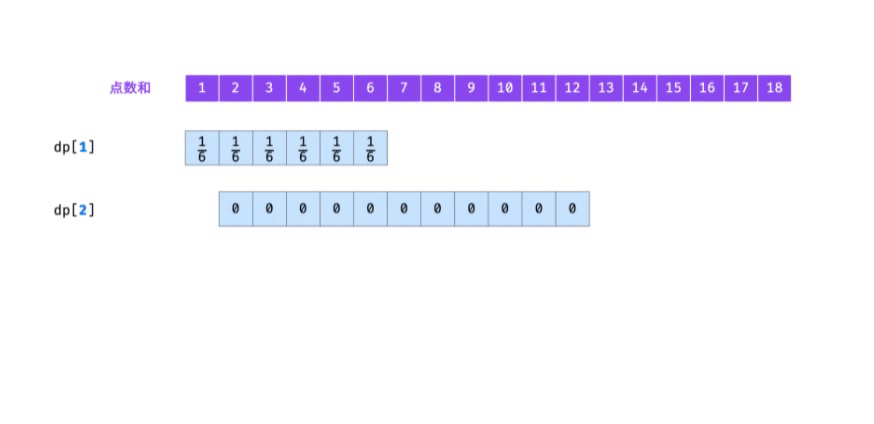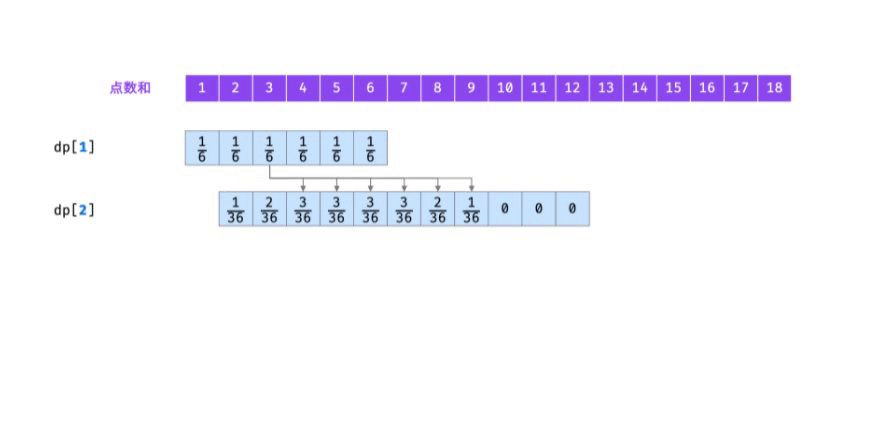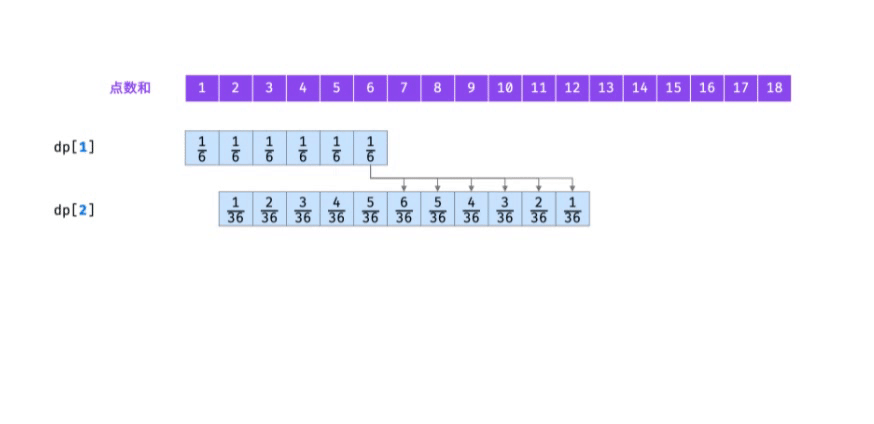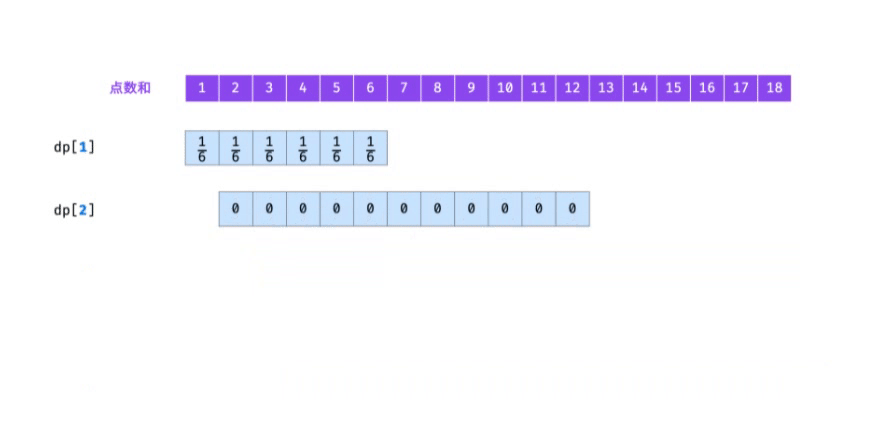
"If f(i) is recorded as a dynamic programming list dp[i, the state transition process of I = 1, 2,... N is shown in the figure below.

Complexity analysis:

• Time complexity O(n^2)
• Spatial complexity O(n)

Code: the usual practice is to declare a two-dimensional array dp, dp[i] [j] represents the number of points of the first I dice and the probability of j, and perform state transition. dp[i] is only recursively derived from dp[i-1]. In order to reduce the spatial complexity, only two one-dimensional arrays dp and TMP can be established alternately.

public double[] dicesProbability(int n) {
        //Because the final result is only related to the previous dynamic transfer array, only one-dimensional dynamic transfer array needs to be set here
        //Originally, dp[i][j] represents the probability that the sum of the points of the first I dice is j. now only the array of the last state is needed, so only one-dimensional array dp[j] represents the probability of each result under n dice.
        //The initial is the sum of points in the case of one dice, and there are only 6 results, so the size initialized with dp is 6
        double[] dp = new double[6];
        //There is only one array
        Arrays.fill(dp,1.0/6.0);
        //Start with the second dice, where n means n dice. First calculate from the second case, and then gradually find 3, 4... N cases
        //i represents the result when there are a total of i dice
        for(int i=2;i<=n;i++){
        //The sum range of points will change a little each time. The maximum value of the sum of points is i*6 and the minimum value is i*1. The result value before i will not appear;
        //For example, when i=3 dice, the minimum is 3, which cannot be 2 and 1. Therefore, the number of the sum of points is 6*i-(i-1). Simplification: 5*i+1
            //When there are i dice, the value array of the sum of points is assumed to be temp
            double[] temp = new double[5*i+1];
            //Starting with the value array of the sum of points of i-1 dice, calculate the value of the sum of points array of i dice
            //First take the j-th value of the sum of points of i-1 dice, which affects the value of temp[j+k] when i dice
            for(int j=0;j<dp.length;j++){
            //For example, when there is only one dice, dp[1] represents the probability when the sum of dice points is 2, which will have an impact on the sum of points when there are two dice is 3, 4, 5, 6, 7 and 8, because when the value of one dice is 2, the value of the other dice can be 1 ~ 6, and the sum of points generated is 3 ~ 8; For example, dp[2] represents that the sum of points is 3, which will have an impact on the sum of points when there are two dice: 4, 5, 6, 7, 8 and 9; Therefore, K here corresponds to six situations that may occur when the i-th dice appear. It's easy to understand a lot by drawing a dynamic programming backstepping diagram like k God
                for(int k=0;k<6;k++){
                    //Remember here is to add the product of dp array value and 1 / 6. 1 / 6 is the probability of the i-th dice rolling a certain value
                    temp[j+k]+=dp[j]*(1.0/6.0);
                }
            }
            //After the sum of the points of i dice is calculated, the temp array should be handed over to the dp array, which will represent the probability of the sum of the possible points of i dice; Used to calculate the probability of the sum of points when i+1 dice
            dp = temp;
        }
        return dp;
    } 

Reference link: https://leetcode-cn.com/problems/nge-tou-zi-de-dian-shu-lcof/solution/jian-zhi-offer-60-n-ge-tou-zi-de-dian-sh-z36d

END