Sword finger Offer notes [Python description]
Find in 2D array
Title Description:
In a two-dimensional array (each one-dimensional array has the same length), each row is sorted in ascending order from left to right, and each column is sorted in ascending order from top to bottom. Please complete a function, enter such a two-dimensional array and an integer, and judge whether the array contains the integer.
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
Given target = 7, return true.
Given target = 3, false is returned.
Data range: the length and width of the matrix meet \ (0 \leq n, m \leq 500 \), and the values in the matrix meet \ (0 \leq v a l \leq 10^{9} \) advanced: space complexity \ (O(1) \), time complexity \ (O(n+m) \)
Enter Description:
7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
Output Description:
true
The code is as follows:
def find(target, array):
i = 0
j = len(array[0]) - 1
while i < len(array) and j >= 0:
base = array[i][j]
if target == base:
return True
elif target > base:
i += 1
else:
j -= 1
return False
print(find(4,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]))
Replace spaces
Title Description:
Please implement a function to replace each space in a string s with "% 20".
For example, when the string is We Are Happy Then the replaced string is We%20Are%20Happy.
Data range: \ (0 \leq \operatorname{len}(s) \leq 1000 \). Ensure that the characters in the string are one of uppercase English letters, lowercase English letters and spaces. Advanced: time complexity \ (O(n) \), space complexity \ (O(n) \)
Enter Description:
"We Are Happy" " "
Output Description:
"We%20Are%20Happy" "%20"
The code is as follows:
def replaceSpace(s):
# write code here
s_len = len(s)
space_count = 0
for i in s:
if i == ' ':
space_count += 1
s_len += 2 * space_count
new_array = [' '] * s_len
j = 0
for i in range(len(s)):
if s[i] == ' ':
new_array[j] = '%'
new_array[j+1] = '2'
new_array[j+2] = '0'
j += 3
else:
new_array[j] = s[i]
j += 1
return ''.join(new_array)
print(replaceSpace('We Are Happy'))
Print linked list from end to end
Title Description:
Enter the head node of a linked list and return the value of each node in the order from the end to the head of the linked list (returned with an array).
For example, the linked list of {1,2,3} is as follows:

Returns an array of [3,2,1]
0 < = linked list length < = 10000
Enter Description:
{67,0,24,58}
Output Description:
[58,24,0,67]
The code is as follows:
class ListNode(object):
def __init__(self, x):
self.val = x
self.next = None
# Solution 1: store with auxiliary stack
def printListFromTailToHead(listNode):
# write code here
stack = []
result_array = []
node_p = listNode
while node_p:
stack.append(node_p.val)
node_p = node_p.next
while stack:
result_array.append(stack.pop(-1))
return result_array
# Solution 2: self stack call
result_array = []
def printListFromTailToHead(listNode):
# write code here
if listNode:
printListFromTailToHead(listNode.next)
result_array.append(listNode.val)
return result_array
Rebuild binary tree
Title Description:
Given the preorder traversal and inorder traversal results of a binary tree with n nodes, please reconstruct the binary tree and return its head node.
For example, enter the preorder traversal sequence {1,2,4,7,3,5,6,8} and the middle order traversal sequence {4,7,2,1,5,3,8,6}, and the reconstruction is shown in the following figure.
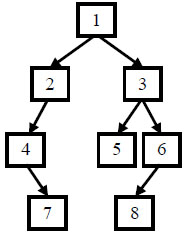
Tips:
1.vin.length == pre.length
2. There are no duplicate elements in pre and vin
3. All elements in VIN appear in pre
4. Just return to the root node, and the system will automatically output the whole tree for answer comparison
Data range: \ (n \leq 2000 \), node value \ (- 10000 \leq\) val \(\leq 10000 \) requirements: space complexity \ (O(n) \), time complexity \ (O(n) \)
Enter Description:
[1,2,4,7,3,5,6,8],[4,7,2,1,5,3,8,6]
Output Description:
{1,2,3,4,#,5,6,#,7,#,#,8}
explain:
Return to the root node, and the system will output the comparison result of the whole binary tree. The reconstruction result is shown in the figure below
The code is as follows:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
# Returns the root node of the constructed TreeNode
def reConstructBinaryTree(pre, tin):
# write code here
if not pre:
return None
root_val = pre[0]
root = TreeNode(root_val)
for i in range(len(tin)):
if tin[i] == root_val:
break
root.left = reConstructBinaryTree(pre[1:1+i], tin[:i])
root.right = reConstructBinaryTree(pre[1+i:], tin[i+1:])
return root
def preorder(root):
if root:
preorder(root.left)
print(root.val)
preorder(root.right)
preorder(reConstructBinaryTree([1,2,3,4,5,6,7],[3,2,4,1,6,5,7]))
Queue with two stacks
Title Description:
Two stacks are used to implement a queue, and n elements are used to complete the functions of inserting integers (push) at the end of the queue n times and deleting integers (pop) at the head of the queue n times. The element in the queue is of type int. Ensure that the operation is legal, that is, ensure that there are elements in the queue during pop operation.
Data range: \ (n \leq 1000 \) requirements: the space complexity of storing \ (n \) meta bindings is \ (O(n) \), and the time complexity of "entering" and "deleting" is \ (O(1) \)
Enter Description:
["PSH1","PSH2","POP","POP"]
Output Description:
1,2 explain: "PSH1":Represents inserting 1 at the end of the queue "PSH2":Represents inserting 2 at the end of the queue "POP":Represents deleting an element, first in first out=>Return 1 "POP":Represents deleting an element, first in first out=>Return 2
The code is as follows:
class CQueue(object):
def __init__(self):
self.stack1 = []
self.stack2 = []
def appendTail(self, value):
self.stack1.append(value)
def deleteHead(self):
if not self.stack2:
while self.stack1:
self.stack2.append(self.stack1.pop(-1))
if len(self.stack2) == 0:
return -1
return self.stack2.pop(-1)
- thinking
A stack is used to store. Stack2 pops up when pop, stack2 is empty, and stack1 is stored in stack2 when pop.
Minimum number of rotation array
Title Description:
There is a non descending array with length n, such as [1,2,3,4,5]. Rotate it, that is, move the first elements of an array to the end of the array to become a rotating array, such as [3,4,5,1,2], or [4,5,1,2,3]. Excuse me, given such a rotation array, find the minimum value in the array.
Data range: \ (1 \leq n \leq 10000 \), value of any element in the array: \ (0 \leq\) val \(\leq 10000 \) requirements: space complexity: \ (O(1) \), time complexity: \ (O(\operatorname{logn}) \)
Enter Description:
[3,4,5,1,2]
Output Description:
1
The code is as follows:
class Solution(object):
def minArray(self, numbers):
low, high = 0, len(numbers) - 1
while low < high:
mid = (high+low) / 2
if numbers[mid] > numbers[high]:
low = mid + 1
elif numbers[mid] < numbers[high]:
high = mid
else:
if (numbers[high - 1] > numbers[high]): # Ensure correct subscript
low = high
break
high -= 1 # If numbers [high-1] = numbers [high]
return numbers[low]
thinking
Overall dichotomy:
- if mid is greater than high, low = mid - 1
- if mid is less than high, high = mid
- Until mid=high, take the number at this position
Fibonacci sequence
Title Description:
We all know the Fibonacci sequence. Now it is required to enter a positive integer \ (n \), please output the \ (n \) item of the Fibonacci sequence. The jujubonacci sequence is one that satisfies \ (f I B (x) = \ left \ {\ begin {array} {RC} 1 & x = 1,2 \ \ f I B (x-1) + F I B (X-2) & x > 2 \ end {array} \ right. \)
- Data range: \ (1 \leq n \leq 39 \)
- Requirements: space complexity \ (O(1) \), time complexity \ (O(n) \), and this problem also has the solution of time complexity \ (O(\operatorname{logn}) \)
Enter Description:
A positive integer n 4
Output Description:
Output a positive integer. 3 According to the definition of Fibonacci sequence, fib(1)=1,fib(2)=1,fib(3)=fib(3-1)+fib(3-2)=2,fib(4)=fib(4-1)+fib(4-2)=3,So the answer is 4.
The code is as follows:
def Fibonacci(n):
# write code here
f1 = 0
f2 = 1
if n == 0: return f1
elif n == 1: return f2
for _ in range(n-1):
f2, f1 = f1+f2, f2
return f2
print(Fibonacci(3))
Jump steps
Title Description:
A frog can jump up one step or two steps at a time. Find out the total number of jumping methods for the frog to jump up an n-step step (different results are calculated in different order).
Data range: \ (0 \leq n \leq 40 \)
Requirements: time complexity: \ (O(n) \), space complexity: \ (O(1) \)
Enter Description:
2
Output Description:
2 explain: There are two ways for frogs to jump up two steps: jump one step first, then one step, or directly jump two steps. So the answer is 2
The code is as follows:
class Solution(object):
def numWays(self, n):
if n == 0: return 1
f1 = 1
f2 = 2
if n == 1: return f1
if n == 2: return f2
for _ in range(n-2):
f2, f1 = f1+f2, f2
return f2 % 1000000007
thinking
Suppose there are f(n) jump methods for the nth step
Then f(n) = f(n-1) + f(n-2), where f (1) = 1 and f (2) = 2
Step jump expansion problem
Title Description:
A frog can jump up 1 step or 2 steps at a time... It can also jump up n steps. Find the total number of jumping methods for the frog to jump up an n-level step (n is a positive integer).
Data range: \ (1 \leq n \leq 20 \)
Advanced: space complexity \ (O(1), \) time complexity \ (O(1) \)
Enter Description:
3
Output Description:
4
The code is as follows:
def jumpFloorII(number):
# write code here
f1 = 1
if number == 1: return f1
for _ in range(number-1):
f1 = 2*f1
return f1
thinking
f(1)=1, f(2)=2, f(3)=4, f(4)=8 let n+1 level f(n+1), there are
f(n+1) = f(1) + f(2) + ... + f(n)
f(n+2) = f(1) + f(2) + ... + f(n+1)
f(n+2)= 2f(1) + 2f(2) + ... + 2f(n)
Therefore, f(n+2) = 2f(n+1)
Rectangular overlay
Title Description:
We can use the small rectangle of 21 to cover the larger rectangle horizontally or vertically. How many different methods are there to cover a 2*n large rectangle with n 21 small rectangles without overlap from the same direction?
Data range: \ (0 \leq n \leq 38 \)
Advanced: space complexity \ (O(1) \), time complexity \ (O(n) \)
Note: when the Convention n == 0, 0 is output
For example, when n=3, 2 * 3 rectangular blocks have three different covering methods (from the same direction):
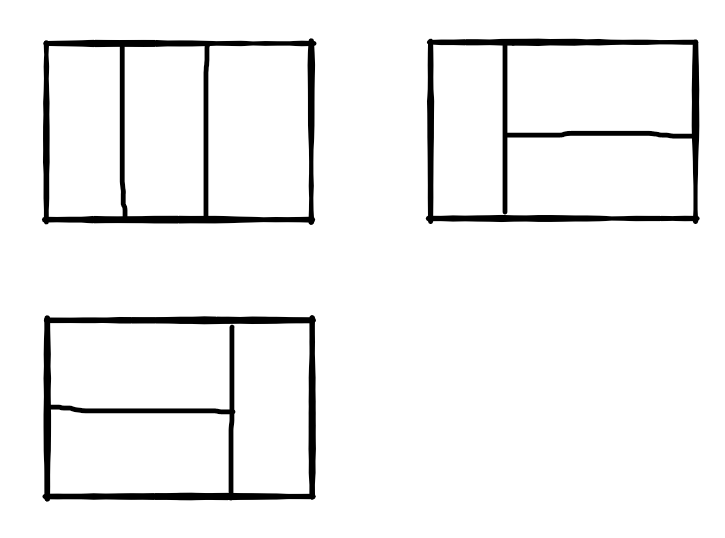
Enter Description:
//Total number of small rectangles of 2 * 1 n 4
Output Description:
5
The code is as follows:
def rectCover(number):
# write code here
f1 = 1
f2 = 2
if number == 1: return f1
if number == 2: return f2
for _ in range(number-2):
f2, f1 = f1 + f2, f2
return f2
print(rectCover(3))
thinking
f(1) = 1
f(2) = 2
f(n) = f(n-1) + f(n-2)
Number of 1 in binary
Title Description:
Enter an integer n and output the number of 1 in the 32-bit binary representation. Where negative numbers are represented by complements.
Data range: \ (- 2 ^ {31} < = n < = 2 ^ {31} - 1 \)
That is, the range is: \ (- 2147483648 < = n < = 2147483647 \)
Enter Description:
10 -1
Output Description:
2 32 explain: 1. The 32-bit binary representation of 10 in the decimal system is 0000 0000 0000 0000 1010, with two 1s. 2. Negative numbers are represented by complements,-1 The 32-bit binary representation of is 1111 1111 1111 1111 1111 1111 1111 1111, of which 32 are 1
The code is as follows:
def Power(base, exponent):
# write code here
if exponent == 0: return 1
flag = 1
if exponent < 0:
exponent *= -1
flag = 0
temp = base
res = 1
while(exponent):
if exponent & 1:
res *= temp
temp *= temp
exponent = exponent >> 1
return res if flag else 1.0/res
print(Power(2, 1))
thinking
If n= There is at least one 1 in the binary of 0, n
- If 1 is in the lowest order, the number n-1 & n just changes this 1 to 0.
- If 1 is not in the lowest order, the number n-1 & n just changes this 1 to 0.
Therefore, we can judge how many 1s there are in the binary system by judging the number of times n-1 & n can run circularly.
You need to use C in python_ Int() function, otherwise the negative number will not become 0.
Integer power of value
Title Description:
Implement the function double Power(double base, int exponent) to find the exponent power of the base.
Data range: \ (\ mid\) base \(|\leq 100,\), exponent \(\mid \leq 100 \), ensuring that the final result must meet \ (| v a l| \leq 10^{4} \) advanced: space complexity \ (O(1) \), time complexity \ (O(n) \)
Enter Description:
2.00000,-2
Output Description:
0.25000 2 of-2 The power is equal to 1/4=0.25
The code is as follows:
from ctypes import *
def NumberOf1(n):
# write code here
cnt = 0
while c_int(n).value:
n = n & (n-1)
cnt += 1
print(c_int(n), n)
return cnt
print(NumberOf1(-3))
Adjust the array order so that odd numbers precede even numbers (one)
Title Description:
Enter an array of integers with a length of n, and the array does not contain the same elements. Implement a function to adjust the order of numbers in the array, so that all odd numbers are in the front part of the array and all even numbers are in the back part of the array, and ensure that the relative positions between odd numbers and odd numbers, even numbers and even numbers remain unchanged.
Data range: \ (0 \leq n \leq 5000 \), value of each number in the array \ (0 \leq\) val \(\leq 10000 \)
Requirements: time complexity \ (O(n) \), space complexity \ (O(n) \)
Advanced: time complexity \ (O\left(n^{2}\right) \), space complexity \ (O(1) \)
Enter Description:
[2,4,6,5,7]
Output Description:
[5,7,2,4,6]
The code is as follows:
def reOrderArray(array):
# write code here
odd_cnt = 0
res = [0] * len(array)
# Number of Statistics
for n in array:
if n % 2 != 0:
odd_cnt += 1
# Pit filling
odd_i = 0
even_i = odd_cnt
for i in range(len(array)):
if array[i] % 2 != 0:
res[odd_i] = array[i]
odd_i += 1
else:
res[even_i] = array[i]
even_i += 1
return res
The penultimate k nodes in the linked list
Title Description:
Enter a linked list with a length of n, set the value of the element in the linked list as ai, and return the penultimate node in the linked list.
If the length of the linked list is less than k, please return a linked list with a length of 0.
Data range: \ (0 \leq n \leq 10^{5}, 0 \leq a_{i} \leq 10^{9}, 0 \leq k \leq 10^{9} \)
Requirements: space complexity \ (O(n) \), time complexity \ (O(n) \)
Advanced: space complexity \ (O(1) \), time complexity \ (O(n) \)
For example, when {1,2,3,4,5}, 2 is entered, the corresponding linked list structure is shown in the following figure:
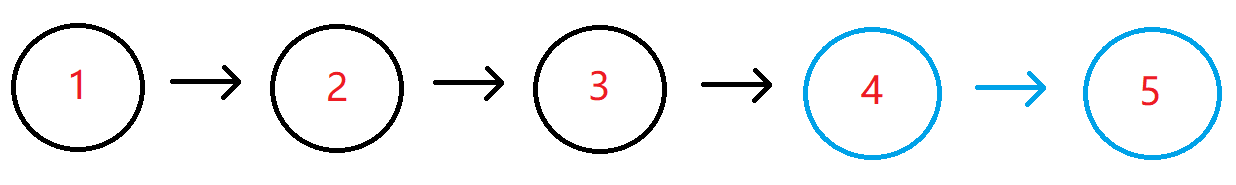
The blue part is the last two nodes of the linked list, so the penultimate node (that is, the node with node value of 4) can be returned. The system will print all the following nodes for comparison.
Enter Description:
{1,2,3,4,5},2
Output Description:
{4,5}
explain:
Return the penultimate node 4, and the system will print all the following nodes for comparison.
The code is as follows:
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def FindKthToTail(head, k):
# write code here
if not head: return None
fast_p = head
slow_p = head
for _ in range(k):
if fast_p:
fast_p = fast_p.next
else:
return None
while fast_p:
fast_p = fast_p.next
slow_p = slow_p.next
return slow_p
thinking
Use the fast and slow pointer. The fast pointer is k steps faster than the slow pointer. When you reach the tail node, the slow pointer is the penultimate node.
Reverse linked list
Title Description:
Given the head node phead of a single linked list (the head node has a value, for example, in the figure below, its val is 1) and the length is n, after reversing the linked list, return the header of the new linked list.
Data range: \ (n \leq 1000 \) requirements: space complexity \ (O(1) \), time complexity \ (O(n) \)
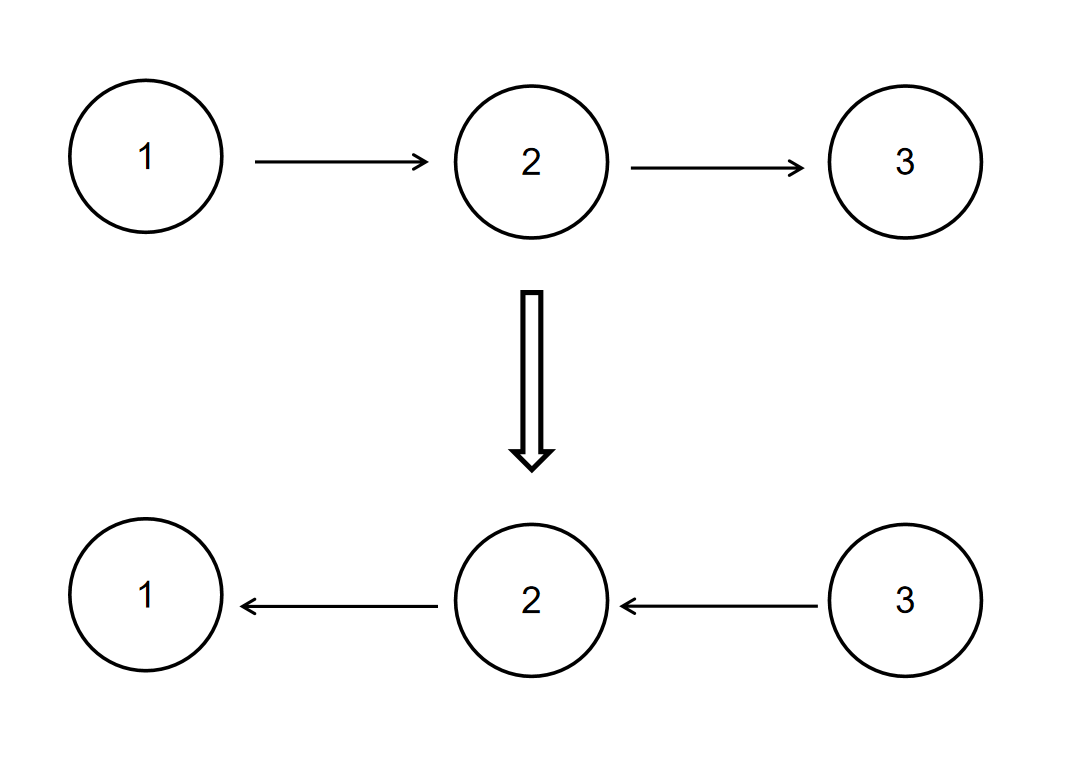
For example, when the linked list {1,2,3} is entered,
After inversion, the original linked list becomes {3,2,1}, so the corresponding output is {3,2,1}.
The above conversion process is shown in the figure below:
Enter Description:
{1,2,3}
Output Description:
{3,2,1}
The code is as follows:
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def ReverseList(pHead):
# write code here
if not pHead: return None
head = ListNode(0)
head.next = pHead
p = pHead
while(p.next):
tp = p.next
p.next = p.next.next
tp.next = head.next
head.next = tp
return head.next
thinking
Suppose to flip 1 - > 2 - > 3 - > 4 - > 5, the steps are as follows:
head->4->3->2->1->5
p tp
- 1. We point the next of p to the next of tp
- 2. Point tp's next to head's next
- 3. Point the next of head to tp
Merge ordered linked list
Title Description:
Enter two incremental linked lists. The length of a single linked list is \ (n \), merge the two linked lists and make the nodes in the new linked list still be sorted incrementally.
Data range: \ (0 \leq n \leq 1000, - 1000 \leq {\text {node value} \ leq 1000} {} \)
Requirements: space complexity \ (O(1), \) time complexity \ (O(n) \)
For example, when {1,3,5} and {2,4,6} are input, the combined linked list is {1,2,3,4,5,6}, so the corresponding output is {1,2,3,4,5,6}. The conversion process is shown in the following figure:
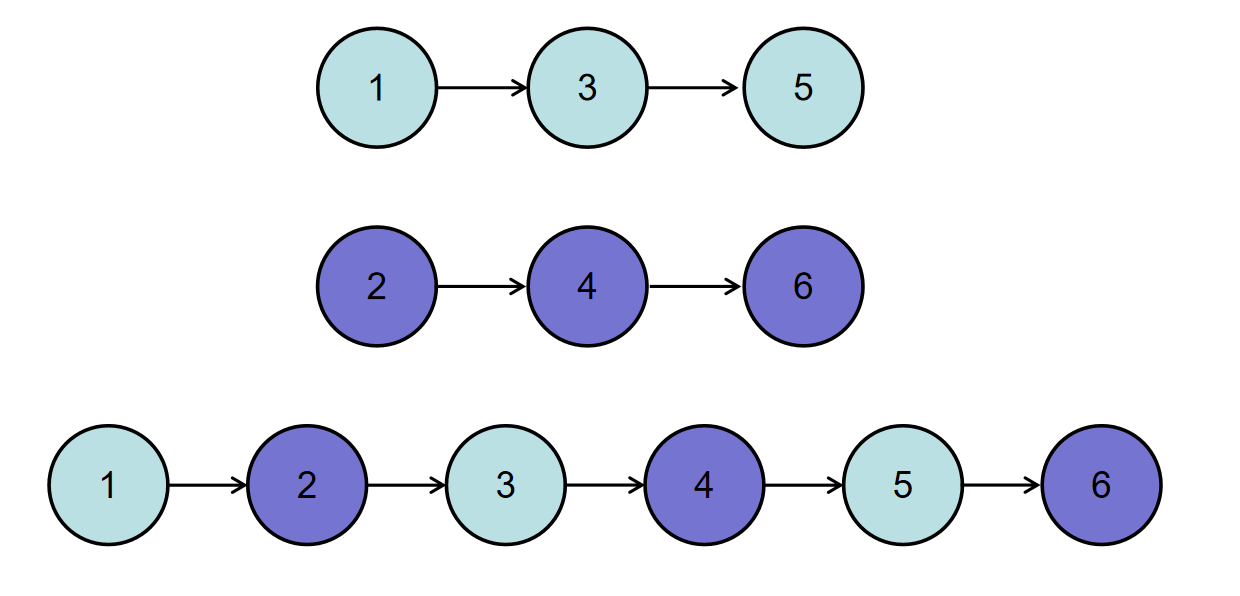
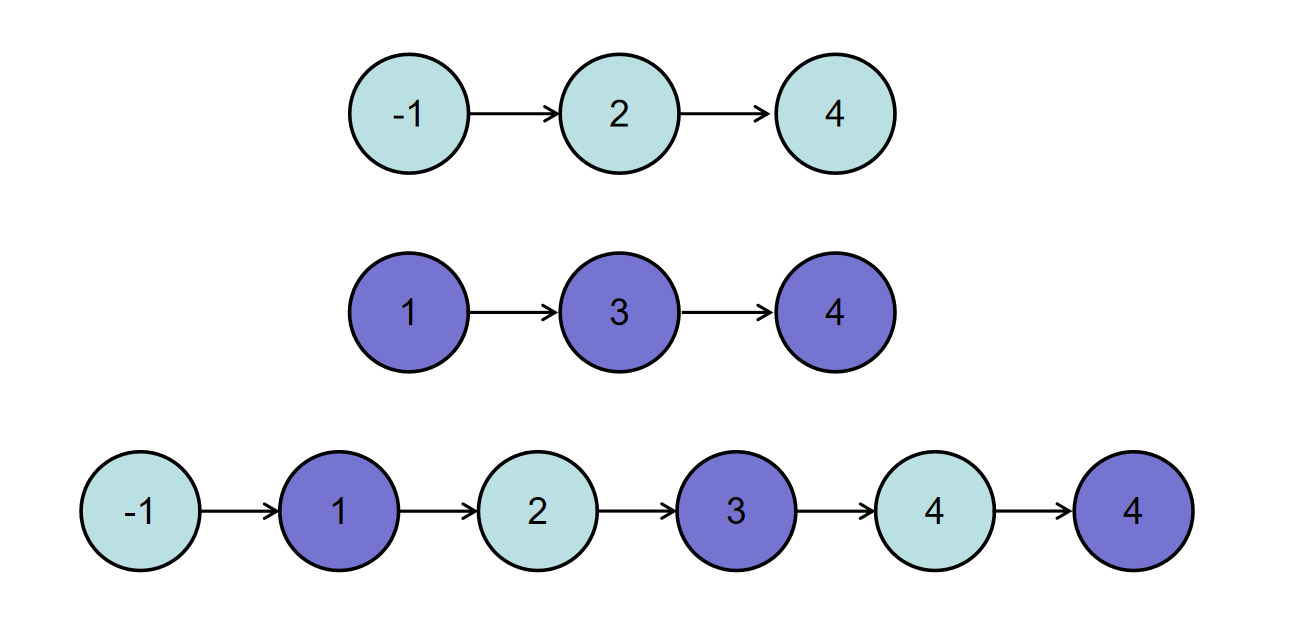
Or input {- 1,2,4}, {1,3,4}, the combined linked list is {- 1,1,2,3,4,4}, so the corresponding output is {- 1,1,2,3,4,4}. The conversion process is shown in the following figure:
Enter Description:
{-1,2,4},{1,3,4}
Output Description:
{-1,1,2,3,4,4}
The code is as follows:
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def Merge(pHead1, pHead2):
# write code here
res = ListNode(0)
head = res
while pHead1 and pHead2:
if pHead1.val <= pHead2.val:
head.next = pHead1
head = head.next
pHead1 = pHead1.next
else:
head.next = pHead2
head = head.next
pHead2 = pHead2.next
if pHead1:
head.next = pHead1
if pHead2:
head.next = pHead2
return res.next
Substructure of tree
Title Description:
Input two binary trees a and B to judge whether B is the substructure of A. (we agree that an empty tree is not a substructure of any tree)
If a is {8,8,7,9,2, #, #, #, #, #, 4,7}, and B is {8,9,2}, the structure of the two trees is as follows. It can be seen that B is the substructure of A
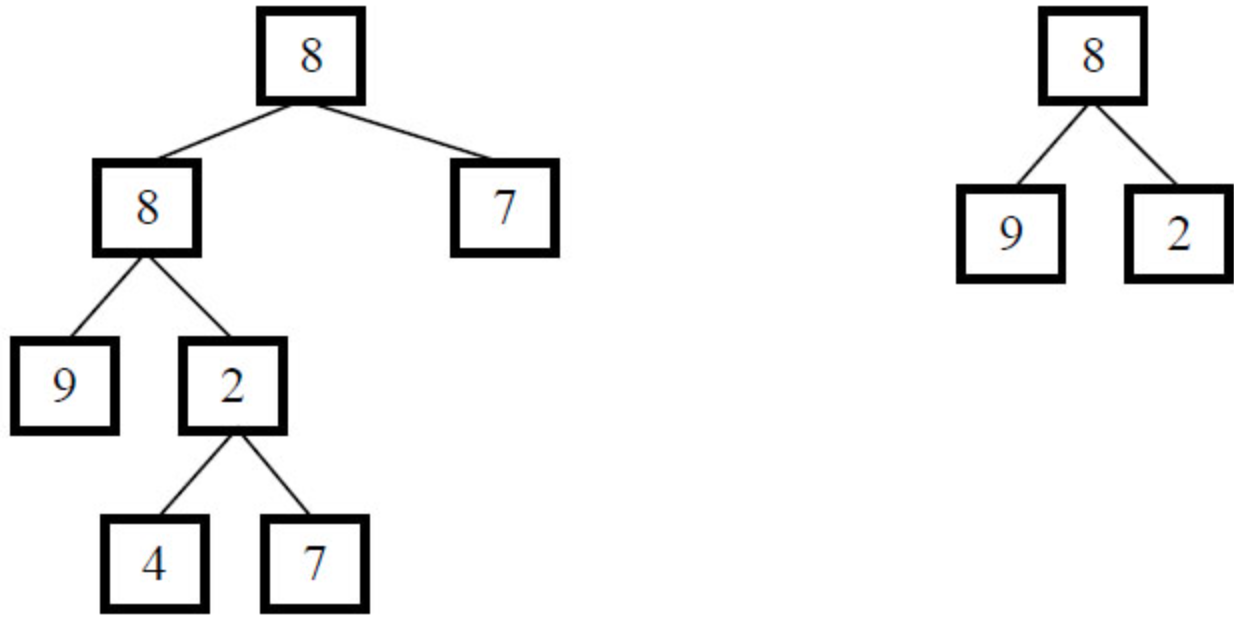
Data range:
0 < = number of nodes of a < = 10000
0 < = number of nodes of B < = 10000
Enter Description:
{8,8,7,9,2,#,#,#,#,4,7},{8,9,2}
Output Description:
true
The code is as follows:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def helper(treeA, treeB):
if not treeB:
return True
elif not treeA:
return False
elif treeA.val != treeB.val:
return False
else:
return helper(treeA.left, treeB.left) and helper(treeA.right, treeB.right)
def HasSubtree(pRoot1, pRoot2):
# write code here
if not pRoot1 or not pRoot2: return False
# Is 2 a subtree of 1
res = False
if pRoot1.val == pRoot2.val:
res = helper(pRoot1, pRoot2)
if res:
return True
else:
return HasSubtree(pRoot1.left, pRoot2) or HasSubtree(pRoot1.right, pRoot2)
thinking
-
- Traverse parent structure
-
- Determine whether the substructures are the same