First level binary tree traversal

Topic introduction

Given a (pre order traversal) string, construct a binary tree and print it in medium order, # = = nullpet, '' = = empty tree

If you forget, please read this blog ----- > Review the concept of binary tree

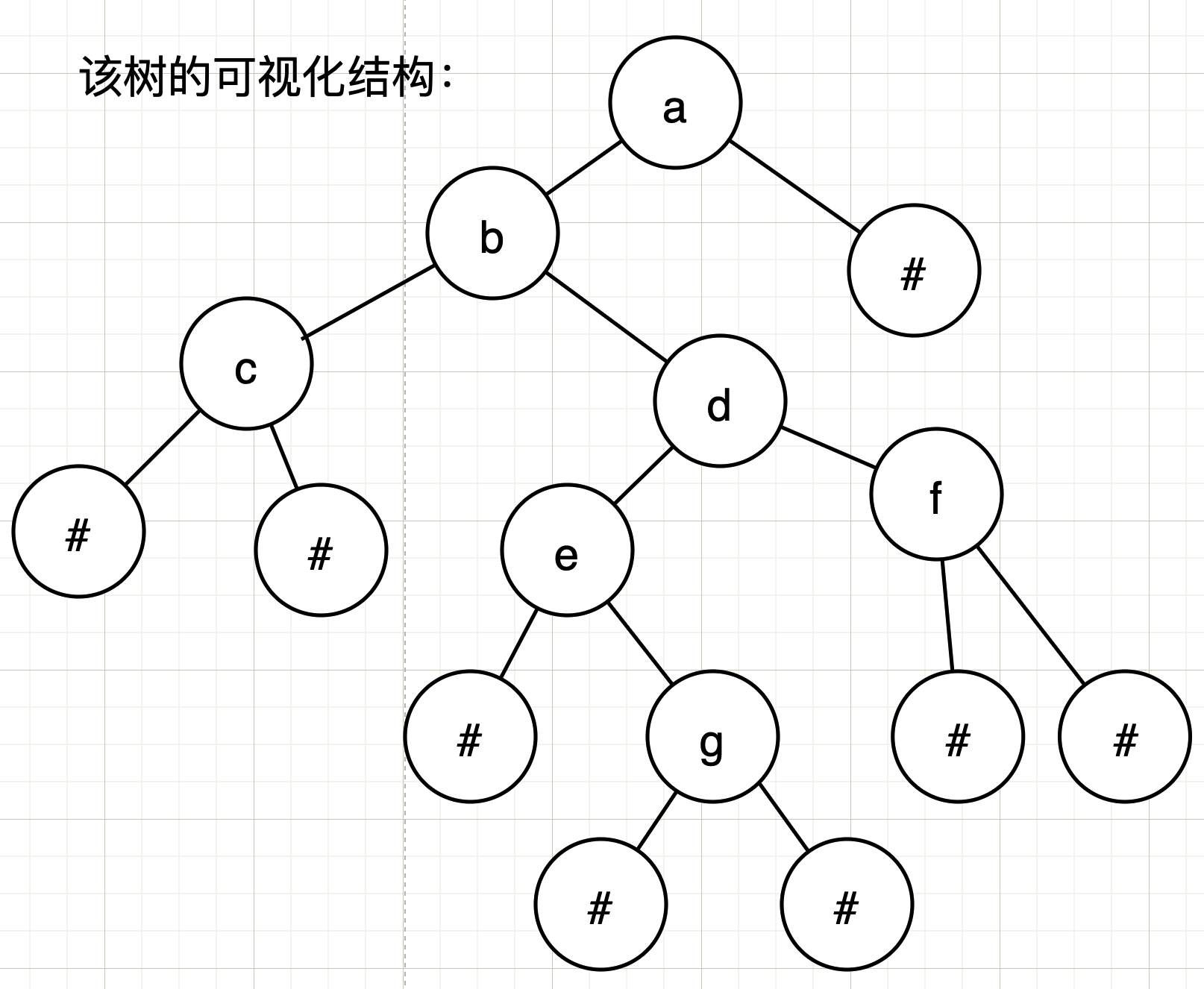
thinking

1. Preorder is first root traversal, in the left subtree and right subtree
2. The left and right intervals of the tree are constructed respectively
3. Build the tree according to # the following two situations:

One # indicates that the current construction interval has been completed and no elements can be constructed (similar to the middle order traversal to the leaf node)
If you encounter ## a leaf node, it means that the left and right intervals are built (the subsequent traversal goes all the way to the root node)

code:

#include<iostream>
using namespace std;
struct TreeNode 
{
      char val;
      TreeNode *left;
      TreeNode *right;
      TreeNode(char x) : val(x), left(NULL), right(NULL) {}
  };

TreeNode*Construction(string &d1,int& i)
{
    if(d1[i]=='#'/ / half subtree has been built
    {
        return nullptr;
    }
    TreeNode *root=new TreeNode(d1[i]);//Construction node
    
    root->left=Construction(d1,++i);//Construct left subtree
    root->right=Construction(d1,++i);//Construct right subtree
    
    return root;
}
  void Print(TreeNode * d1)//Print
  {
      if(d1==nullptr)
          return;
      Print(d1->left);
      cout<<d1->val<<' ';
       Print(d1->right);
  }
int main()
{
    string d1;
    cin>>d1;
    int i=0;
  Print(Construction(d1,i));
}

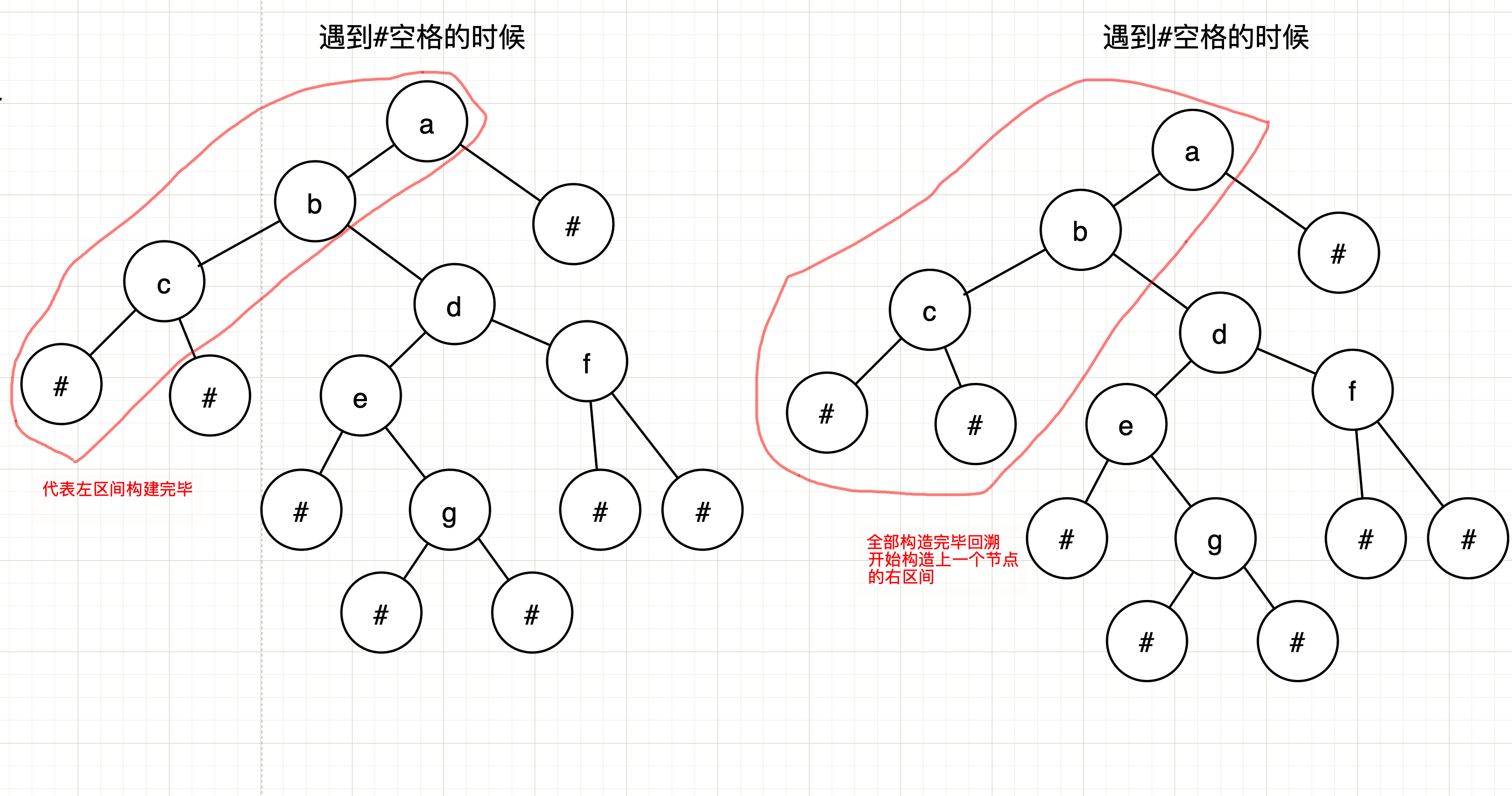
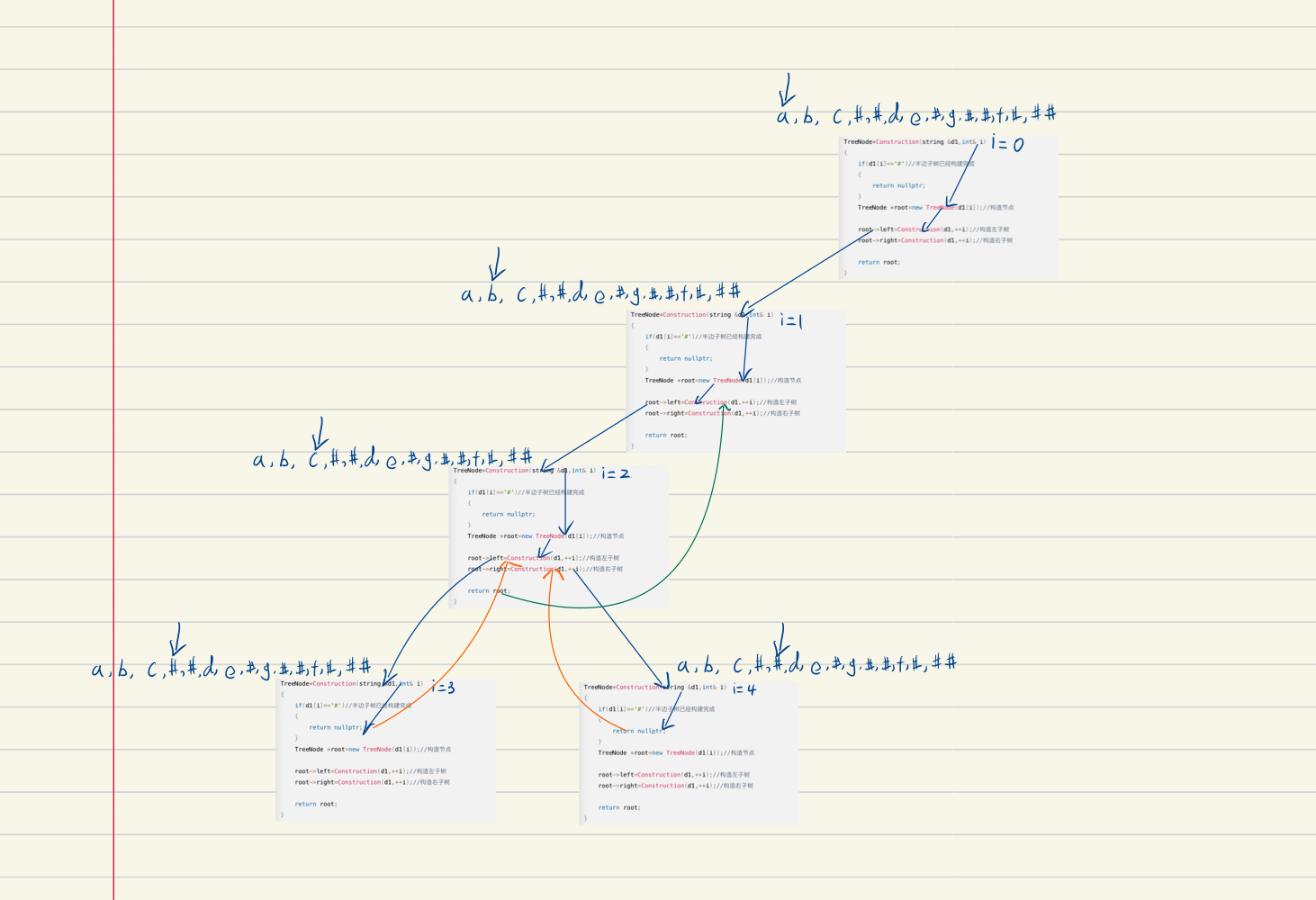
Schematic Construction:

In fact, the idea is very simple, but how does it build? Draw as usual
The blue line represents recursion
The orange line represents: return to the calling position
The green line means: return to the calling position (the node is built)


The same is true for later node construction

The second layer constructs a binary tree given the pre middle order

Title Description: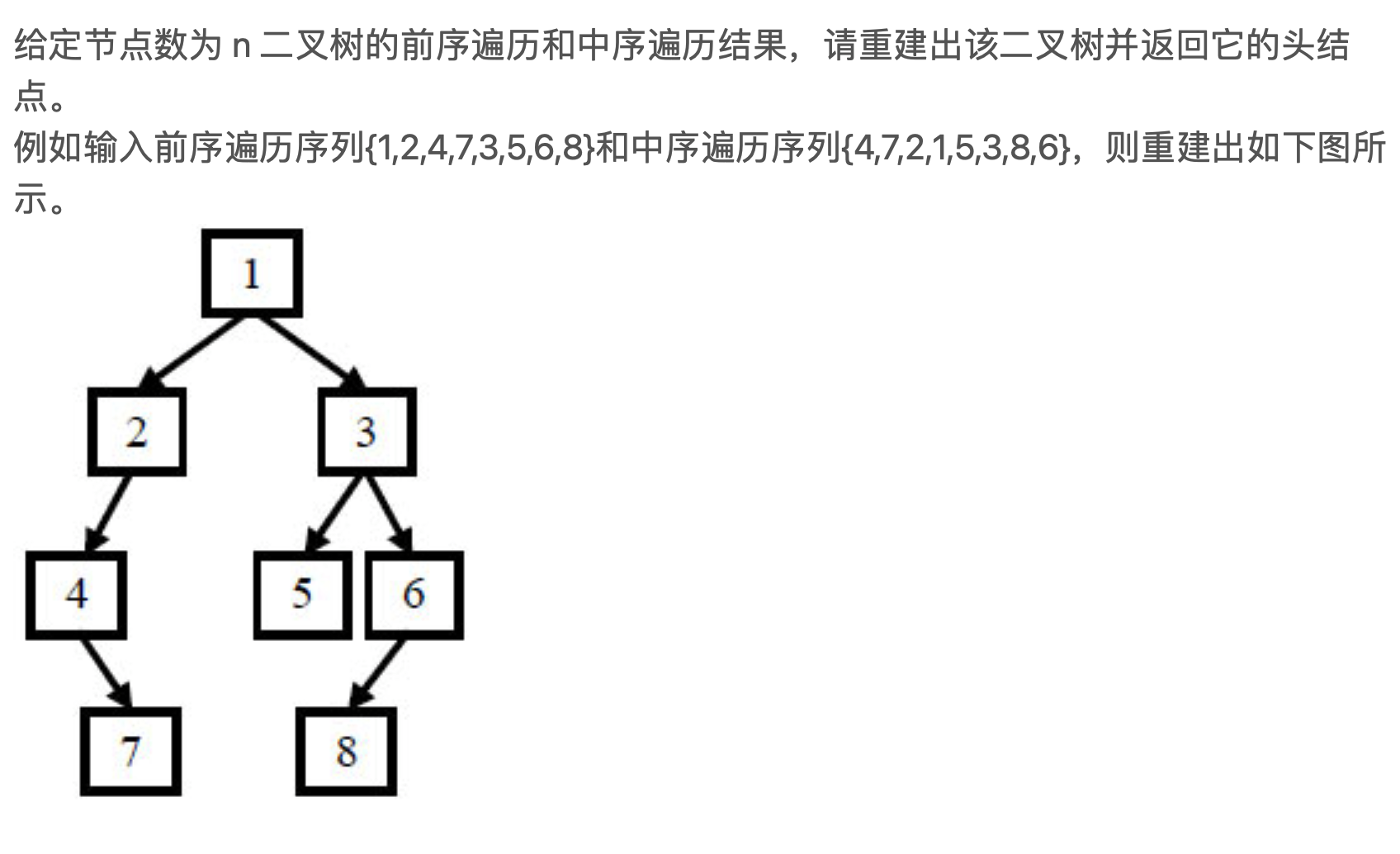

Brief review:

Preorder traversal is rooted in the left subtree and the right subtree
Middle order traversal is to first the left subtree in the root right subtree

Idea:

If the preamble traverses the root every time, we can rely on the preamble to determine the location of the root node, while the middle order traverses the left subtree at the root first, so we can find the root determined by the preamble in the middle order to divide the left and right subtrees. In fact, the idea is two sentences. The preamble finds the root and the middle order divides the left and right subtrees

code:

Step 1:
Carry out special processing, build sub functions and recursively build trees (the original function structure does not meet the requirements of recursive tree building)

 TreeNode* reConstructBinaryTreeHelp(vector<int>& pre,int pre_start,int pre_end,vector<int>& vin,int vin_start,int vin_end)
    {
    
    }
    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin)
    {
        if(pre.size()<vin.size())//The sequence given to you in special cases does not belong to the same tree
        {
            return nullptr;
        }
        
    
       
     return reConstructBinaryTreeHelp(pre,0,pre.size()-1,vin,0,pre.size()-1);//Build a tree and pass the valid intervals of pre and vin. It can also be seen that we pass the closed interval, that is, [0,pre.size()-1] can be accessed using subscripts, and so can vin

Step 2: implement recursive main logic:

 TreeNode* reConstructBinaryTreeHelp(vector<int>& pre,int pre_start,int pre_end,vector<int>& vin,int vin_start,int vin_end)
    {
    
    
      //Recursive end exit
        if(pre_start>pre_end||vin_start>vin_end)//If their start position is greater than their end position, there is no node
        {
            return nullptr;
        }
       TreeNode*root=new TreeNode(pre[pre_start]);//Construct a node. The preamble is the root
    
    
      for(int i=vin_start;i<=vin_end;i++)//If the left and right intervals are divided in the middle order, the starting position must be the start of the middle order, and the end is the end
      {
          if(pre[pre_start]==vin[i])//Find the root in the middle order, divide the left and right subtrees, and start building
          {
              //The left subtree is constructed to control the interval
              root->left=reConstructBinaryTreeHelp(pre, , ,vin, , );
              root->right=reConstructBinaryTreeHelp(pre, , ,vin, , );
              break;//This step shows that the tree has been built
          }
          
      }
      return 0;
    
    }

Step 3: determine the interval:

In fact, the difficult part is not the idea, but the idea is very good, but controlling his interval is the essence of the problem, so we take him out one by one for detailed analysis. Here, we also need to combine the code of dividing the left and right subtree cycle in the second part, but I will draw a picture to indicate it

First division

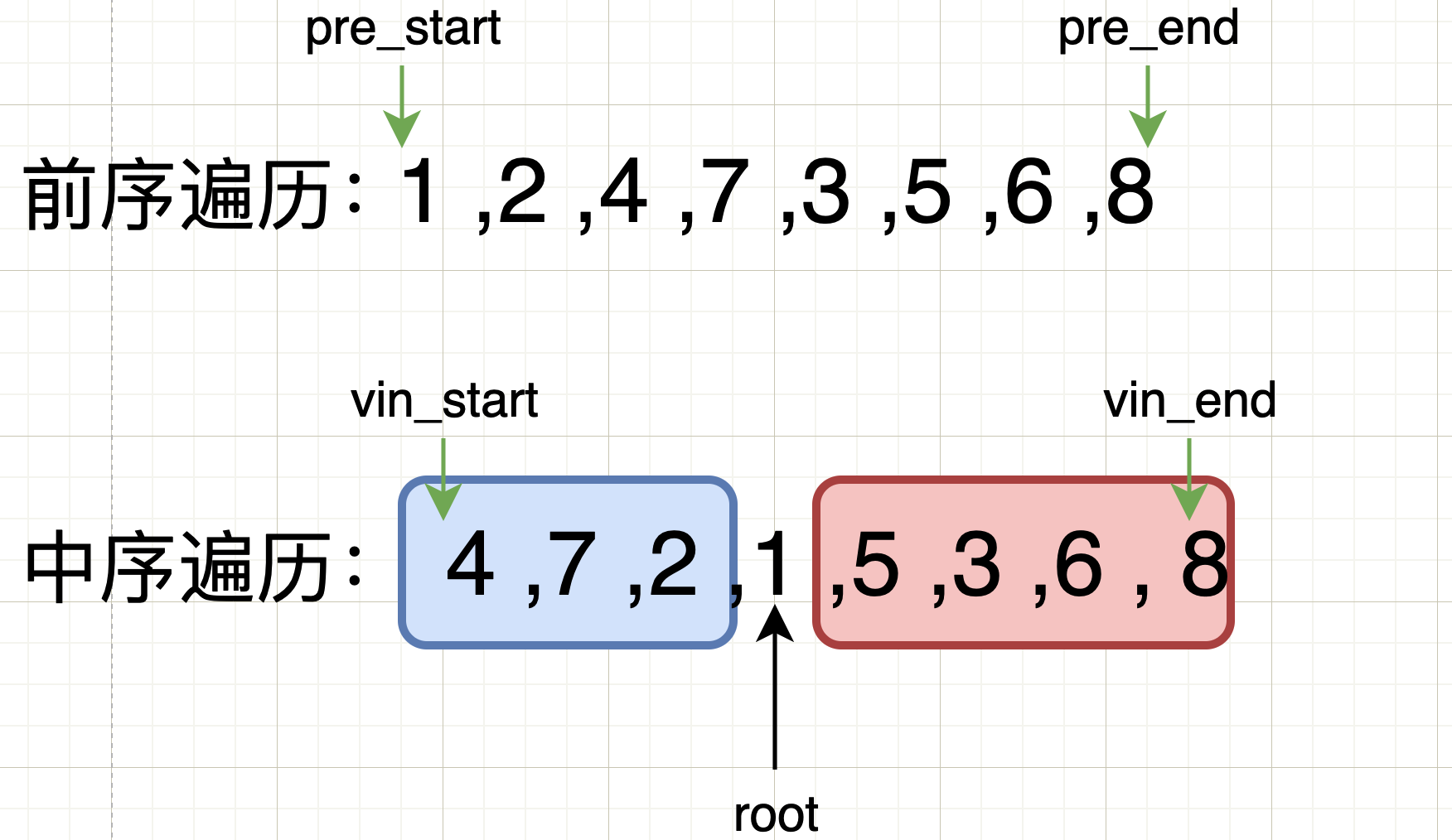
Of left subtree:

pre_start

In the first division, it can be seen that pre_ In fact, start only needs to point to the next position. The preamble determines the root

vin_start

His range is still vin_start is as shown in the first partition

vin_end

The position of end is the previous position of the current root (i-1), then the position of root is I (the second part determines the loop of root position), and the code implementation is a closed interval, as shown in the first division

pre_end

So now let's think about a problem. How do we know the number of nodes of the left subtree in the preamble?


According to the node interval of the preamble shown in the figure is [1,7], how to control it? Now we are thinking about something closely related to the nodes of the left subtree... Oh, the start and end of the middle order traversal point to the interval, which is not the number of nodes of the left subtree? Right


As the above analysis shows_ End = = I-1, then it can be concluded that the interval is pre_start+1 (the starting position of the preamble) + I-1 - vin_start --- > the final interval is pre_start+i-vin_start

Of right subtree:

pre_start

As can be seen from the figure, the right subtree is actually the upper left subtree pre for the preamble_ End + 1 is pre_start+i-vin_start+1

pre_end

His ending position is also very simple, as shown in the figure, still pre_end

vin_start

As can be seen from the figure, the starting position of the interval of the right subtree after segmentation is i (root node), which is i+1

vin_end

His ending position is also very simple, as shown in the figure, still vin_end

code:

     root->left= reConstructBinaryTreeHelp(pre,pre_start+1,  pre_start+i-vin_start       ,vin,vin_start ,i-1);
                root->right=reConstructBinaryTreeHelp(pre,  pre_start+i-vin_start+1           , pre_end,vin,i+1 , vin_end);

Nagging at home

Analyze more. Once you are born, twice you are ripe, and three times you are good friends. Remember to take it out and write it regularly