Today's problem begins to take the postgraduate entrance examination algorithm, and the problem has become much more interesting. The array inversion of the second problem is a very classic example, which is worth pondering carefully.

Sword finger Offer 04. Search in two-dimensional array

In an n* m two-dimensional array, each row is sorted in ascending order from left to right, and each column is sorted in ascending order from top to bottom. Please complete an efficient function, enter such a two-dimensional array and an integer, and judge whether the array contains the integer.

Example:

The existing matrix is as follows:

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Given target = 5, return true.

Given target = 20, false is returned.

Limitations:

0 <= n <= 1000
0 <= m <= 1000

Solution 1 (violence search)

class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        if(matrix.size() == 0)return false;
        int n = matrix.size(), m = matrix[0].size();
        for(int i = 0; i < n; ++ i){
            for(int j = 0; j < m; ++ j){
                if(matrix[i][j] == target){
                    return true;
                }
                if(matrix[i][j] > target){
                    break;
                }
            }
        }
        return false;
    }
};

Algorithm idea:

On the basis of ordinary matrix search, traverse row by row and column by column. Because both rows and columns have monotonicity, if it is found that the element is greater than the target value during traversal, you do not need to continue to query in this row. Due to monotonicity, you can skip this row and directly query in the next row. Although the row increment condition is used, the column increment condition is not used. This solution can pass, but it can continue to optimize.

Solution 2 (optimized into linear search)

class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        if(matrix.size() == 0)return false;
        int n = matrix.size(), m = matrix[0].size();
        if(m == 0)return false;
        int x = 0, y = m - 1;
        while(x < n && y >= 0){
            if(matrix[x][y] == target)return true;
            else if(matrix[x][y] > target)y --;
            else x ++;
        }
        return false;
    }
};

Algorithm idea:

Instead of starting from the upper left corner, start from the upper right corner. If an element is the same, it will return true. If it is greater than the target value, it will move left. If it is less than the target value, it will move down. If one of the x and y coordinates exceeds the boundary, it will return false. The following proves the correctness:

• Shift left (counter evidence): assume that the current traversal position is (x, y), and assume that the target value is at the lower right of the current position (x1, y1), because the traversal process only moves left and down, and the target value is ignored at this time.

  Because (x1, y1) is at the bottom right of (x, y), there are (x1, y) in the same row as (x, y), (x1, y1) in the same column. Matrix [X1] [y] > matrix [x] [y] and matrix [X1] [y] < matrix [X1] [Y1] can be obtained from the topic conditions. When the convenience store arrives at (x1, y), the condition should move down rather than left, so the assumption is not tenable.

• Move down: the same as move left, which can be proved by the method of counter evidence.

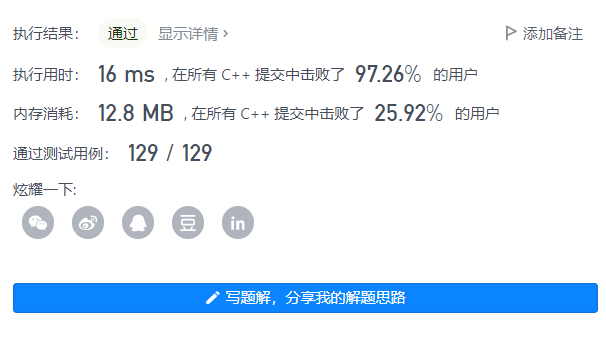
Sword finger Offer 11. Rotate the minimum number of the array

Moving the first elements of an array to the end of the array is called array rotation. Enter a rotation of an incrementally sorted array and output the smallest element of the rotation array. For example, if the array [3,4,5,1,2] is a rotation of [1,2,3,4,5], the minimum value of the array is 1.

Example 1:

Input:[3,4,5,1,2]
Output: 1

Example 2:

Input:[2,2,2,0,1]
Output: 0

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int n = numbers.size(), ans = min(numbers[0], numbers[n - 1]);
        int l = 0, r = n - 1;
        while(l < r){
            int mid = (l + r) / 2;
            if(numbers[mid] < numbers[r]){
                r = mid;
            }else if(numbers[mid] > numbers[r]){
                l = mid + 1;
            }else r --;
        }
        return numbers[l];
    }
};

Algorithm idea:

Invert an ordered sequence into two sequences, and the two sequences are still ordered. We call the two sequences a and B, the first is a and the last is B. A can be empty and B cannot be empty. The main idea of this problem is to shrink the B array by dichotomy to 1 to get the result. Define the head and tail pointers l, r, and get a mid every two points. When numbers [mid] < numbers [R], the mid moves forward to mid in B; When numbers [mid] > numbers [R], mid is in a, and l moves to mid+1; When numbers[mid]==numbers[r], both cases are possible. The solution is to move r forward one bit. The reason is:

• Suppose that at this time, mid moves forward one bit in A: r, assuming that the length of B is only 1 at this time, and the length of r moves forward becomes 0. At this time, it becomes an ordered sequence, and the binary search can still solve the problem; If the length of B is greater than 1, the forward movement of r has no effect on finding the minimum value in B.
• Suppose that at this time, mid moves forward one bit in B: r, and suppose that the length of B is only 1. In this case, only the whole sequence is equal, and the forward movement of r has no effect on the result; If the length of B is greater than 1, the forward movement of r has no effect on finding the minimum value in B.

Therefore, the result can be obtained quickly through the dichotomy method.

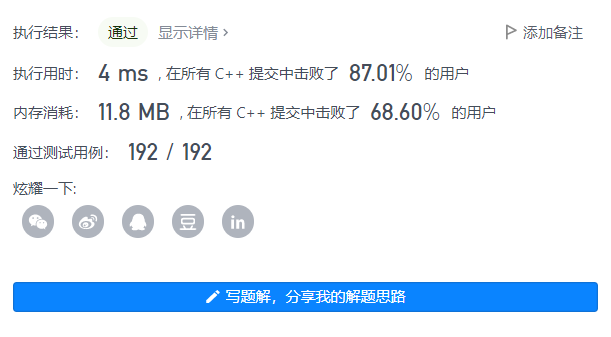
Sword finger Offer 50. The first character that appears only once

Find the first character in the string s that appears only once. If not, a single space is returned. S contains only lowercase letters.

Example 1:

Input: s = "abaccdeff"
Output:'b'

Example 2:

Input: s = "" 
Output:' '

Limitations:

0 <= s Length of <= 50000

class Solution {
public:
    char firstUniqChar(string s) {
        // unordered_map<char, int> mp;
        int mp[26] = {0};
        for(auto w : s){
            mp[w - 'a'] ++;
        }
        for(auto w : s){
            if(mp[w - 'a'] == 1)return w;
        }
        return ' ';
    }
};

Algorithm idea:

This problem is relatively simple. It can be solved directly by hash. Because there are only lowercase letters, it can be stored by opening a 26 size array.

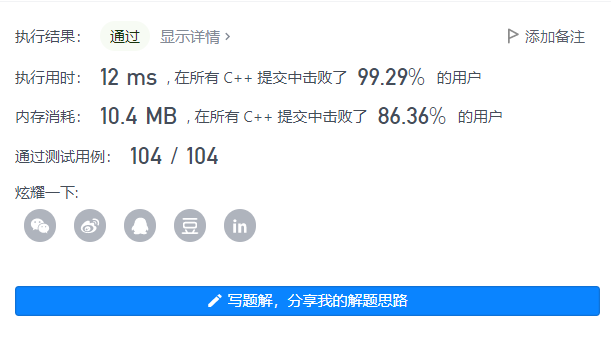
[sword finger Offer] series:
[sword finger Offer] stack
[sword finger Offer] linked list
[sword finger Offer] string
[sword finger Offer] search algorithm