Stack push and stack sequence

Title Description:

Review the basic structure of the stack:

The stack structure is first in first out, last in first out


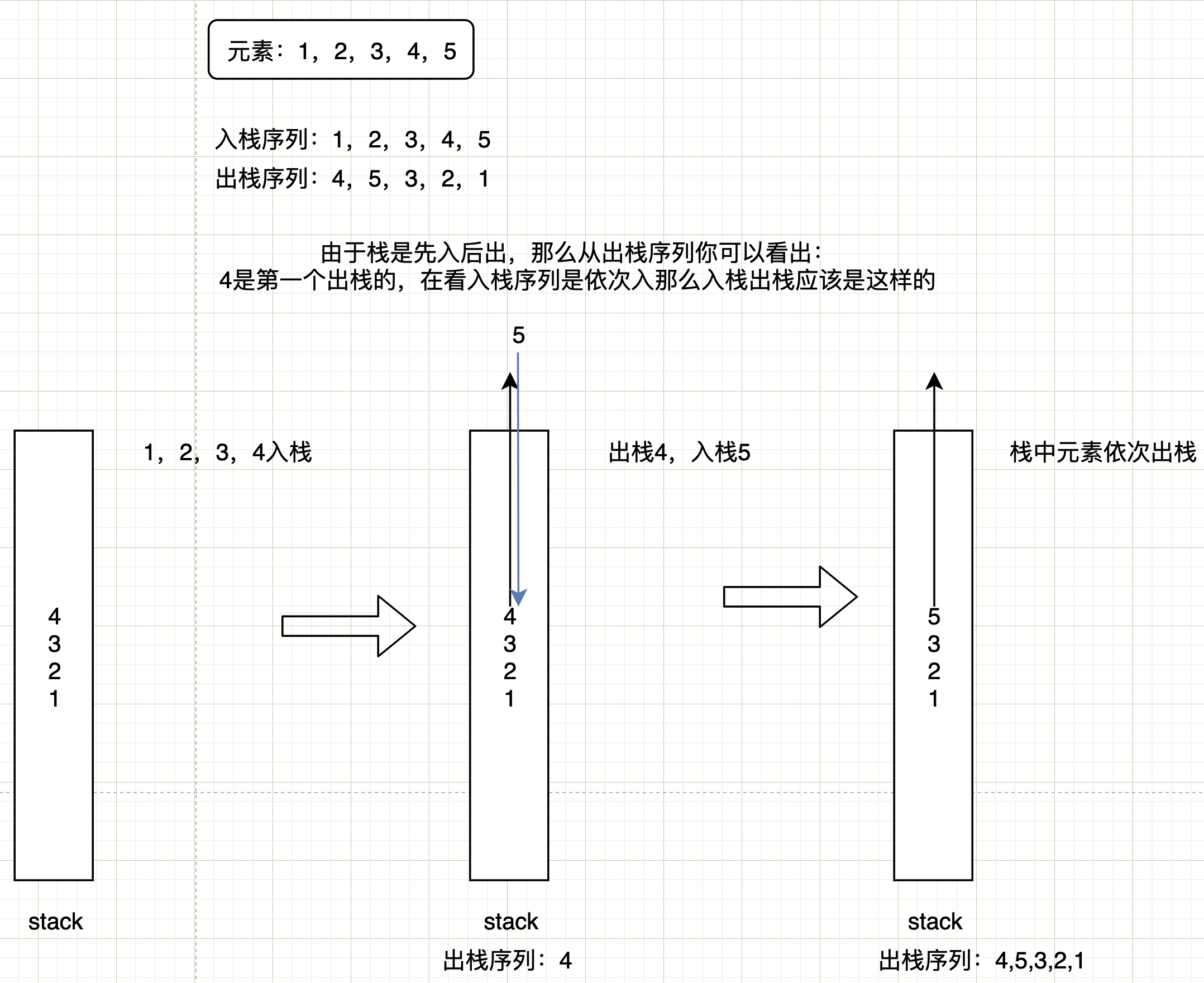
Stack in sequence: [1,2,3,4,5] stack out sequence [4,5,3,2,1], does it belong to the same stack in and out sequence?
There may be hints in the stack:

Idea:

• Use a stack simulation to realize stack entry, and compare whether the element is out of the stack in advance with the out of the stack sequence

code:

    bool IsPopOrder(vector<int> pushV,vector<int> popV)
    {
        if(pushV.size()==0&&popV.size()==0)//exceptional case
        {
            return false;
        }
        int push_index=0,pop_index=0;
        while(push_index<pushV.size())//When there are no elements in the stack sequence, the result should be given, because if the simulation stack and the stack sequence are not matched, it will be false
        {
            st.push(pushV[push_index++]);
            while(!st.empty()&&st.top()==popV[pop_index])//Note that always equal stack may lead to cross-border access due to empty stack
            {
                st.pop();
                pop_index++;
            }
        }
        return st.empty();//Empty means full compliance
    }
    
private:
    stack<int>st;
};

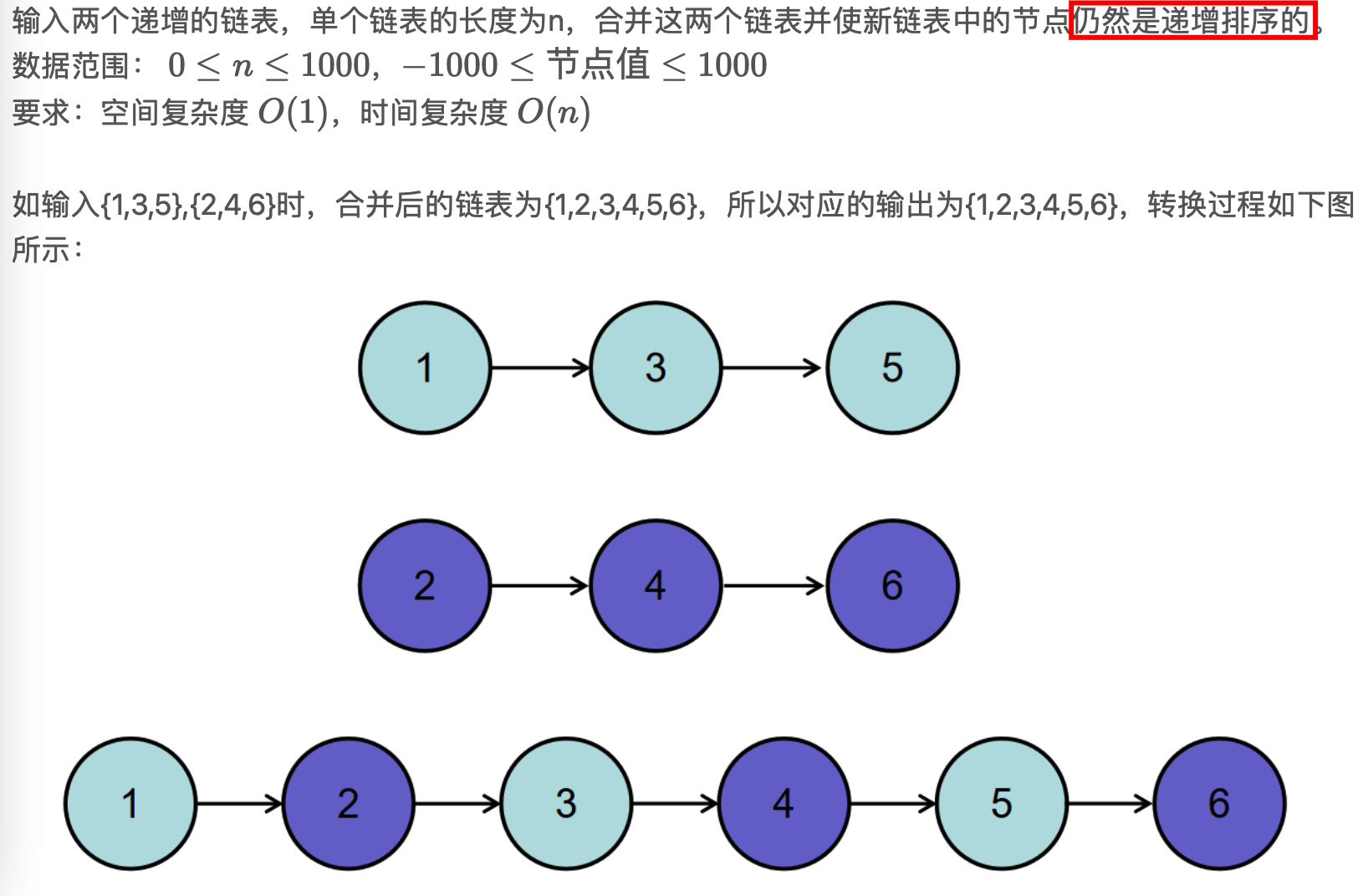
Consolidation of linked lists

Title Description:

Idea:

• Merge and compare size insertion method

Open a new linked list as a container and insert the smaller values into the linked list in turn

code:

  ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
    {
        
        
         //exceptional case
        if(pHead1==nullptr)
        {
            return pHead2;
        }
        if(pHead2==nullptr)
        {
            return pHead1;
        }

        //Open up a new linked list as a container and take the lead in the linked list (sentinel position)
        ListNode* ret=new ListNode(0);
        ListNode* NewHead=ret;
        
        while(pHead1&&pHead2)//Comparing the size requires two linked lists to have values
        {
        
            if(pHead1->val<pHead2->val)//Linked list 1 is smaller than linked list 2
               {
                   ret->next=pHead1;
                   pHead1=pHead1->next;
                   ret=ret->next;
               }
            else//Linked list 2 is smaller than linked list 1
            {
                   ret->next=pHead2;
                   pHead2=pHead2->next;
                   ret=ret->next;
            }            
        }
 
        //exceptional case      
        if(pHead1)//When all nodes of linked list 2 are inserted into the container, linked list 1 also has elements
        {
            ret->next=pHead1;
        }
        if(pHead2)//conversely
        {
            ret->next=pHead2;
       }
       
        return NewHead->next;//Return linked list
    }

• Recursive comparison method

Additional description and explanation of sentinel position and lead linked list

This node is not the element in the linked list. Its function is to delete the element of a node conveniently. You can regard it as the old hen in the game of Eagle catching chicken

Postorder traversal sequence of binary search tree

Title Description:

Knowledge supply:

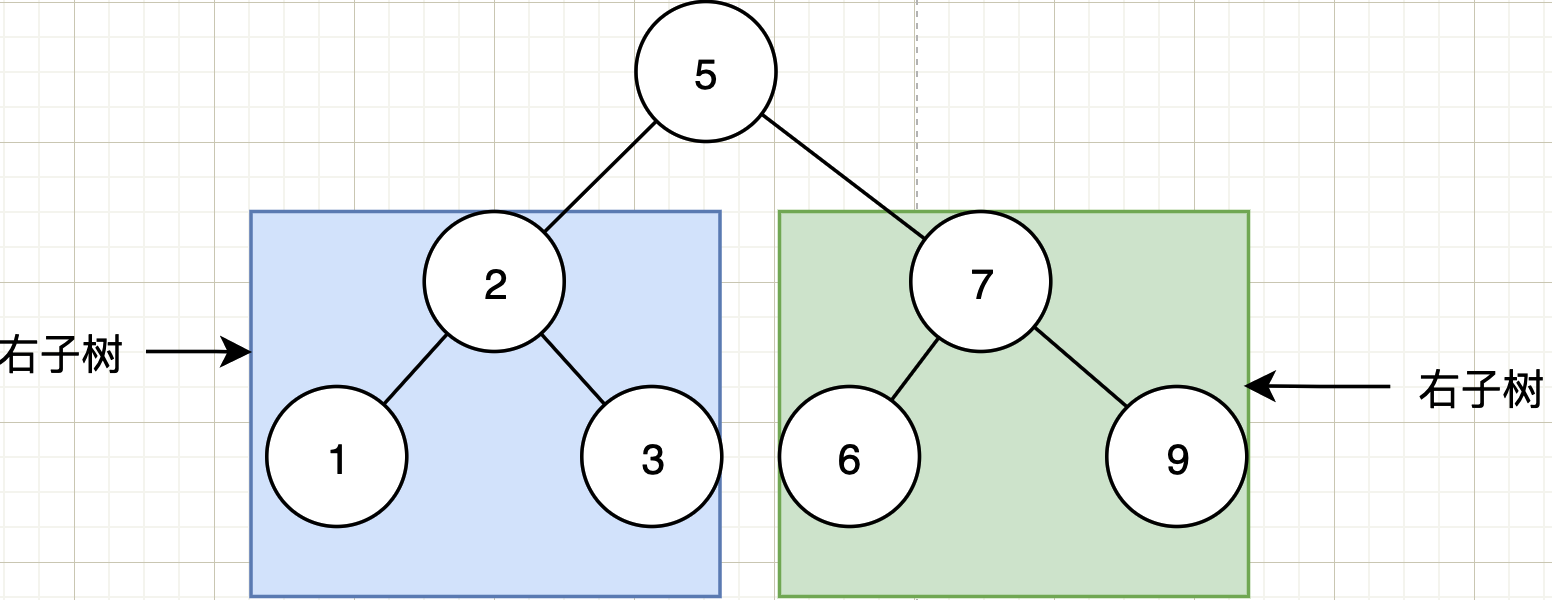
Binary search tree
The left subtree is always greater than the root node, and the right subtree is always greater than the root node
As shown in the figure:



Subsequent traversal:
The subsequent traversal of the binary search tree in the above figure is as follows:
1->3->2->6->9->7->5

Idea:

In the knowledge supply, we can see that the characteristic of binary search tree is that the left subtree is larger than the root node and the right subtree is larger than the root node. Then we only need to find the root to judge whether the left subtree is smaller than the root node and whether the right subtree is larger than the root node

So now there is a problem is how to find the root?

It is still in the knowledge supply. The subsequent traversal first traverses the left subtree, then the right subtree, and then the root. Then the last node of the subsequent traversal is the root of the tree (if you are confused, see the knowledge supply or this article before you) Binary tree Foundation)

Code implementation:

Main logic

    bool VerifySquenceOfBST(vector<int> sequence) 
    {
        
        if(sequence.empty())//Special treatment, beware of fraud
        {
            return false;
        }        
        
         return VerifySquenceOfBSTHelp(sequence,0,sequence.size()-1);//Recursive start judgment
    }

Judgment part

    bool VerifySquenceOfBSTHelp(vector<int>& sq,int start,int end)
    {
        if(start>=end)//When you have only one and element, it means that there is no element to judge in comparison
        {
            return true;
        }
        
        int root=sq[end];//The last element of the sequence is the root
        
        //Partition interval
        int i; 
        for(i =start; i<end;i++)//end is the root, so less than once
        {
            if(sq[i]>root)//If it is larger than the root, it means that i is already a right subtree
            {
                break;
            }
        }
        
        for(int j =i;j<end;j++)//Right subtree
        {
            if(sq[j]<root)//If a node in the right subtree interval is less than the root, it is not a binary search tree
            {
                return false;   
            }
        }
        
        
        //recursion
        return  VerifySquenceOfBSTHelp(sq, , )&&VerifySquenceOfBSTHelp(sq, , )    
    }

interval analysis

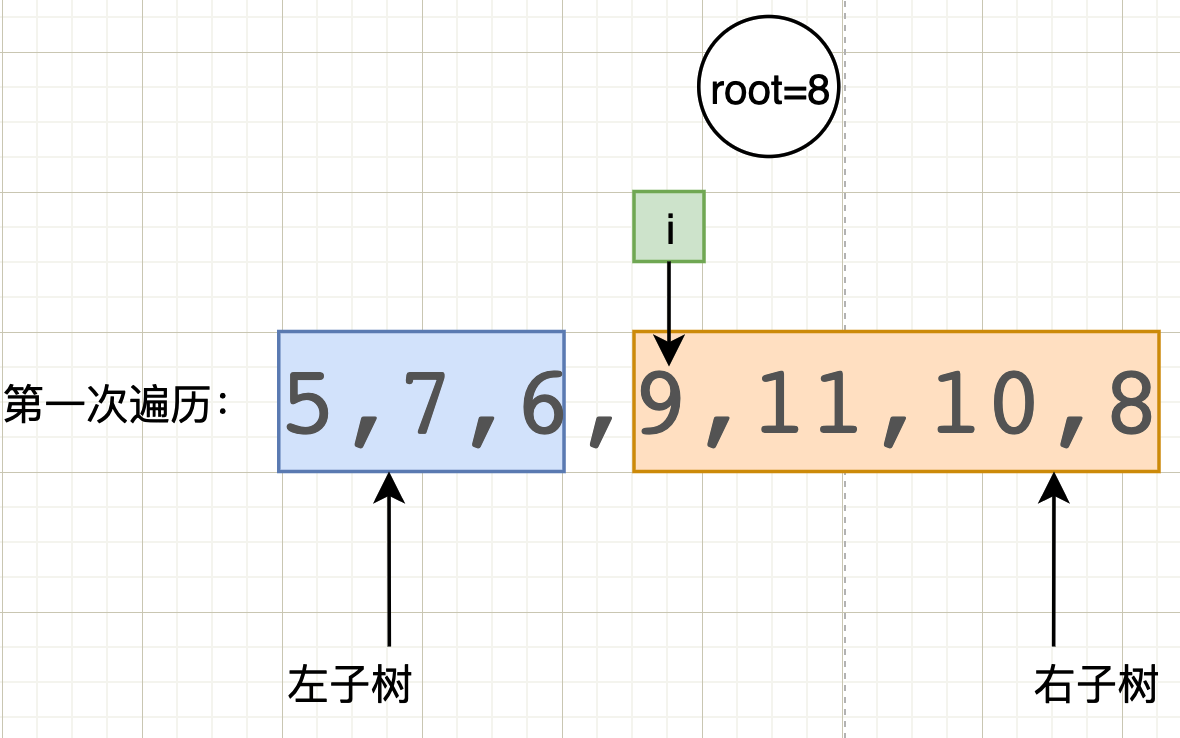
First traversal:

Left subtree start

From the first traversal, we can see that the start of the left subtree is still the starting position of the sequence, that is, the start of the current node

Left subtree end

From the first traversal, it can be found that the end of the left subtree is the previous position of i, so the end of the left subtree is i-1

Right subtree start

From the first traversal, we can find that the start of the right subtree is actually the current position of i, so the start of the left subtree is i

Right subtree end

After the first traversal, the current root node is no longer useful to us, so the end of the right subtree is the current end-1

return  VerifySquenceOfBSTHelp(sq,start ,i-1 )&&VerifySquenceOfBSTHelp(sq,i ,end-1 );

Title Link

First question
Second question
Question 3

Nagging at home

The weather is a little cold recently. Please keep warm. Today happens to be January 1, 2022. I wish you a happy new year, a new atmosphere in the new year, get rid of your bad habits and keep the good habits of last year